Біномний розподіл

Розподіл Бернуллі

Деякі дискретні розподіли

Випадкова величина Х має розподіл Бернулі з параметром , якщо

хі
рі	1– р	р

Її математичне сподівання і дисперсія відповідно дорівнюють:

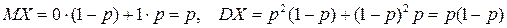
Розподіл Бернуллі відіграє фундаментальну роль в теорії ймовірностей, оскільки він є моделлю будь-якого випадкового експерименту, виходами якого є дві протилежні події.

Нехай проводиться п випробувань з можливими виходами А або в кожному випробуванні, причому подія А має сталу ймовірність р появи в одній спробі (схема Бернуллі). Позначимо . Тоді ймовірність появи події А k раз в п спробах дорівнює:

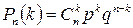. (ІІ.13)

Розподіл випадкової величини Х, яка дорівнює кількості появи події А в п випробуваннях називається біномним розподілом. Випадкову величину Х можна розглядати як суму , де 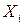— випадкова величина з розподілом Бернулі, яка характеризує появу події А в і– ому випробуванні. Тому математичне сподівання, дисперсія та середнє квадратичне відхилення розподіленої за біномним розподілом випадкової величини дорівнюють:

(ІІ.14)

Приклад 10. Імовірність народження хлопчика дорівнює 0,52. Записати розподіл кількості хлопчиків серед 10 новонароджених та знайти його числові характеристики.

Розв’язання: Значення ймовірностей для кожного значення випадкової величини, знаходимо за формулою (ІІ.13). Ввівши команду Maple:

p:=0.52;q:=1-p;seq(binomial(10,i)*p^i*q^(10-i),i=0..10);,

отримаємо шуканий розподіл:

х
р	0,0007	0,0070	0,0343	0,0991	0,1878	0,2441	0,2204	0,1364	0,0554	0,0133	0,0015

Графічно його можна зобразити таким чином:

Рис. 6.

На основі формул (2.14) отримуємо МХ= 5,2, DX= 2,496, σ X» 1,58.

Функцію розподілу даної випадкової величини можна задати у вигляді таблиці:

х	x £0	0 <x £1	1 <x £2	2 <x £3	3 <x £4	4 <x £5	5 <x £6	6 <x £7	7 <x £8	8 <x £9	9 <x £10	x> 10
F (x)		0,0007	0,0077	0,042	0,1411	0,3289	0,573	0,7934	0,9298	0,9852	0,9985

Отже, медіаною розподілу цієї випадкової величини є точка т = x_½= 5, а квартилями — точки x_¼= 4 та x_¾= 6.

Дата добавления: 2015-05-23