Функція розподілу двовимірної випадкової величини

Двовимірна випадкова величина

Розподіл Фішера-Снедекора

k ₁ = 5, k ₂ = 7

k ₁ = 3, k ₂ = 5

k ₁ = 2, k ₂ = 3

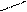
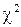Якщо U i V — незалежні випадкові величини, що мають розподіл з k ₁ і k ₂ степенями вільності відповідно, то величина

Рис. 10

має розподіл Фішера-Снедекора з k ₁, k ₂ степенями вільності (рис. 10).

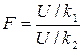
Якщо на одному імовірнісному просторі задано дві випадкові величини (або п випадкових величин), то їх упорядковану пару (Х ₁, Х ₂) (впорядковану сукупність (Х ₁, Х ₂,..., Х_п)) називають двовимірною (п – вимірною) випадковою величиною або двовимірним (п – вимірним) випадковим вектором. Надалі в основному розглядатимемо саме двовимірний випадковий вектор.

Якщо випадкові величини Х ₁, Х ₂ — неперервні, то вектор (Х ₁, Х ₂) називають неперервним випадковим вектором. Коли ж Х ₁, Х ₂ — дискретні випадкові величини, то й вектор (Х ₁, Х ₂) називають дискретним.

Розподіл двовимірного дискретного випадкового вектора можна задати у вигляді таблиці:

X Y	x 1	x 2	…	хі	…	хn
у 1	p 11	p 21	…	pi 1	…	pn 1
…	…	…	…	…	…	…
уj	p 1 j	p 2 j	…	pij	…	pnj
…	…	…	…	…	…	…
уm	p 1 m	p 2 m	…	pim	…	pnm

Тут 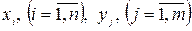значення відповідно випадкових величин Х і Y, а . Зрозуміло, що .

Функція називається функцією розподілу ймовірностей двовимірної випадкової величини. Наприклад, якщо випадковий вектор заданий розподілом

X Y
	0,03	0,5	0,2
	0,15	0,1	0,02

то функція розподілу випадкового вектора матиме вигляд

Функція розподілу ймовірностей двовимірного випадкового вектора має такі властивості.

1. Значення функції розподілу змінюються в межах .

2. Функція розподілу монотонно неспадна за кожним аргументом, тобто:

,

.

3. Імовірність попадання значень випадкової величини в прямокутник обчислюється за формулою

.

4. Справджуються рівності:

.

5. Границею функції розподілу ймовірностей, коли одна із змінних прямує до , є функція розподілу другої змінної:

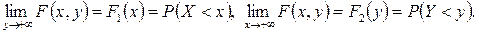
6. За кожним своїм аргументом функція розподілу F є неперервною зліва в будь-якій точці своєї області визначення, тобто

Якщо випадковий вектор 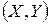є неперервним, то функція неперервна на всій області визначення.

Функцію

,

(якщо вона існує) називають щільністю розподілу ймовірностей двовимірної випадкової величини.

Наприклад, функція є щільністю розподілу неперервної двовимірної випадкової величини, заданої функцією розподілу

Щільність розподілу неперервної випадкової величини має такі властивості:

1. Щільність розподілу завжди невід’ємна .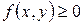

2. Функція розподілу неперервної випадкової величини 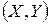визна­ча­єть­ся через щільність її розподілу за формулою

3. Має місце умова нормування .

4. Імовірність попадання значень неперервної випадкової величини в задану область D обчислюється за формулою

.

5. Функції

і

задають щільності розподілів одновимірних неперервних випадкових величин X і Y відповідно.

Дата добавления: 2015-05-23