
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Нерівність Чебишева
|
|
|
|
Граничні закони теорії ймовірностей
Якщо випадкова величина має математичне сподівання М і середнє квадратичне відхилення σ, тоді для довільного  має місце нерівність
має місце нерівність
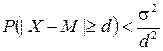 (ІІ.31)
(ІІ.31)
Нерівність (ІІ.31) називають нерівністю Чебишева. Вона дозволяє оцінити імовірність великого відхилення значення випадкової величини від свого математичного сподівання. Разом з нею розглядають нерівність
 ,(ІІ.32)
,(ІІ.32)
яка дозволяє оцінити ймовірність протилежної події.
Доведемо нерівність (ІІ.31). Дійсно, для дискретно розподіленої випадкової величини маємо

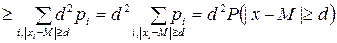 . Звідки
. Звідки 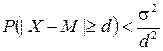 .
.
Для неперервно розподіленої випадкової величини маємо


 . Звідки
. Звідки 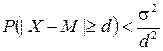 , що і треба було довести.
, що і треба було довести.
Зауважимо, що нерівність Чебишева не передбачає інформації про характер розподілу випадкової величини. Якщо ж відомий розподіл випадкової величини, то можна не тільки оцінити, але й визначити імовірність відхилення випадкової величини від свого математичного сподівання більше, ніж на задану величину.
|
|
|
|
|
Дата добавления: 2015-05-23; Просмотров: 1232; Нарушение авторских прав?; Мы поможем в написании вашей работы!