Коваріаційна матриця і матриця парних кореляцій

Коваріаційною матрицею п -вимірного випадкового вектора називатимемо квадратну матрицю розмір­нос­ті п, елементами якої є парні коваріації компонент випадкового вектора Х. Коваріаційна матриця є симетричною (оскільки 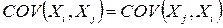), а еле­мен­та­ми головної діагоналі є дисперсії відповідних компонент випадкового вектора. Дійсно .

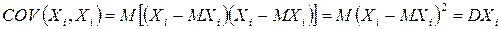У попередньому прикладі коваріаційна матриця має вигляд

.

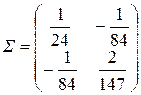Оскільки коваріація двох незалежних компонент вектора дорівнює нулю, то коваріаційна матриця відображає структуру залежності компонент випадкового вектора Х. Зокрема, якщо всі компоненти випадкового вектора стохастично незалежні, то коваріаційна матриця діагональна.

Матрицю 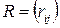, складену з коефіцієнтів лінійної кореляції компонент 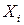та 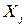випадкового вектора Х, називають матрицею парних кореляцій або кореляційною матрицею. Як і коваріаційна матриця, вона є симетричною. Діагональні елементи кореляційної матриці дорівнюють 1. Кореляційна матриця випадкового вектора з незалежними компонентами є одиничною.

У попередньому прикладі матриця парних кореляцій має вигляд

.

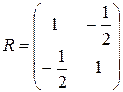Коваріаційна матриця пов’язана з матрицею парних кореляцій співвідношенням

,

де — діагональна матриця, елементами головної діагоналі якої є середні ква­дра­тичні відхилення відповідних компонент випадкового вектора. Зокрема, якщо компоненти вектора мають одиничні дисперсії, то 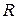і 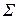збігаються.

Вправа. Переконайтесь в істинності останнього співвідношення для наведених коваріаційної і кореляційної матриць.

Дата добавления: 2015-05-23