Коваріація і коефіцієнт кореляції

Коваріацією (або кореляційним моментом) двовимірної випадкової величини 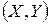називають математичне сподівання добутку відхилень кожної з компонент від свого математичного сподівання

.

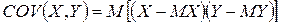Зокрема для дискретного випадкового вектора

або

,

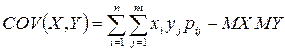а для неперервного

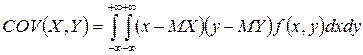
або

.

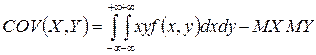Оскільки математичне сподівання добутку двох незалежних випадкових величин дорівнює добутку їх математичних сподівань, то коваріація вектора з незалежними компонентами дорівнює нулю. Отже, якщо коваріація випадкового вектора відмінна від нуля, то його компоненти є стохастично залежними випадковими величинами (обернене твердження не справджується).

Коваріацію можна розглядати як міру залежності випадкових величин, які є компонентами вектора, однак вона враховує не тільки рівень залежності величин, а й їх розсіювання навколо точки 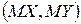на площині. Тому залежність між компонентами двовимірного випадкового вектора характеризують безрозмірною величиною

,

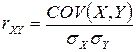яку називають коефіцієнтом лінійної кореляції.

Очевидно, що коефіцієнт лінійної кореляції незалежних випадкових величин дорівнює нулю.

Дві випадкові величини називають некорельованими, якщо їх коефіцієнт лінійної кореляції дорівнює нулю і корельованими у протилежному випадку. Незалежні випадкові величини завжди некорельовані. Обернене твердження не справджується. Однак для нормально розподілених випадкових величин некорельованість рівнозначна стохастичній незалежності.

Покажемо, що

.

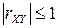Оскільки дисперсія випадкової величини 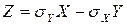невід’ємна, то

.

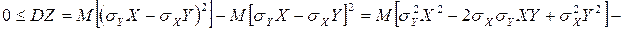
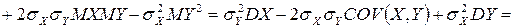
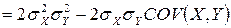Тому

.

Аналогічно доводять, що

,

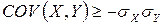розглянувши випадкову величину 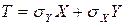, і тому

,

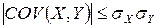що й треба було довести.

На відміну від коваріації, коефіцієнт лінійної кореляції не залежить від ступеня розсіювання випадкових величин і характеризує лише міру їх залежності. Зокрема, якщо 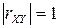, то величини і 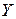— лінійно залежні.

Наведемо приклад знаходження в пакеті Maple коефіцієнта лінійної кореляції двовимірної випадкової величини.

Приклад 14. Знайти коефіцієнт лінійної кореляції компонент вектора, заданого щільністю

.

Розв’язання: Задаємо щільність розподілу випадкового вектора (X, Y):

> restart:f:=(x,y)->14/Pi*sqrt(3)*exp(-16*x^2-28*x*y-49*y^2);

Знаходимо щiльності розподілів випадкових величин Х і Y:

> f1:=x->int(f(x,y),y=-infinity..infinity);f1(x);

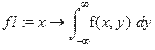
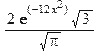
> f2:=y->int(f(x,y),x=-infinity..infinity);f2(y);

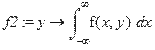
Обчислюємо математичні сподівання, дисперсії та середньоквадратичні їх відхилення:

> m1:=int(x*f1(x),x=-infinity..infinity);D1:=int(x^2*f1(x),x=-infinity..infinity)-m1^2;sigma1:=sqrt(D1);

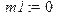
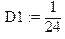
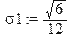
> m2:=int(y*f2(y),y=-infinity..infinity);D2:=int(y^2*f2(y),y=-infinity..infinity)-m2^2;sigma2:=sqrt(D2);

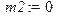
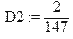
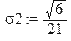
Обчислюємо коваріацію випадкового вектора:

> COV(X,Y):=int(int(x*y*f(x,y),x=-infinity..infinity),y=-infinity..infinity)-m1*m2;

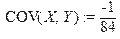
та коефіцієнт лінійної кореляції:

> r(X,Y):=COV(X,Y)/sigma1/sigma2;

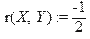
Як бачимо, коефіцієнт лінійної кореляції дорівнює .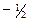

Дата добавления: 2015-05-23