Дисперсія та стандартне відхилення випадкової величини. Асиметрія і ексцес

Дисперсією випадкової величини називається математичне сподівання квадрата відхилення випадкової величини від свого математичного сподівання.

Отже, для обчислення дисперсії дискретно розподіленої випадкової величини маємо формулу

, (ІІ.9)

а для обчислення дисперсії неперервно розподіленої випадкової величини, щільність розподілу якої дорівнює 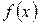, — формулу

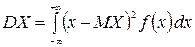. (ІІ.10)

Величина називається середнім квадратичним (або стандартним) відхиленням випадкової величини Х.

Приклад 9. Знайти дисперсію та середнє квадратичне відхилення випадкових величин з прикладів 7 і 8.

Розв’язання: Використовуючи формулу (ІІ.9) та знайдене у прикладі 7 значення математичного сподівання, для дисперсії кількості очок, що випадають при киданні грального кубика, отримуємо

.

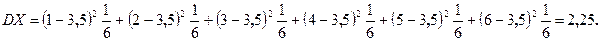
Для неперервно розподіленої випадкової величини з прикладу 8 маємо

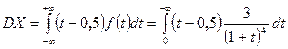. Виконавши команду Maple: int(3*(t-1/2)^2 /(t+1)^4,t=0..infinity);, отримаємо DX = 0,75, а .

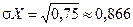Дисперсія випадкової величини має такі властивості.

1. Дисперсія сталої величини дорівнює 0.

2. Сталий множник можна виносити в квадраті за знак дисперсії

D (cX) = c ² DX.

3. Дисперсія суми двох незалежних випадкових величин дорівнює сумі їх дисперсій.

4. Дисперсія випадкової величини дорівнює різниці математичного сподівання квадрата випадкової величини і квадрата її математичного сподівання

.

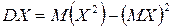Дійсно, .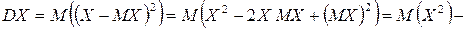

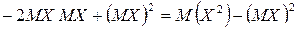Випадкова величина 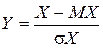називається нормованою випадковою величиною. Її математичне сподівання 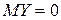, а дисперсія .

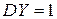Числа

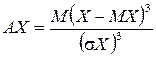(ІІ.11)

та

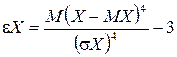(ІІ.12)

називаються відповідно асиметрією та ексцесом випадкової величини Х.

Зауважимо, що математичне сподівання, дисперсія, середньоквадратичне відхилення, асиметрія, ексцес випадкової величини існують не завжди. Наприклад, для випадкової величини із щільністю 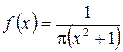жодна з цих величин не існує.

Дата добавления: 2015-05-23