Поняття випадкової величини

ІІ. Випадкова величина

Доволі часто результатам випробування можна поставити у відповідність певні числові значення. Числову функцію задану на деякому імовірнісному просторі називають випадковою величиною. Випадкова величина породжує імовірнісний простір, елементами якого є значення або множини значень цієї випадкової величини, які утворюють певну σ-алгебру, і які можуть набуватися з певною ймовірністю.

Наприклад, при киданні грального кубика може випасти 1, 2, 3, 4, 5 або 6 очок. Імовірність кожної з цих подій дорівнює 1/6. Даний експеримент описується випадковою величиною, яка може набувати значень 1, 2, 3, 4, 5 або 6 з однаковими ймовірностями 1/6.

Випадкові величини поділяють на неперервні і дискретні. Розглянута в попередньому прикладі величина є дискретною випадковою величиною. Дискретна випадкова величина може набувати лише певних окремих значень із заданими ймовірностями. Дискретними випадковими величинами є, наприклад, кількість хлопчиків на 1000 новонароджених, кількість абонентських з’єднань на АТС протягом доби, кількість завдань тесту виконаних досліджуваним за певний проміжок часу. Неперервна випадкова величина може набувати будь-яких значень з певного інтервалу числової прямої чи об’єднання інтервалів із заданими ймовірностями. Прикладом неперервної випадкової величини може служити тривалість очікування автобуса на зупинці, час з моменту подразнення до появи реакції досліджуваного на подразник, кутова величина поля зору людини і т.п. Очевидно, що неперервна випадкова величина може набувати незлічену кількість значень, і тому ми можемо говорити лише про імовірність потрапляння цих значень в деякий інтервал, а не про ймовірність набуття неперервною випадковою величиною конкретного значення (вона завжди дорівнює нулеві).

Поряд із розглянутими вище скалярними випадковими величинами доводиться мати справу з векторнимивипадковимивеличинами. Випадковим вектором або векторною випадковою величиною будемо називати будь-­яку впо­ряд­ко­ва­ну сукупність скалярних випадкових величин. Так результат опитування людини за опитувальником 16PF Кеттела можна розглядати як 16-ти вимірний дискретний випадковий вектор.

Розподілом випадкової величини називатимемо розподіл імовірностей значень випадкової величини у відповідному імовірнісному просторі.

Випадкові величини будемо позначати великими буквами, наприклад, X, Y, Z, а їх значення малими буквами x, y, z.

Приклад 1. Розподіл двовимірної випадкової величини задано таблицею

Y X	-1

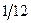
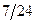
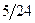
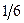
Знайти розподіл випадкової величини Z=XY.

Розв’язання: Випадкова величина Z може набувати значень –2, 0 або 2. Значення –2 вона набуватиме, якщо величина набуває значення (2,–1), значення 2 набуватиме,якщо величина набуває значення (2, 1), у всіх інших випадках вона набуватиме значення 0. Отже, , , 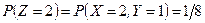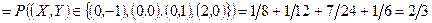. Розподіл випадкової величини Z має вигляд:

	–2

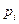
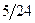
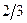
Дата добавления: 2015-05-23