
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Поняття матриці. Операції над матрицями
|
|
|
|
Матриці, визначники, системи лінійних рівнянь
Д о д а т о к 2: Елементи вищої математики
Критичні значення рангового коефіцієнта кореляції Спірмена
Критичні значення критерію Пейджа
| k | p | ||||
| п | |||||
| 0,01 | |||||
| 0,05 | |||||
| 0,01 | |||||
| 0,05 | |||||
| 0,01 | |||||
| 0,05 | |||||
| 0,01 | |||||
| 0,05 | |||||
| 0,01 | |||||
| 0,05 | |||||
| $63 | 0,01 | ||||
| 0,05 | |||||
| 0,01 | |||||
| 0,05 | |||||
| 0,01 | |||||
| 0,05 | |||||
| 0,01 | |||||
| 0,05 | |||||
| 0,01 | |||||
| 0,05 | |||||
| 0,01 | |||||
| 0,05 |
Таблиця 14
| n | p | n | p | n | p | |||
| 0,05 | 0,01 | 0,05 | 0,01 | 0,05 | 0,01 | |||
| 0,94 | — | 0,48 | 0,62 | 0,37 | 0,48 | |||
| 0,85 | — | 0,47 | 0,6 | 0,36 | 0,47 | |||
| 0,78 | 0,94 | 0,46 | 0,58 | 0,36 | 0,46 | |||
| 0,72 | 0,88 | 0,45 | 0,57 | 0,36 | 0,45 | |||
| 0,68 | 0,83 | 0,44 | 0,56 | 0,34 | 0,45 | |||
| 0,64 | 0,79 | 0,43 | 0,54 | 0,34 | 0,44 | |||
| 0,61 | 0,76 | 0,42 | 0,53 | 0,33 | 0,43 | |||
| 0,58 | 0,73 | 0,41 | 0,52 | 0,33 | 0,43 | |||
| 0,56 | 0,70 | 0,49 | 0,51 | 0,33 | 0,43 | |||
| 0,54 | 0,68 | 0,39 | 0,50 | 0,32 | 0,41 | |||
| 0,52 | 0,66 | 0,38 | 0,49 | 0,32 | 0,41 | |||
| 0,50 | 0,64 | 0,38 | 0,48 | 0,31 | 0,4 |
Матрицею розмірності m ´ n називають прямокутну таблицю чисел, яка складається з m рядків і п стовпчиків. Числа, які утворюють матрицю називають елементами матриці. Матриці позначають великими літерами латинського алфавіту, а їх елементи відповідними малими літерами з індексами. Наприклад,
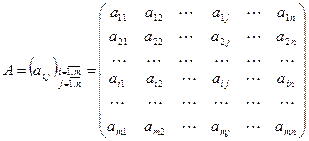 .
.
Дві матриці називаються рівними, якщо вони мають однакову розмірність і їх відповідні елементи рівні.  .
.
Матриця, яка складається з одного рядка (одного стовпчика) називається вектор-рядком (вектор-стовпчиком). Як правило замість  або
або  відповідно пишуть
відповідно пишуть 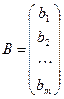 та
та 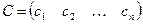 .
.
Квадратною матрицею п- го порядку називається матриця, яка складається з п рядків і п стовпчиків. Наприклад,  — квадратна матриця 2-го порядку. Квадратна матриця, всі елементи якої дорівнюють нулеві, називається
— квадратна матриця 2-го порядку. Квадратна матриця, всі елементи якої дорівнюють нулеві, називається
нуль-матрицею.
Елементи  квадратної матриці п- го порядку називаються діагональними і утворюють головну діагональ матриці. Матриця, всі елементи якої окрім діагональних дорівнюють нулеві, називається діагональною. Діагональну матрицю, у якої всі діагональні елементи дорівнюють одиниці, називають одиничною і позначають буквою Е.
квадратної матриці п- го порядку називаються діагональними і утворюють головну діагональ матриці. Матриця, всі елементи якої окрім діагональних дорівнюють нулеві, називається діагональною. Діагональну матрицю, у якої всі діагональні елементи дорівнюють одиниці, називають одиничною і позначають буквою Е.
Добутком матриці 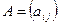 на число lназиватимемо матрицю
на число lназиватимемо матрицю  , кожен елемент якої дорівнює відповідному елементу матриці А, помноженому на скаляр l. Наприклад, якщо
, кожен елемент якої дорівнює відповідному елементу матриці А, помноженому на скаляр l. Наприклад, якщо  , то
, то  . Матрицю – А=– 1× А називають протилежною до матриці А.
. Матрицю – А=– 1× А називають протилежною до матриці А.
Сумою матриць 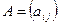 і
і  однакової розмірності називають матрицю
однакової розмірності називають матрицю 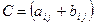 , кожен елемент якої дорівнює сумі відповідних елементів матриць А і В. Наприклад, якщо
, кожен елемент якої дорівнює сумі відповідних елементів матриць А і В. Наприклад, якщо  , а
, а  , то
, то  .
.
Добутком матриці 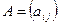 розмірності т ´ п на матрицю
розмірності т ´ п на матрицю 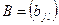 розмірності п ´ р називають матрицю
розмірності п ´ р називають матрицю 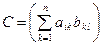 розмірності т ´ р, кожен елемент якої є сумою добутків елементів відповідного рядка матриці А на відповідний стовпчик матриці В. Наприклад, якщо
розмірності т ´ р, кожен елемент якої є сумою добутків елементів відповідного рядка матриці А на відповідний стовпчик матриці В. Наприклад, якщо 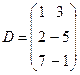 , а
, а 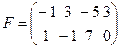 , то
, то  .
.
Зауважимо, що добуток матриць є некомутативною операцією. Так в останньому прикладі добуток FD не існує, оскільки кількість стовпчиків матриці F не дорівнює кількості рядків матриці D. Але навіть якщо обидва добутки
існують, вони, як правило, не рівні між собою. Наприклад,  , але
, але  .
.
Справджуються такі властивості:
1)  2)
2)  3)
3)  7)
7)  8)
8)  9)
9) 
| 4)  5)
5)  6)
6)  10)
10) 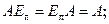 11)
11)  12)
12) 
|
Матриця 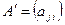 називається транспонованою до матриці
називається транспонованою до матриці 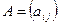 . Очевидно, що коли розмірність матриці А дорівнює т ´ п, то розмірність транспонованої матриці — п ´ т. Наприклад, якщо
. Очевидно, що коли розмірність матриці А дорівнює т ´ п, то розмірність транспонованої матриці — п ´ т. Наприклад, якщо  , то
, то  .
.
Справджуються такі властивості операції транспонування:
1) 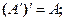 2)
2) 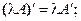
| 3)  4)
4) 
|
|
|
|
|
|
Дата добавления: 2015-05-23; Просмотров: 933; Нарушение авторских прав?; Мы поможем в написании вашей работы!