Системи лінійних алгебричних рівнянь

Система рівнянь виду 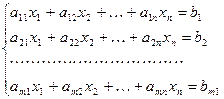називається системою лінійних алгебричних рівнянь.

Якщо ввести позначення , , 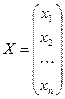, то систему лінійних алгебричних рівнянь можна записати у вигляді: .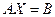

Матрицю 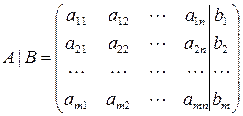називають розширеною ма­три­цею системи. Система лінійних алгебричних рівнянь сумісна (має розв’язки) тоді і лише тоді, коли ранг матриці А системи дорівнює рангу її розширеної матриці. Якщо при цьому кількість невідомих дорівнює цьому рангу, то система має єдиний розв’язок. Якщо кількість невідомих більша, ніж цей ранг, то система має безліч розв’язків.

Якщо матриця А системи лінійних алгебричних рівнянь квадратна і невироджена, то розв’язок системи обчислюємо за формулою 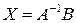. Знаходження розв’язку будь-якої сумісної системи може бути зведене до розв’я­зу­ван­ня системи лінійних алгебричних рівнянь з квадратною матрицею розмірності 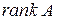відкиданням залежних рівнянь та перенесенням частини невідомих у праву частину системи.

Ненульовий розв’язок Х системи лінійних алгебричних рівнянь 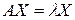з квадратною матрицею А називають власним вектором матриці А, який відповідає власному значенню 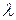цієї матриці. Очевидно, що власні значення матриці А є коренями характеристичного рівняння

.

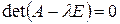Наприклад, власними значеннями матриці 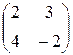є розв’язки рівняння 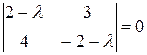(або 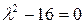), а саме числа 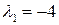і 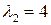. Відповідні їм власні ветори знаходимо як розвязки системи . Зокрема, будь-який вектор 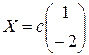, де с — довільна ненульова константа буде власним вектором, що відповідає власному значенню 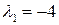, а вектор 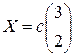— власним вектором, що відповідає власному значенню .

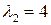Якщо квадратну матрицю А розмірності п розглядати як деякий оператор, який кожний вектор 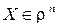переводить у вектор 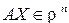, то власні вектори матриці А можна розглядати як інваріантні (незмінні) відносно дії оператора напрямки у просторі .

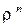Дата добавления: 2015-05-23