П.1. Джерела та класифікація похибок

Метод Ейлера та його модифікації розв’язку задачі коші для звичайних диф. р-нь. Геометричні ілюстрації цих методів.

Нехай дано 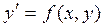, 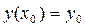а ф-я f(x,y) визначена на [a;b]. Поділимо цей відрізок на n-частин

;

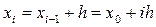Мал. 9.1

Розглянемо відрізок 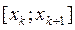про інтегруємо д. р. на цьому вілрізку

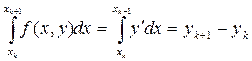
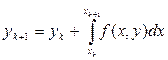
Якщо h мале то ф-ю f(x;y) можна вважати сталою і вона приймає значення лівого кінця відрізка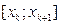

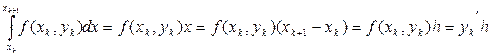
Отже знаходження наближеного розв’язку д.р. за схемою Ейлера відбув. за формулами

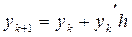
Обчислення y(x) за методом Ейлера зручно записувати у таблиці

i	xi	yi	yi^′=f(xi,yi)	h yi^′
(1)	(2)	(3)	(4)	(5)

1. Заповнимо перший рядок стовпців (1) (2) (3).

2. Обчислимо y_i^′ і записуємо в стовпчик (4)

3. Обчислимо h y_i^′ і записуємо в (5)

4. У стовпчик (3) другого рядка запишемо суму числа з стовпчика (3) і числа (5)

Модифікації:

1). Удосконалений метод Ейлера.

Реалізовують в два етапи.

Обчислюють координати середньої точки проміжка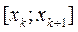

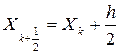
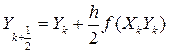
Потім шукають

x=x+h

Y=Y+hf(x,Y)

X=x₀ Y=y₀

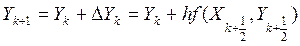
Алгоритм методу Ейлера

- +

В практиці обчислень під наближеним числом а розуміють число, що незначно відрізняється від точного числа А і замінює його в обчисленнях.

Розв’язок більшості практичних задач умовно проводиться в два етапи:

1) математичне описання досліджуваної проблеми

2) розв’язок сформульованої мат. задачі

На 1-му етапі зустрічаються 2 характерних джерела похибок:

1) процеси, що реально протікають не завжди можна описати математично, а введені спрощення дають можливість отримати лише більш-менш ідеалізовані моделі;

2) неточність задання початкових параметрів, які отримують, як правило, із експерименту, який завжди дає лиш наближений результат.

У відповідності до цього сумарна похибка математичної моделі та початкових даних об’єднується в похибку вхідної інформації. ЇЇ часто називають неусуненою похибкою.

На 2-му етапі отримати точний розв’язок математичної задачі не можливо, незалежно від того чи він знаходиться аналітично чи на ЕОМ.

В практичних розрахунках використовуються методи наближеного розв’язку, і в першу чергу, числові. Така вимушена заміна точного розв’язку на наближений породжує похибку методу або похибку апроксимації.

Нарешті, в процесі розв’язку задачі відбувається заокруглення вхідних даних, проміжних та кінцевих результатів. Ці похибки, то похибки, що виникають при виконанні арифметичних операцій з наближеними числами переносяться на результат обчислень і утворюють так звану обчислювальну похибку або похибку заокруглень, або інструментальну.

Виходячи із цього при постановці задачі або вказують необхідну точність розв’язку, тобто задають максимально допустиму похибку в процесі всіх обчислень, або обмежуються вимогами підрахунку сумарної похибки результату. Тому при роботі з наближеними числами необхідно уміти розв’язувати такі задачі:

1) давати мат. характеристики точності наближених чисел;

2) знаючи точність вхідних даних оцінювати точність результату;

3) вибрати вхідні дані з такою точністю, щоб забезпечити задану точність результату;

4) оптимальним чином будувати обчислювальний процес, щоб не проводити розрахунків, які впливають на точні цифри результату.

Дата добавления: 2015-05-23