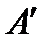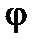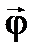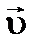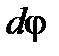Вектор кутового зміщення. Кутові швидкість і прискорення. Зв’язок між кутовими й лінійними величинами

1. Не завжди тіло, рух якого ми вивчаємо, можна вважати матеріальною точкою. Розглянемо наступну модель тіла – абсолютно тверде тіло.

Абсолютно твердим тілом називають тіло, в якому у даних умовах задачі можна знехтувати деформаціями (відстані між довільними двома точками можна вважати постійними).

Рух твердого тіла можна подати як сукупність двох видів руху поступального та обертального.

Поступальним називають такий рух, коли будь-яка пряма, що жорстко пов’язана з тілом, яке рухається, залишається паралельною сама собі. Математично поступальний рух є еквівалентним паралельному перенесенню.

Обертальним називають такий рух, коли усі точки тіла рухаються по колам, центри яких лежать на одній і тій же прямій. Цю пряму називають віссю обертання.

2. Розглянемо детально обертальний рух твердого тіла. Описувати цей рух за допомогою лінійних швидкостей і лінійних прискорень стає незручно, тому що різні точки твердого тіла мають різні швидкості та прискорення. Потрібно ввести величини, які характеризують обертання твердого тіло як цілого.

Виберемо довільну точку твердого тіла (рис.3). Проведемо радіус від центра кола , відносно якого обертається точка до самої точки . Через проміжок часу т. переміститься в положення . Кут характеризує поворот твердого тіла. При цьому довільна пряма, яка проведена в площині, що перпендикулярна до осі обертання (рис. 3), повернеться на такий самий кут 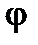(рис. 3). Кут називають кутом повороту.

A

O

Рисунок 3

Для того щоб вказати, в якому напрямку відбувається обертання вводять вектор кутового зміщення. Вектором кутового зміщення 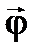називають вектор, модуль якого дорівнює куту повороту, а напрямок пов’язаний з обертанням тіла правилом правого гвинта (див. рис. 4). Встановимо правий гвинт уздовж осі обертання, повернемо його за напрямком обертання твердого тіла, поступальний рух гвинта вкаже на напрямок вектора 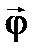. Вектор повороту в системі СІ вимірюється в радіанах.

Для того щоб характеризувати як швидко змінюється вектор повороту 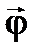, використовують поняття кутової швидкості. Кутовою швидкістю 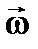називають . Вектор кутової швидкості в системі СІ вимірюється в рад/с.

Вісь обертання

Рисунок 4

Для того щоб характеризувати як швидко змінюється кутова швидкість , використовують поняття кутового прискорення. Кутовим прискоренням 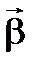називають . Вектор кутового прискорення в системі СІ вимірюється в рад/с².

3. За відомими кутовою швидкістю та кутовим прискоренням можна знайти лінійні швидкості та лінійні прискорення для будь-якої точки твердого тіла.

Розглянемо точку твердого тіла, яка рухається по колу відносно центра кола , який знаходиться на осі обертання (див. рис. 5). За час точка пройде по колу шлях , який відповідає куту повороту 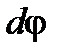. Виходячи з цього, можемо записати

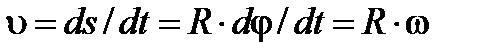. (10)

Для того щоб вказати напрямок вектора, використаємо векторний добуток. Виходячи з напрямків векторів, які зображені на рисунку, можемо записати

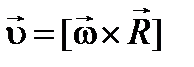. (11)

Цей вираз можна узагальнити. Неважко впевнитися, що коли визначати положення точки відносно довільної розміщеної на осі обертання точки 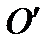вектором 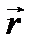(див. рис. 5), то можемо записати

.

. Таким чином, можемо записати

. (12)

Z

O

A

Рисунок 5

Для нормального прискорення можемо записати 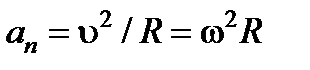. Звідси, з урахуванням напрямків векторів маємо

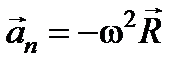. (13)

Для тангенціального прискорення можемо записати

.

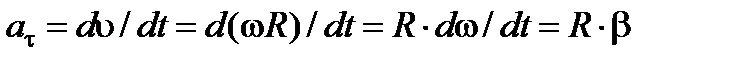Звідси, з урахуванням напрямків векторів запишемо

. (14)

4. Виходячи з інформації про вектор кутового прискорення, можна знайти вектор кутової швидкості, а потім і вектор кутового зміщення.

5. Знайдемо кут повороту та його швидкість, коли тіло має постійне за напрямком і модулем кутове прискорення

Використовуючи, що 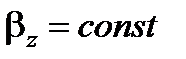, а також вибираючи початковий час таким, що дорівнює нулю , можемо отримати

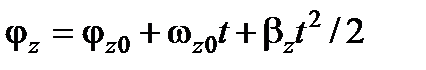, . (15)

Слід також зазначити, що матеріальну точку можна розглядати як частинний випадок абсолютно твердого тіла. Тому отримані результати для абсолютно твердого тіла, можна застосувати і для матеріальної точки, яка рухається по колу.

Дата добавления: 2015-05-23