
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тестові завдання. 1 Який з наведених виразів є математичним записом визначення кутового прискорення тіла?
|
|
|
|
1 Який з наведених виразів є математичним записом визначення кутового прискорення тіла?
А) 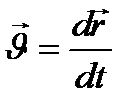 ; Б)
; Б) 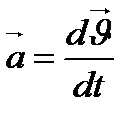 ; В)
; В) 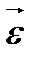 =
= 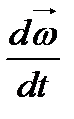 ; Г)
; Г) 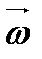 =
= 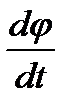
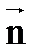 .
.
2 Яка з умов визначає рівномірний рух по колу?
А) а t = const; а n = 0; Б) а t ≠ const; а n = const;
В) а t = 0; а n = 0; Г) а t = 0; а n = const
3 Яке твердження є продовженням виразу: сила – це
А) єдина міра різних форм руху;
Б) міра взаємодії тіл або частин тіла;
В) міра гравітаційних та інертних властивостей тіла;
Г) міра інертності тіла в обертальному русі.
4 Який з наведених виразів є математичним записом визначення моменту інерції матеріальної точки?
А) 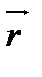
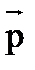 ; Б)
; Б) 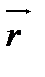
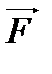 ; В) mr2; Г) Smiri2.
; В) mr2; Г) Smiri2.
5 Чому дорівнює момент інерції стрижня відносно осі, проведеної через його середину?
А) 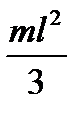 ; Б)
; Б) 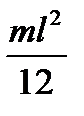 ; В)
; В) 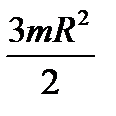 ; Г) 2 mR2.
; Г) 2 mR2.
6 Матеріальна точка переміщується по колу радіусом 20 см рівноприскорено з тангенціальним прискоренням 5 м/с2. Через який час після початку руху її нормальне прискорення буде у 2 рази більше, ніж тангенціальне?
А) 3,25 с; Б) 2,54 с; В) 2,78 с; Г) 3,4 с.
7 Диск радіусом 20 см починає обертатися з кутовим прискоренням 3 с-2. Через який час точка, що лежить на його краю, буде мати прискорення 75 см/с2?
А) 0,5 с; Б) 1,5 с; В) 2,5 с; Г) 3 с.
8 Колесо, яке обертається рівноприскорено, досягло кутової швидкості w =20 с-1 через N = 10 об після початку обертання. Знайти кутове прискорення колеса.
А) 2,25 с-2; Б) 3,2 с-2; В) 1,2 с-2; Г) 2,8 с-2.
9 Махове колесо радіусом 1 м починає рух із стану спокою та обертається рівноприскорено. Через 10 с точка, що лежить на його ободі, набуває швидкості 100 м/с. Знайти швидкість, а також нормальне, тангенціальне і повне прискорення цієї точки в момент часу 15 с.
А) 150 м/с; 10 м/с2; 2,25105 м/с2; 2,25104 м/с2; Б) 50 м/с; 10 м/с2; 1,25105 м/с2; 3,25104 м/с2;
В) 180 м/с; 12 м/с2; 3,02105 м/с2; 2,25104 м/с2; Г) 150 м/с; 9 м/с2; 1,25103 м/с2; 2,25104 м/с2.
10 Махове колесо, яке оберталося зі швидкістю 4 об/с, зупиняється протягом 30 с. Вважаючи його рух рівномірно сповільненим, знайти, скільки обертів воно зробило до зупинення.
А) 40 обертів; Б) 50 обертів; В) 60 обертів; Г) 70 обертів.
11 Колесо, яке обертається рівносповільнено, при гальмуванні зменшило власну частоту обертання за 1 хв. з 5 об/с до 3 об/с. Знайти кутове прискорення та кількість обертів, яке зробило колесо за цей час.
А) - 0,46 с-2, 140 об; Б) - 0,59 с-2, 260 об;
В) - 1,21 с-2, 340 об; Г) - 0,21 с-2, 240 об.
12 Знайти радіус колеса, що обертається, якщо відомо, що лінійна швидкість точки, яка лежить на ободі, в 2,5 раза більша від лінійної швидкості точки, що лежить на 5 см ближче до осі колеса.
А) 6,33 см; Б) 7,33 см; В) 8,33 см; Г) 9,33 см.
13 Махове колесо через 1 хв. після початку руху набуває швидкості, що відповідає 12 об/с. Знайти кутове прискорення колеса і число обертів колеса за цю хвилину. Рух вважати рівноприскореним.
А) 1,26 с-2; 360 об; Б) 2,34 с-2; 380 об; В) 0,26 с-2; 140 об; Г) 1,26 с-2; 260 об.
14 Точка рухається по колу радіусом 10 см зі сталим тангенціальним прискоренням. Знайти тангенціальне прискорення точки, якщо відомо, що у кінці п’ятого оберту від початку руху швидкість точки стала 79,2 см/с.
А) 0,1 м/с2; Б) 0,3 м/с2; В) 0,4 м/с2; Г) 0,2 м/с2.
15 Маховик, одержав початкову кутову швидкість 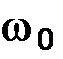 = 2с-1. Зробивши 10 оборотів, він, унаслідок тертя в підшипниках, зупинився. Знайти кутове прискорення маховика, вважаючи його сталим.
= 2с-1. Зробивши 10 оборотів, він, унаслідок тертя в підшипниках, зупинився. Знайти кутове прискорення маховика, вважаючи його сталим.
А) -0,1 с -2; Б) -0,2 с -2; В) -0,4 с -2; Г) -0,6 с -2.
16 Точка рухається по колу радіусом 20 см зі сталим тангенціальним прискоренням 5 см/с2. Через який час від початку руху нормальне прискорення точки буде втричі більше від тангенціального?
А) 3,46 с; Б) 2,51 с; В) 4,09 с; Г) 3,16 с.
17 Поїзд рухається по заокругленню радіусом 400 м, причому його тангенціальне прискорення дорівнює 0,2 м/с2. Визначити його нормальне і повне прискорення в той момент, коли його швидкість дорівнює 10 м/с.
А) 2,25 м/с2; 3,32 м/с2; Б) 1,25 м/с2; 1,32 м/с2;
В) 0,25 м/с2; 0,32 м/с2; Г) 0,45 м/с2; 2,72 м/с2.
18 Поїзд в’їжджає на заокруглену ділянку з початковою швидкістю 10 м/с і проходить шлях 600 м за 30 с. Радіус заокруглення дорівнює 1 км. Визначити швидкість і повне прискорення поїзда в кінці повороту.
А) 30 м/с; 1,12 м/с2; Б) 20 м/с; 3,12 м/с2;
В) 10 м/с; 0,64 м/с2; Г) 40 м/с; 2,12 м/с2.
19 Камінь, прив’язаний до мотузки, рівномірно обертається у вертикальній площині. Знайти масу каменя, якщо відомо, що різниця між максимальною і мінімальною силами натягу мотузки 10 Н.
А) 0,25 кг; Б) 0,5 кг; В) 0,75 кг; Г) 1,0 кг.
20 На барабан радіусом 0,5 м намотано шнур, до кінця якого прив’язаний вантаж масою 10 кг. Знайти момент інерції барабана, якщо відомо, що вантаж опускається з прискоренням 2,04 м/с2.
А) 7,5 кг м2; Б) 8,5 кг м2; В) 9,5 кг м2; Г) 1,5 кг м2.
21 До обода колеса, яке має форму диска, радіусом 0,5 м та масою 50 кг, прикладена дотична сила 100 Н. Знайти кутове прискорення колеса та через скільки часу після початку дії сили колесо буде мати швидкість, яка відповідає 100 об/с?
А) 5,8 с 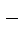 2; 40 c; Б) 7,8 с
2; 40 c; Б) 7,8 с 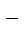 2; 80 c; В) 6,8 с
2; 80 c; В) 6,8 с 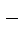 2; 70 c; Г) 9,8 с
2; 70 c; Г) 9,8 с 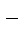 2; 100 c.
2; 100 c.
22 Диск масою 2 кг і радіусом 10 см обертається навколо горизонтальної осі, що проходить через його центр, із частотою 600 об/ хв. Через 20 секунд під дією гальмівного моменту диск зупиняється. Знайти гальмівний момент.
А) 1,1 10-2 Н м; Б) 3,1 10-2 Н м;
В) 2,5 10-2 Н м; Г) 5,8 10-2 Н м.
23 Суцільна кулька масою 400 г і радіусом 5 см обертається навколо осі, що проходить через її центр. Закон обертання кульки має вигляд = 4 + 2t 2t2. Визначити гальмівний момент.
А) 1,6 10-3Н м; Б) 2,68 10-3Н м;
В) 1,9 10-3Н м; Г) 1,3 10-3Н м.
24 Диск масою 0,5 кг і радіусом 0,06 м обертається навколо горизонтальної осі, що проходить через його центр. Закон обертання має вигляд = 8 2t + 6t2. Визначити момент сили, що діє на диск.
А) 0,011 Н м; Б) 0,022 Н м; В) 0,033 Н м; Г) 0,044 Н м.
25 Диск масою 2 кг і радіусом 0,1 м обертається навколо осі, що проходить через його центр. Рівняння руху = 5 6t2 + t3. Визначити момент сил, що діють на диск, в момент часу 4 с. Визначити закон зміни моменту сил.
А) 0,20 нм; М = 1,12 + 3,06t; Б) 0,12 нм; М = 0,12 + 0,06t;
В) 1,72 нм; М = 0,12 + 0,06t; Г) 3,12 нм; М = 4,15 + 0,86t.
26 На барабан радіусом 0,5 м намотано шнур, до кінця якого прив’язано вантаж масою 2 кг. Знайти момент інерції барабана, якщо відомо, що вантаж опускається з прискоренням 2,04 м/с2.
А) 1,5 кг м2; Б) 1,7 кг м2; В) 1,9 кг м2; Г) 2,3 кг м2.
27 До обода однорідного диска радіусом 0,2 м прикладено дотичну силу 98,1 Н. При обертанні на диск діє момент сил тертя 4,9 Нм. Знайти масу диска, якщо відомо, що він обертається з кутовим прискоренням 100 рад/с2.
А) 4,28 кг; Б) 1,9 кг; В) 7,36 кг; Г) 5,0 кг.
28 Маховик, момент інерції якого 63,6 кгм2, обертається з кутовою швидкістю 31,4 рад/с. Знайти момент сил гальмування, під дією якого маховик зупиняється через 20 с. Маховик вважати однорідним диском.
А) М = 10 Нм; Б) М = 20 Нм; В) М = 30 Нм; Г) М = 40 Нм.
29 Тверде тіло масою 4 кг обертається відносно деякої осі за законом = 5 + 10t + 0,5t2. Момент сил відносно цієї осі дорівнює 2 Н м. Визначити власний момент інерції, якщо відстань між осями 0,5 м.
А) 1 кгм2; Б) 2 кгм2; В) 1,44 кгм2; Г) 2,56 кгм2.
30 Кільце масою 2 кг і радіусом 0,1 м обертається відносно осі, перпендикулярної до площини кільця, яка проходить через кінець радіуса, за законом = 8 2 t2 + 2t3. Визначити обертальний момент сил в момент часу 1 с.
А) 2 Нм; Б) 3 Нм; В) 4 Нм; Г) 5 Нм.
31 Маса кулі 5 кг, радіус 0,2 м. Вісь обертання проходить через середину радіуса і напрямлена перпендикулярно радіусу. Визначити момент інерції й момент імпульсу кулі в момент часу 1 с, якщо вона обертається за законом = 5 + 2t + t2.
А) 0,13 кг м2; 0,52 кг м2/с; Б) 1,23 кг м2; 2,72 кг м2/с;
В) 2,51 кг м2; 0,52 кг м2/с; Г) 0,13 кг м2; 1,49 кг м2/с.
32 Горизонтальна платформа масою 250 кг обертається навколо вертикаль-ної осі, виконуючи 20 об/хв. На краю платформи стоїть людина масою (точковою) 80 кг. З якою частотою буде обертатися платформа, якщо людина переміститься на 0,5 R до центра платформи?
А) 0,25 об/с; Б) 0,47 об/с; В) 0,68 об/с; Г) 0,91 об/с.
33 Куля котиться без ковзання по горизонтальній поверхні. Повна кінетична енергія кулі дорівнює 14 Дж. Визначити кінетичну енергію поступального та обертального руху кулі.
А) 6 Дж, 1 Дж; Б) 7 Дж, 2 Дж;
В) 8 Дж, 4 Дж; Г) 10 Дж, 4 Дж.
34 Хлопчик котить обруч по горизонтальній дорозі зі швидкістю 7,2 км/год. На яку відстань може викотитись обруч на гірку за рахунок його кінетичної енергії? Нахил гірки становить 10 м на кожні 100 м шляху.
А) 3,1 м; Б) 4,1 м; В) 5,1 м; Г) 1,1 м.
35 Маховик і легкий шків насаджені на горизонтальну вісь. До шківа за допомогою нитки прив’язано вантаж, який, рівноприскорено опускаючись, пройшов 2 м за 4 с. Момент інерції маховика 0,05 кгм2. Визначити масу вантажу, якщо радіус шківа 6 см. Масою шківа знехтувати.
А) 0,36 кг; Б) 0,58 кг; В) 0,79 кг; Г) 1,03 кг.
36 Маховик, момент інерції якого 40 кгм 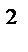 , почав обертатися рівноприскорено із стану спокою під дією моменту сили 20 Нм. Обертання тривало протягом 10 с. Визначити кінетичну енергію, яку набуде маховик.
, почав обертатися рівноприскорено із стану спокою під дією моменту сили 20 Нм. Обертання тривало протягом 10 с. Визначити кінетичну енергію, яку набуде маховик.
А) 200 Дж; Б) 350 Дж; В) 450 Дж; Г) 500 Дж.
ВИКЛАДАЧ – Марінець І.С.
САМОСТІЙНА РОБОТА № 2 (2 год.)
ТЕМА: Основні положення спеціальної теорії відносності (СТВ). Закон взаємозв’язку маси та енергії
МЕТА: поглибити знання про основні поняття спеціальної теорії відносності; пояснити сутність постулатів СТВ; познайомити з історією створення СТВ; пояснити взаємозв’язок маси та енергії; розглянути фізичну суть закону взаємозв’язку маси й енергії; розвивати логічне мислення студентів; виховувати бажання самостійно отримувати знання.
ПЕРЕЛІК ПОСИЛАНЬ:
1 Бар’яхтар В.Г. Фізика. 10 кл. Підручник для загальноосвітніх навчальних закладів / В.Г. Бар’яхтар, Ф.Я. Божинова.-Х.: Видавництво «Ранок», 2010, с. 234-246
2 Бушок Г.Ф.Курс фізики. Кн.1. Фізичні основи механіки. Молекулярна фізика і термодинаміка / Г.Ф. Бушок, Є.Ф. Венгер. – К.: Вища школа, 2002, с. 137-168
3 Кучерук І.М. Загальний курс фізики. У трьох томах. Т. 1. Механіка. Молекулярна фізика і термодинаміка / І.М.Кучерук, І.Т Горбачук, П.П. Луцик. – К.: Техніка, 2006, с. 189-205
|
|
|
|
|
Дата добавления: 2015-05-23; Просмотров: 2018; Нарушение авторских прав?; Мы поможем в написании вашей работы!