Тема 1. Основи хімічної термодинаміки та практичне застосування її положень в хіміко-технологічних розрахунках 2 страница

Прийнято рахувати, що при ⁰ К ентропія речовини дорівнює нулю, оскільки при цій температурі розміщення атомів або молекул в кристалічній структурі характеризується максимальним порядком.

З підвищенням температури ентропія завжди зростає. Вона стрибкоподібно збільшується при послідовному переході речовини з твердого кристалічного стану у газоподібний стан.

На рис.1.6 приведена типова крива зміни ентропії речовини при її нагріванні. Відрізок ОА характеризує поступове збільшення значень ентропії від 0 до температури плавлення (Т_ПЛ). В точці плавлення А відбувається стрибок ентропії (відрізок АВ) на ΔS_ПЛ. Відрізок ВС характеризує збільшення значень ентропії при нагріванні рідкої речовини від температури кипіння (Т_КИП). В точці кипіння С також відбувається стрибок ентропії (відрізок СD) на ΔS_ВИП. Стрибкоподібна зміна ентропії в точках плавлення і кипіння відбувається при постійній температурі. При подальшому нагріванні (крива DE) ентропія газоподібної речовини знов плавно зростає.

Рис.1.6. Залежність ентропії від температури

В разі збільшення тиску в системі або при охолодженні зміна ентропії відбувається в зворотному напрямку, яка характеризується кривими ЕD, СВ і АО. При цьому в точках D (початок конденсації) і В (початок кристалізації) спостерігається стрибкоподібне зменшення значень ентропії при сталих температурах. Зміна значень ентропії в процесах конденсації (ΔS_КОНД) і кристалізації (ΔS_КР) дорівнює значенням ΔS_КИП і ΔS_ПЛ відповідно.

Ентропія як функція системи підкоряється закону Гесса. Це можна довести розглядаючи процеси переходу води із одного стану в інший. Так процес переходу льоду у пару можливий за двома шляхами.

Перший – через плавлення і випаровування рідини. В цьому випадку зміна ентропії складає:

Другий шлях – безпосередній перехід молекул води із льоду в пару – сублімація (возгонка). Зміна ентропії сублімації дорівнює:

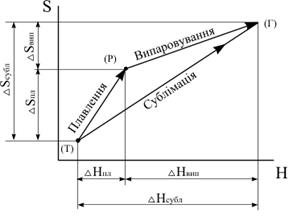
Отже, зміна ентропії, як і зміна ентальпії, не залежить від способу переходу, при умові, що вихідний і кінцевий стани речовини однакові. Це ілюструє рис.1.7 на якому показані зміни ентропії і ентальпії води при фазових переходах.

Рис.1.7. Зміна ентропії і ентальпії при фазових переходах

З наведеного випливає, що зміна ентропії складного процесу, дорівнює сумі змін ентропії кожної окремої стадії цього процесу:

(1.33)

Наприклад, якщо переохолоджений лід при температурі -10⁰ С поступово нагрівати до перетворення його у пару з температурою 120⁰ С загальна зміна ентропії буде дорівнювати сумі змін ентропії таких стадій:

1) нагрівання льоду від –10 до 0⁰ С, ΔS₁;

2) плавлення льоду, ΔS_ПЛ;

3) нагрівання води від 0 до температури кипіння 100⁰ С, ΔS₂;

4) випаровування води, ΔS_ВИП;

5) нагрівання пари від 100 до 120⁰ С, ΔS₃.

За другим законом термодинаміки при нагріванні системи (абсолютна ентропія) чисельно дорівнює:

(1.34)

де С - молярна теплоємність речовини.

Використовуючи значення стандартної ентропії визначають абсолютну ентропію при будь-якій температурі за рівнянням:

(1.35)

Загальний вираз для розрахунку температурної залежності ентропії речовини, що знаходиться в стандартному стані і характеризується фазовими переходами, має вигляд:

(1.36)

Для хімічної реакції, що відбувається при температурі Т, зміна ентропії хімічного процесу дорівнює різниці абсолютних ентропій продуктів реакції і вихідних речовин:

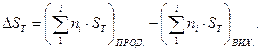(1.37)

Енергія Гібсса. Напрямок хімічної реакції. Узагальнені рівняння першого і другого законів термодинаміки (співвідношення Максвела) відображають зв'язок між ентропією і параметрами стану системи (тиск, температура, об'єм). Характеристичними функціями, виведеними на підставі співвідношень Максвела, є енергія Гіббса (ізобарно-ізотермічний потенціал):

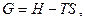(1.38)

і енергія Гельмгольца (ізохорно-ізотермічний потенціал):

(1.39)

Ізобарний і ізохорний потенціали є функціями стану системи і їх використовують для визначення напрямку процесу в умовах термодинамічної рівноваги.

Перебіг самочинного процесу в неізольованій системі можливий лише в напрямку, при якому за умов Т=const, Р=const зменшується енергія Гіббса і за умов Т=const, V=const зменшується енергія Гельмгольца, тобто ΔG < 0 і ΔF < 0.

Якщо ΔG > 0 і ΔF > 0 зміна стану системи відбувається тільки при використанні зовнішньої роботи. У випадку коли ΔG і ΔF дорівнюють нулю, то система перебуває у рівновазі.

Зміну енергії Гіббса в хімічній реакції розраховують за рівнянням Гіббса – Гельмгольца:

(1.40)

В цьому рівнянні

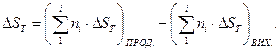
В температурному інтервалі 298 – Т враховується температурна залежність ΔG˚_Т = f(Т) у вигляді рівності:

(1.41)

Рівняння (1.41) вирішується методом розкриття інтегралів:

Можливе виключення інтегральних величин Δс’/Т або Δb·Т+ Δс’/Т², що спрощує розрахунок, але при цьому точність розрахунку зменшується.

З рівняння Гіббса-Гельмгольца випливає:

1) якщо ΔН < 0 і ΔS > 0 то завжди ΔG < 0, тобто реакція з виділенням теплоти і збільшенням степені невпорядкованості можлива при всіх температурах;

2) якщо ΔH > 0 і ΔS < 0, то завжди ΔG > 0, тобто реакція з поглинанням теплоти і збільшенням степені упорядкованості неможлива ні при яких умовах;

3) у рештах випадках (ΔН < 0, ΔS < 0 і ΔН >0, ΔS > 0) знак ΔG залежить від співвідношення членів ΔН і ТΔS. Реакція можлива, тільки якщо вона супроводжується зменшенням ізобарного потенціалу;

4) при кімнатній температурі, коли значення Т невелике, значення добутку ТΔS також невелике (рис.1.8), і звичайно зміна ентальпії переважує ТΔS. Тому більшість реакцій, які відбуваються при кімнатній температурі, - це реакції з виділенням теплоти (ΔН < 0). При збільшенні температури збільшується і добуток ТΔS, тому при високих температурах навіть реакції з поглинанням теплоти (ΔН > 0) стають самовільними.

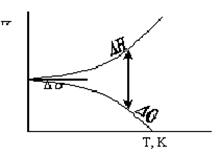
Рис.1.8. Залежність ∆Н і ∆G від температури

Слід відмітити, що хімічні реакції, під час перебігу яких відбувається зменшення термодинамічних потенціалів, називають екзергонічними, а якщо потенціали зростають – ендергонічними. При ізохорному процесі самовільна реакція можлива тільки при ΔF < 0. Для ΔF тлумачення точно такі, як і для ΔG. Чисельно ΔG і ΔF відрізняються на роботу розширення.

Зв'язок між основними термодинамічними функціями ілюструє діаграма, що зображена на рисунку:

Рис. 1.9. Діаграма співвідношень основних термодинамічних функцій

З аналізу співвідношень витікає, що:

при Т→ 0 і Р → 0 ∆G → ∆F, а при Т = 0, Р = 0 і ∆n = 0 ∆G = ∆F.

Крім того, чим більше ∆n і тиск в реакційній системі, тим більше чисельне значення роботи розширення.

В табл. 1.1. співставлені форми характеристичних функцій, їх зміна при одному постійному параметрі стану і сумарні інтегральні форми.

Таблиця 1.1

Характеристичні функції і їх перемінні

Характеристичні функці	Параметри стану	Диференційна функція	Прийнята інтегральна форма
Внутрішня енергія U (ізохорно-ізоентропійний потенціал)	S, V	dV-TdS-PdV	При S=const ΔUS = -RTln(V2/V1) При V=const ΔUV=T(S2-S1) U=F+TS
Ентальпія Н (ізобарно-ізоентропійний потенціал)	S, P	dH-TΔS+VdP	При S=const ΔНS = RTln(Р2/Р1) При Р=const ΔНР=T(S2-S1) Н=U+pV

продовження табл. 1.1

Енергія Гельмгольца F (ізохорно-ізотермічний потенціал)	V, T	dF=-PdV-SdT	При V=const ΔFV = Qутв.ln(T1/T2) При T=const FT=ΔUT F=U-TS
Енергія Гіббса (ізобарно-ізотермічний потенціал)	P, T	dG=VdP-SdT	При P=const ΔGP = Qутв.ln(T1/T2) При T=const GT= RTln(Р2/Р1) G=F+pV

Теплота фазових перетворень. Залежність теплоти фазового перетворення від умов його проходження для будь-якого рівноважного процесу визначається за рівнянням Клаузіуса – Клапейрона:

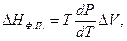(1.42)

де Н_Ф.П. – теплота фазового перетворення (плавлення, випаровування, поліморфного перетворення, сублімації тощо); ∆V – зміна об'єму при фазовому переході, dp/dT – похідна, що зв'язує зміну температури і тиску за умови збереження стану рівноваги між фазами.

Теплота плавлення – переходу твердої фази в рідку - завжди позитивна. Об'єм рідкої фази (V_Р) в загальному випадку може бути більше або менше об'єму в тій же кількості твердої фази (V_Т). Звідси витікає, що величина dp/dТ, яка характеризує зміну температури від тиску, може бути позитивною або від'ємною тобто, температура плавлення може підвищуватись або знижуватись зі збільшенням тиску.

Величина dТ/dР має від'ємне значення лише для води і деяких інших речовин, у яких густина рідини при температурі плавлення більше густини твердої фази.

Рівняння Клаузіуса-Клапейрона в цьому випадку набуває вигляду:

(1.43)

При випаровуванні – переходу рідкої фази в газоподібну – теплота випаровування також позитивна, а температура випаровування завжди підвищується зі зростанням тиску.

В зв'язку з тим, що мольний об'єм пари значно перевищує мольний об'єм рідини значення V_р в рівнянні можна знехтувати і воно прийме вигляд:

(1.44)

Якщо насичену пару рахувати ідеальним газом, тобто

Тоді рівняння (1.44) набуде вигляду:

(1.45)

В області невисоких тисків теплоти випаровування порівняно мало змінюється з температурою, тому її можна вважати сталою. В цьому випадку після перетворення цього рівняння дістанемо рівняння:

або

(1.46)

які широко застосовуються в практиці.

Практичне застосування термодинамічних розрахунків. Розглянемо розрахунок основних термодинамічних величин на прикладі хімічної реакції, яка відбувається в гомогенній системі:

Н2(Т)+СО2(Г)=Н2О(Г)+СО(Г);

∆НТ=?

при температурі 2000 К і тиску 3 атмосфери.

З довідника виписуємо термодинамічні величини для вихідних сполук і продуктів реакції.

Речовина	∆Н^0298, кДж/моль	S^0298, Дж/(мольК)	Теплоємність, Дж/(моль К)	Темпера-турний інтервал, К
Коефіцієнти рівняння Ср=f(T)
a	b	c
Н2(г)		130,6	27,28	3,26	0,50	298 – 3000
СО2(г)	- 393,5	213,6	44,14	9,04	- 8,53	298 – 2500
Н2О(г)	- 241,8	188,7	30,00	10,71	0,33	298 – 2500
СО(г)	- 110,5	197,4	20,41	4,10	- 0,46	298 – 5000

За рівнянням Гесса визначаємо зміну стандартної ентальпії:

оскільки реакція ендотермічна.

Стандартну зміну ентропії визначаємо за рівнянням:

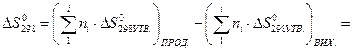
Зміну стандартного потенціалу (енергія Гіббса) визначаємо за рівнянням Гіббса-Гельмгольца за першого припущення (∆С_р = 0):

Оскільки реакція необоротна.

Залежність теплоємності всіх речовин (газів), що приймають участь в реакції, від температури визначаємо за температурним рядом:

Тоді зміна теплоємності для хімічної реакції буде:

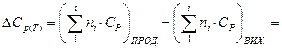
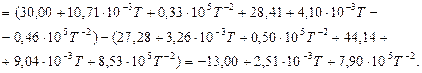
За стандартних умов:

При другому наближенні (С_Р=const) приймаємо:

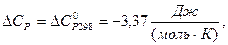
тоді залежність ентальпії від температури (1.28) буде мати вигляд:

Значення ентальпії при температурі реакції складе:

Аналогічно знаходимо ентропію реакції, користуючись рівнянням:

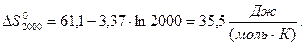
Більш точний розрахунок значень ентальпії і ентропії проведемо, застосовуючи температурну залежність теплоємності хімічної реакції:

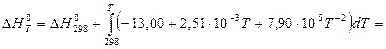
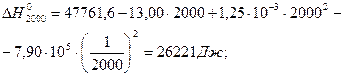
За ентропійною формулою, за умови ∆С_р = const, значення енергії Гіббса при температурі реакції дорівнює:

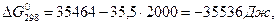
а враховуючи температурну залежність ∆С_р = f (T) складає:

В першому наближенні (С_р = 0, ∆Н⁰_Т = ∆Н⁰₂₉₈ = 41200 Дж) за рівнянням Гіббса-Гельмгольца (у формі невизначеного інтеграла):

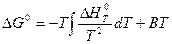
знаходимо значення постійної інтегрування В для Т = 298 К:

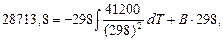
Тоді:

В другому наближенні (∆С_р = const = ∆С⁰_{р 298}):

Звідки постійна інтегрування В при Т = 298 К дорівнює:

Тоді,

При більш точному розрахунку значення ∆G⁰_T:

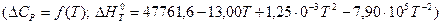маємо:

або

.

звідки В = -137,2.

Тоді:

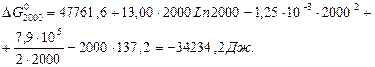
Розглянемо термодинамічний розрахунок для хімічної реакції, що відбувається в гетерогенній системі при температурі 500–700 К.

Вихідні дані для реакції:

Речовина	∆Н^0298 , кДж/моль · К	S^0298, кДж/мол·ьК	Теплоємність, Дж/(мольК)	Темпера-турний інтер- вал, К
Коефіцієнти рівняння Ср = f(T)
a	b	c
MnO2(K)	-519,65	53,14	69,45	10,21	-16,23	273 –773
HCl(Г)	-92,30	186,70	26,53	4,60	1,09	298 –2000
MnCl2(K)	-468,61	117,15	75,48	13,22	-5,73	273 –923
H2O(Г)	-241,84	188,74	30,00	10,71	0,33	298–2500
Cl2(Г)		223,0	36,69	1,05	-2,52	273-1500

Визначаємо зміну стандартних ∆Н⁰₂₉₈ і ∆S⁰₂₉₈:

(реакція екзотермічна).

.

Зміну енергії Гіббса ∆G⁰₂₉₈ визначаємо за ентропійним рівнянням при першому припущенні (∆С_р = 0):

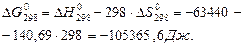
Оскільки реакція при температурі 298 К відбувається самовільно.

Зміну теплоємності для хімічної реакції знаходимо за температурними рядами:

Приймаючи ∆С_р=∆С⁰_р298 знаходимо зміну ентальпії та ентропії системи:

При більш точному розрахунку (∆С _р= f(Т)) ці рівняння мають вигляд:

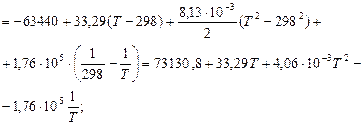
За наближеними і більш точними рівняннями розраховуємо значення ∆Н⁰_Т та ∆S⁰_Т при температурах реакції 500 і 700 К:

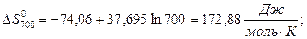
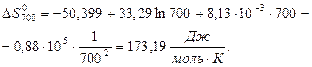
Розрахунок ∆G⁰_T проводимо за ентропійними формулами при припущенні, що ∆С_р = const:

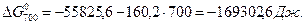
При припущені, що ∆С_р = f (T) ∆G⁰_T дорівнює:

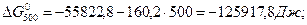
За рівнянням Гіббса-Гельмгольца при першому наближенні (∆С_р = 0, 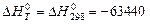Дж), використовуючи значення Дж при температурі 298 К знаходимо постійну інтегрування В:

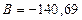
Тоді:

При другому наближенні (∆С_р = const = ∆C_p298):

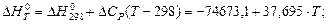
Для Т = 298 К:

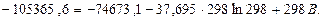
Звідки В = 111,7

Тоді: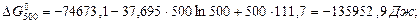

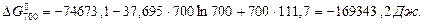
При більш точному розрахунку (С_р = f (T)):

Для Т = 298 К:

Звідки В = 82,69.

Тоді:

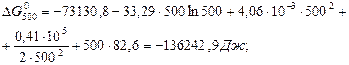
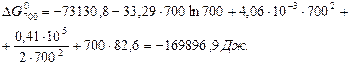
Оцінка похибки при розрахунках 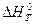, і виконується в порівнянні з найбільш точним результатом. Для ∆ при температурі 500 К різниця між точним і наближеним значенням складає:

55825,6 – 85822,8=2,8 (Дж), або

відносна похибка:

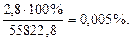
Для :

і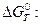

Запитання для самоконтролю

1. Навести методи розрахунків теплових ефектів реакцій.

2. Сформулювати закон Гесса та його наслідки.

3. Виведіть усі можливі співвідношення між термодинамічними функціями H, U, G, F, S.

4. У чому полягає зміст другого закону термодинаміки?

5. Що характеризують термодинамічні потенціали? Для вирішення яких питань вони використовуються?

6. Які величини входять до рівняння ізотерми хімічної реакції?

Дата добавления: 2015-05-23