
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тема 3. Хімічна кінетика 2 страница
|
|
|
|
Здійснюючи поділ змінних і, інтегруючи від 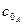 до
до  та від 0 до
та від 0 до 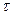 дістанемо:
дістанемо:
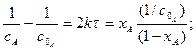 (3.36)
(3.36)
звідки:
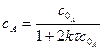
| і |  (3.37) (3.37)
|
Розмірність 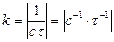 , тобто числове значення k залежить від способу вираження концентрації:
, тобто числове значення k залежить від способу вираження концентрації: 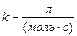 .
.
Відповідно з рівняння 3.36:
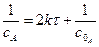
лінійна залежність в координатах 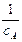 від
від 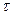 свідчить про те, що реакція, яка розглядається, має другий порядок (рис.3.9), а тангенс кута нахилу
свідчить про те, що реакція, яка розглядається, має другий порядок (рис.3.9), а тангенс кута нахилу  прямої дорівнює числовому значенню константи швидкості k.
прямої дорівнює числовому значенню константи швидкості k.
Період напівперетворення речовини А обернено пропорційний початковій концентрації реагуючих речовин:
 (3.38)
(3.38)
На рисунку 3.9 періоди напівперетворень зображені точками перетину прямої залежності з абсцисою.
Щоб визначити кількість речовини х, яка прореагувала за проміжок часу 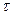 , враховуючи, що
, враховуючи, що
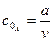 і
і 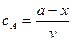
з рівняння 3.37 одержимо:
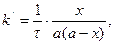 (3.39)
(3.39)
де -  - замість 2k; а – маса реагуючої речовини в початковій момент.
- замість 2k; а – маса реагуючої речовини в початковій момент.
|
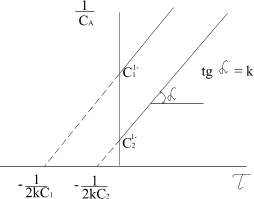
Рис.3.9. Залежність 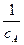 від від 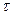 для необоротної
реакції другого порядку (2А=В+D) для необоротної
реакції другого порядку (2А=В+D)
|
Звідси:
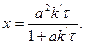 (3.40)
(3.40)
Якщо в реакції кількість реагуючих речовин неоднакова константу швидкості реакції другого порядку знаходять інтегруючи такий вираз:
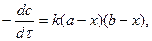
де а і b – початкові концентрації першої і другої речовини, х – концентрації першої і другої речовини, які прореагували за час 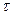 .
.
Інтегрування цього рівняння дає вираз:

| або | 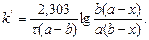
| (3.41) |
Для оборотної бімолекулярної реакції другого порядку типу:
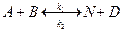
рівняння її швидкості має вигляд:
 . (3.42)
. (3.42)
Значення швидкості оборотної реакції залежить від співвідношення реагентів.
У випадку коли:
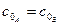
швидкість утворення продуктів реакції виражається рівнянням:
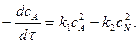 (3.43)
(3.43)
При досягненні рівноваги, враховуючи, що
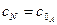
маємо:
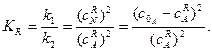 (3.44)
(3.44)
Перетворюючі два останні рівняння одержуємо:

Проінтегрувавши це рівняння швидкості, дістанемо:
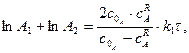 (3.45)
(3.45)
| де | 
| 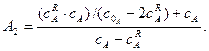
|
Графічна залежність виразу А2 від часу 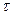 (рис. 3.10) є прямою лінією з кутовим коефіцієнтом, що дорівнює множнику біля
(рис. 3.10) є прямою лінією з кутовим коефіцієнтом, що дорівнює множнику біля 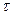 в рівнянні. Пряма відсікає від ординати відрізок, що дорівнює значенню виразу
в рівнянні. Пряма відсікає від ординати відрізок, що дорівнює значенню виразу 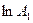 в рівнянні.
в рівнянні.
Константи швидкостей оборотної реакції цього типу можна оцінити, як і оборотну реакцію першого порядку за кутовим коефіцієнтом дотичної на початковій ділянці кривої  (див.вище).
(див.вище).
З виразу початкової швидкості оборотної реакції другого порядку:
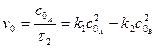
|
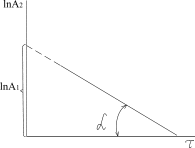
Рис.3.10. Залежність 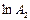 від часу для оборотної реакції
другого порядку (типу від часу для оборотної реакції
другого порядку (типу 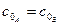 ) )
|
при  дістанемо
дістанемо 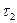 :
:
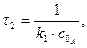
а 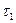 з виразу:
з виразу:
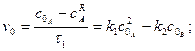

При

інтегрування загального рівняння швидкості оборотної реакції другого порядку дає:
 (3.46)
(3.46)
де 
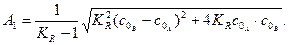
Реакції третього і n -го порядків. Швидкість необоротної хімічної реакції третього порядку, коли речовини А, В і D взяті в нееквівалентних кількостях (кількість молів a, b і d неоднакова) описується рівнянням:
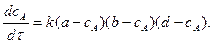
Інтегрування цього рівняння дозволяє отримати вираз для розрахунку часу реакції за умов:

| при | 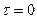 : :
|
 (3.47)
(3.47)
Якщо речовини В і D мають неоднакову кількість (b) молей, то швидкість описується рівнянням:

Відповідно час хімічної взаємодії можна розрахувати за формулою:
 (3.48)
(3.48)
На практиці порядки реакцій визначають користуючись методом Вант-Гоффа за рівняннями:
 і
і 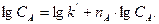
Кінетичний порядок може приймати також дробні і навіть від’ємні значення. Так, швидкість термічного розкладання ацетатного альдегіду в газовій фазі пропорційна його концентрації в ступені  :
:
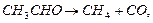
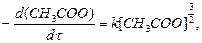
звідки  .
.
В таблиці „Кінетичні закономірності для реакцій з різними кінетичними порядками” приведені кінетичні закономірності для реакцій з різними кінетичними порядками (див. додаток).
Складні реакції. Реакції, які відбуваються у декілька елементарних стадій, називаються складними. До них належать паралельні, консекутивні, спряжені, ланцюгові, послідовно-паралельні та ін.
Шляхии складних хімічних реакцій, в більшості випадків, відбуваються через прості моно- або бімолекулярні реакції.
Паралельними реакціями називаються реакції, в яких вихідна речовина бере участь одночасно в різних реакціях:
k1
  B
A─ k2 B
A─ k2
 D D
|
Прикладом таких реакцій є реакції утворення ізомерів фенолу, бензену при нітруванні нітратною(V) кислотою.
В живих організмах і рослинах глюкоза окиснюється до піровіноградної кислоти, а потім окиснення відбувається двома паралельними шляхами – по циклу Кребса і по циклу гексозомонофосфату.
При нагріванні оксиду нітрогену(ІІ) його розкладання відбувається за двома паралельними реакціями:
 
| N2+O2 | |
| 2NO | ||
| N2O+O |
Для двох паралельних необоротних реакцій першого порядку можна записати:

Кожну з констант швидкості можна визначити, скориставшись рівняннями:
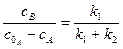
| і | 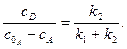
|
Прямі залежності 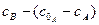 і
і  проходять через початок координат, з кутовими коефіцієнтами, що дорівнюють відповідно:
проходять через початок координат, з кутовими коефіцієнтами, що дорівнюють відповідно:
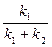
| і | 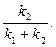
|
Консекутивними або послідовними реакціями називаються хімічні реакції, в яких утворення кінцевого продукту з вихідних речовин відбувається через декілька проміжних стадій:

Проміжний продукт В іноді називається інтермедіатом.
Кінетика послідовних реакцій залежить від співвідношення значень констант швидкості реакцій. На рис.3.11 приведені залежності 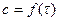 для послідовності двох реакцій першого порядку при
для послідовності двох реакцій першого порядку при 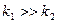 і
і 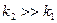 . Значення
. Значення  і
і 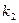 дістають із залежності
дістають із залежності 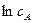 і
і  від
від 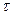 .
.
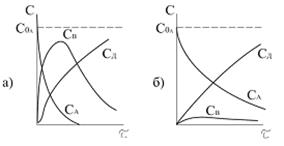
|
Рис.3.11. Зміна концентрацій речовин А, В і D залежно
від часу: а - 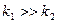 і б - і б - 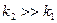
|
При незначній відмінності між реакційною здатністю реагентів А і В, тобто коли 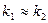 , характер швидкості зміни концентрацій речовин А, В і D в ході реакцій приведено на рис.3.12.
, характер швидкості зміни концентрацій речовин А, В і D в ході реакцій приведено на рис.3.12.
Як бачимо, початкова швидкість зміни концентрацій для речовин А і В максимальна. Зменшення  характеризує кут нахилу прямої
характеризує кут нахилу прямої  . Кути нахилу кривої залежності
. Кути нахилу кривої залежності 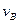 від
від 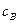 на початковій і кінцевих стадіях відповідають відповідно
на початковій і кінцевих стадіях відповідають відповідно  і
і 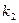 . Час, при якому
. Час, при якому 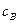 стає максимальним, визначають за рівнянням:
стає максимальним, визначають за рівнянням:
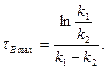 (3.49)
(3.49)
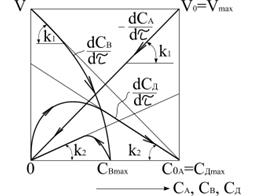
|
Рис.3.12. Залежність 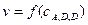 для двох послідовних
реакцій першого порядку при для двох послідовних
реакцій першого порядку при 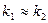
|
На початку реакції концентрація 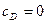 , а на кінцевій стадії кут нахилу кривої
, а на кінцевій стадії кут нахилу кривої 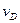 від
від 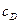 дорівнює
дорівнює 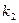 .
.
За механізмом послідовних реакцій відбуваються такі біологічні процеси, як гідроліз глікогену, гідроліз АТФ та ін.
Спряжені реакції – це хімічні реакції, в яких одна реакція відбувається тільки в присутності іншої. У біохімії такі реакції називають тандемними.
Прикладом спряженої реакції є реакції окиснення сульфату феруму(ІІ) пероксидом гідрогену:
 (І)
(І)
Одночасно з окисненням сульфату феруму(ІІ) відбувається і окиснення йодиду гідрогену:
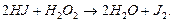 (ІІ)
(ІІ)
Самостійно окиснення йодиду гідрогену пероксидом гідрогену не відбувається, але в присутності сульфату феруму(ІІ), що окиснюється, окиснюється і йодид гідрогену.
В цієї спряженої реакції сульфат феруму(ІІ) є індуктором тому, що він індукує реакцію ІІ, а йодид гідрогену – акцептор. Сполуку пероксид гідрогену, яка є загальною для обох реакцій, називають актором.
Схематично спряжені реакції позначають:
 (І)
(І)
 (ІІ)
(ІІ)
де А – актор, В – індуктор, С – акцептор.
Ланцюгові реакції. Ланцюговий характер мають хімічні реакції, які перебігають за участю вільних атомів, радикалів, молекул, хімічно активних частинок, що мають надлишок енергії.
Приклади ланцюгової реакції є реакція утворення хлориду гідрогену з Гідрогену і Хлору:
1. 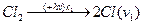 Ініціювання, де hv - квант світла.
Ініціювання, де hv - квант світла.
2. 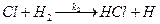
3.  (v2 і v3) Зростання ланцюга.
(v2 і v3) Зростання ланцюга.
4.  (v4) Перенос ланцюга.
(v4) Перенос ланцюга.
5.  (v5) Обрив ланцюга.
(v5) Обрив ланцюга.
За ланцюговим механізмом відбувається галогенування алканів:
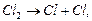
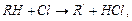
 і т.д.,
і т.д.,
радіоактивне перетворення різних ізотопів:
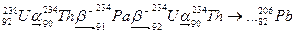
| тощо. |
Послідовно-паралельні хімічні реакції – це реакції, в яких одна з вихідних речовин бере участь як в реакціях утворення, так і в реакціях витрачання проміжних речовин. Типова схема таких реакцій має вигляд:
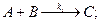

.............................
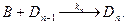
Кінетика ферментативних реакцій. Каталітична дія ферментів поділяється на три стадії: приєднання молекули субстрату (S) до ферменту (F); перетворення субстрату; відділення кінцевих продуктів реакції (R) від ферменту:
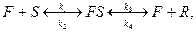 (3.50)
(3.50)
де k1, k2, k3 i k4 – константи швидкості двох прямих і двох зворотніх реакцій.
За числом учасників ферментативних реакцій їх поділяють на одно- і двосубстратні. Найбільш поширені двосубстратні реакції з утворенням двох продуктів:
A + B L R1 + R2.
Односубстратні реакції є мономолекулярними і відносяться до реакцій першого порядку. Більшість бімолекулярних реакцій є реакціями другого порядку. Їх швидкість пропорційна концентрації двох реагуючих речовин:
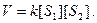
Швидкість ферментативної реакції залежить від активності ферменту. За одиницю будь-якого ферменту розуміють таку кількість ферменту, яка за певних умов ([S], pH, t) каталізує перетворення субстрату із швидкістю 1 моль/с. Ця одиниця називається катал- кат (1 кат = 109 нкат).
Активність ферменту виражають також у стандартних одиницях (кількість ферменту, яка каталізує перетворення 1 мкМ субстрату за 1 хвилину) (1 кат = 6 × 107 стандартних одиниць).
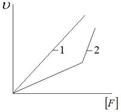
Залежність швидкості реакції від концентрації ферменту, як правило, є лінійною (рис.3.13 а, пряма 1) і порушується при нестачі субстрату чи активатору (крива 2).
Гіперболічний характер залежності V від [S] (рис.3.13 б) свідчить про те, що порядок ферментативної реакції змінюється: на початку це реакція першого порядку, в кінці – нульового, а при проміжних концентраціях субстрату – мішаного порядку.
 а)
а)
|  б)
б)
|
| Рис.3.13. Залежність початкової швидкості (V) реакції від концентрації ферменту (а) і субстрату (б) |
При вивченні кінетики ферментативних процесів Л. Міхаеліс і М. Ментен (пізніше Дж. Бриггс і Дж. Холдейн) розробили теорію кінетики дії ферментів для односубстратної реакції, яку виразили через рівняння:
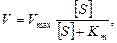 (3.51)
(3.51)
де Vmax – максимальна швидкість за умов насичення ферменту субстратом; Km – константа Міхаеліса, яка дорівнює:
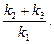
Константа Міхаеліса  чисельно дорівнює концентрації субстрату, при якій швидкість ферментативної реакції досягає половини свого максимального значення Vmax (рис.3.13, б).
чисельно дорівнює концентрації субстрату, при якій швидкість ферментативної реакції досягає половини свого максимального значення Vmax (рис.3.13, б).
Рівняння (3.51) дійсно описує кінетичні данні рисунку (3.13, б). Так, при низьких концентраціях субстрату тобто, коли
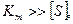
швидкість реакції прямо пропорційна концентрації субстрату і описується рівнянням першого порядку

При високих концентраціях субстрату, коли
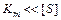
швидкість реакції максимальна і не залежить від концентрації субстрату
V =Vmax (реакція нульового порядку).
Якщо рівняння Міхаеліса-Ментена представити у вигляді подвійних обернених величин одержимо:
 (3.52)
(3.52)
Графічна залежність 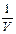 від
від 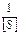 є прямою, яка відсікає на осі ординат відрізок
є прямою, яка відсікає на осі ординат відрізок 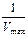 , а на осі абсцис -
, а на осі абсцис -  (рис.3.14, а).
(рис.3.14, а).

| 
| 
|
| а) б) в) | ||
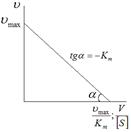
| Рис.3.14. Залежність оберненої швидкості від оберненої концентрації субстрату (а) [S]/V від [S] (б) і V від V/[S] (в) для визначення km i Vmax |
Кут нахилу її дорівнює:

Перетворюючи рівняння (3.52) дістанемо нове лінійне рівняння:

яке використовують для графічного визначення 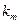 (рис.3.14, б). На осі абсцис пряма відсікає відрізок, який відповідає значенню -
(рис.3.14, б). На осі абсцис пряма відсікає відрізок, який відповідає значенню - 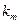 , а на осі ординат -
, а на осі ординат - 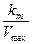 . Кут нахилу прямої дорівнює:
. Кут нахилу прямої дорівнює:

Якщо помножити обидві частини згаданого рівняння на Vmax це дає ще один вид рівняння, графік якого являє собою пряму лінію (рис.3.14, в). За кутом нахилу прямої можна визначити значення константи Міхаеліса 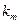 .
.
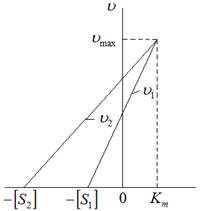
Для визначення  і Vmax використовують також лінійний графік, для побудови якого не потрібні розрахунки, тому що кожна пряма відповідає одному спостереженню (рис.3.15):
і Vmax використовують також лінійний графік, для побудови якого не потрібні розрахунки, тому що кожна пряма відповідає одному спостереженню (рис.3.15):

|
| Рис.3.15. Залежність Vmax від km |
У кінетиці ферментативних реакцій значну цікавість представляють механізми їх гальмування речовинами, які перешкоджають утворенню фермент – субстратного комплексу. Такі речовини називають інгібіторами.
За механізмом реакцій з ферментами інгібітори поділяються на дві великі групи: інгібітори (І), які вступають з ферментом у необоротну реакцію:

і інгібітори, які реагують з ферментом необоротно:

де FI - фермент – інгібіторний комплекс, який не перетворюється у продукт;  - константа гальмування, яка показує спорідненість інгібітору до ферменту:
- константа гальмування, яка показує спорідненість інгібітору до ферменту:

Для необоротного гальмування  дорівнює нулю.
дорівнює нулю.
Розрізняють три типи оборотного гальмування ферментів: конкурентне, неконкурентне і безконкурентне.
Конкурентними інгібіторами називають інгібітори, які взаємодіють з тими же функціональними групами активних центрів ферментів, з якими в ході реакції взаємодіють субстрати.
Неконкурентний інгібітор зв’язується з ферментом поза активним центром. Приєднання такого інгібітору знижує активність ферменту, а не його спорідненість до субстрату.
Безконкурентний інгібітор оборотно взаємодіє з ферментом тільки після утворення фермент-субстратного комплексу:
FS + I L FSI.
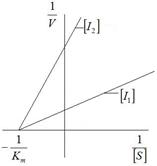
У практиці зустрічаються випадки змішаного гальмування, коли один і той же інгібітор може реагувати з вільним субстратом в різних точках, а також з фермент-субстратним комплексом у різних стадіях його перетворення. Тип гальмування може бути виявлений шляхом побудови графіків Лайнуівера – Берка (рис.3.16).
 а)
а)
|  б)
б)
|
| Рис.3.16. Графіки Лайнуівера – Берка для конкурентного (а) і неконкурентного (б) гальмування |
Як випливає з графіків присутність конкурентного інгібітора не змінює значення  ,
,  при цьому збільшується. Для неконкурентного гальмування константа
при цьому збільшується. Для неконкурентного гальмування константа  не залежить від концентрації субстрату, а для
не залежить від концентрації субстрату, а для  спостерігається його зниження.
спостерігається його зниження.
На швидкість ферментативних реакцій впливає як температура, так і pH середовища. Температурний оптимум для більшості ферментів знаходиться в межах 40 – 600 С. При температурі 80 – 1000 С ферменти, що мають білкову природу, необоротно денатурують. Проте, слід відмітити, що відомі термофільні організми, які існують при температурі 100 – 2000 С.
Ферментативні реакції чутливі до зміни рН середовища. Це пов’язано з наявністю у ферментів великої кількості йоногенних груп.
Значення рН, при якому швидкість реакції максимальна, називається оптимумом рН.
Графічна залежність швидкості більшості ферментативних реакцій від температури і рН має дзвіновидну форму (рис.3.17).
|
|
|
|
|
Дата добавления: 2015-05-23; Просмотров: 1084; Нарушение авторских прав?; Мы поможем в написании вашей работы!