
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тема 5. Фізико-хімія поверхневих явищ. Адсорбція
|
|
|
|
Поверхневі явища і їх значення. В любих гетерогенних системах, особливо у високодисперсних, природа межи між частинками дисперсної фази і дисперсійним середовищем, молекулярна будова межі поділу і фізико-хімічні взаємодії, що відбуваються на ній, визначають багато чисельні явища і процеси, які характерні для заданої системи.
Вивчення поверхневих явищ відкриває шляхи регулювання цих явищ і взаємодію у природі, а також регулювання ними у техніці.
Керування фізико-хімічними явищами на межі поділу дисперсних фаз дозволяє вирішити такі задачі, як закріплення грунтів (зниження їх осідання і утворення плавунів), тонко регулювати процеси структуроутворення в глинистих суспензіях, які застосовують при свердлуванні, забезпечувати рухливість і незлипання ниток, коли їх прядуть, знижувати водопотребу цементних розчинів і маслопотребу фарб, або, наприклад, забезпечувати добру адгезію бітуму до гравію, щебеню в асфальтобетоні.
На межі поділу фаз у живому організмі і рослинах відбуваються біохімічні процеси обміну і синтезу речовин, ферментативні реакції і інші процеси, які пов’язані з життєдіяльністю організмів і рослин.
Дисперсність. Питома поверхня і вільна поверхнева енергія. Дисперсність – характеристика розмірів частинок в дисперсних системах. За міру дисперсності речовини прийнято ступінь дисперсності 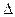 . Це величина, обернена розміру (діаметру) часточки d:
. Це величина, обернена розміру (діаметру) часточки d:
 , (м-1). (5.1)
, (м-1). (5.1)
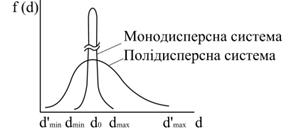
Дисперсність полідисперсних систем характеризується функцією розподілення маси (об’єму) частинок за їх розміром f(d) (рис.5.1). Крім того, вони характеризуються ще і ступенем полідисперсності, тобто розмірністю кривої розподілу – її основою d’min – d’max – повним інтервалом частинок і їх ймовірним діаметром d0.
Розмір частинок визначає також іншу, дуже важливу характеристику дисперсної системи – питому поверхню SПИТ:
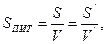 (м-1) (5.2)
(м-1) (5.2)
де S і V – відповідно сумарні поверхня і об’єм дисперсної фази; S’ і V’ – поверхня і об’єм одної часточки.
|
| Рис.5.1. Диференціальні криві розподілу частинок за їх розміром (d0 – ймовірний діаметр) |
Кількість співвідношення між  і SПИТ для часточок різних форм залежать тільки від розміру часточок. Наприклад, часточка сферичної форми (куляста) характеризується розміром діаметру d (табл. 5.1). Для неї:
і SПИТ для часточок різних форм залежать тільки від розміру часточок. Наприклад, часточка сферичної форми (куляста) характеризується розміром діаметру d (табл. 5.1). Для неї:

SПИТ в табл.5.1 відповідає умові диспергування при збереженні форми і дворазового зменшення розмірів часточок.
Величина питомої поверхні систем, наприклад, із куль одного розміру діаметром 1 мм SПИТ = 6 . 103 м-1, для часточок розміром 1 нм SПИТ = 6 . 109 м-1. Загальна поверхня 1 м3 дисперсної фази таких часточок (1 нм) становить 6000 км2.
Велика міжфазна поверхня, яка притаманна дисперсним системам, визначає особливо важливу роль, яку грають в них явища, що відбуваються на межі поділу фаз, - поверхневі явища.
Таблиця 5.1
Співвідношення між 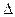 і SПИТ різних форм часточок
і SПИТ різних форм часточок
| Назва час-тинки | Форма частинки | SПИТ | Назва час-тинки | Форма час-тинки | SПИТ |
| Куляста | 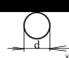
| 6Δ | Двовіс-нови-тягну-ті (плас-тинки, луски) | 
| 2Δ |
| Кубічна | 
| 6Δ | Агре-гати |
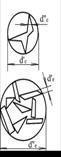
|
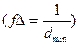
|
| Одновіс-новитяг-нуті (паличко-подібні, голкопо-дібні) | 4Δ | (Врахову-ється ступінь анізомет-ричності А
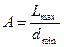
|
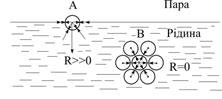
Дві фази, наприклад рідина і пара в однокомпонентній системі, можуть існувати в рівновазі тільки при наявності стійкої межі поділу між ними. Міжмолекулярні взаємодії молекул в площині фаз і в об’ємі рідкої фази (рис.5.2) істотно відрізняються за енергіями.
|
| Рис.5.2. Молекулярні сили, які діють на молекули у поверхневому шарі та в об’ємі рідини (R – рівнодіюча сил молекулярної взаємодії) |
Молекула А, що міститься у поверхневому шарі на межі поділу фаз, перебуває під впливом молекулярних сил взаємодії з боку прилеглих до неї молекул, які розміщені як на поверхні поділу фаз, так і знизу під нею. Положення таких молекул енергетично нескомпенсоване (R >> 0). Якщо молекула знаходиться в об’ємі рідкої фази (В), вона рівномірно притягається з усіх боків такими же за природою молекулами. Силове поле міжмолекулярної взаємодії в цьому випадку повністю зрівноважується (R=0).
Таким чином, поверхневі молекули мають надлишкову енергію. Ця енергія може перетворюватись на роботу, яка витрачається на переміщення молекул з поверхні поділу фаз у глибину рідини.
Такий надлишок енергії називають вільною поверхневою енергією  . Відповідна величина, віднесена до одиниці поверхні, називається питомою вільною поверхневою енергією
. Відповідна величина, віднесена до одиниці поверхні, називається питомою вільною поверхневою енергією  . Її можна розглядати як силу, яка протидіє збільшенню площі поверхні. Існування цієї сили наочно ілюструє дослід Дюпре (рис.5.3).
. Її можна розглядати як силу, яка протидіє збільшенню площі поверхні. Існування цієї сили наочно ілюструє дослід Дюпре (рис.5.3).

|
| Рис.5.3. Схема досліду Дюпре |
По каркасній рамці з дроту (шириною L) вільно переміщується легка планка. Перевернутий каркас занурюють в мильний розчин з гліцерином. Прилад виймають і повертають в попереднє положення. При цьому між каркасом і планкою утворюється двобічна плівка з мильного розчину (заштрихована площа). На петлю в планці підвішують вантаж під дією якого планка опускається і розтягує мильну плівку. Робота, яка при цьому витрачається дорівнює:

де Р – вага вантажу; dh – відстань, на яку перемістилась планка. Площа, на яку збільшилась поверхня плівки, становить:
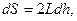
де множник „2” відповідає двобічності плівки.
Збільшення вільної поверхневої енергії системи при цьому відбувається на:
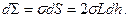 (5.3)
(5.3)
Підставляючи в це рівняння значення dS маємо:
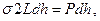
звідки

Таким чином, величина  може розглядатися не тільки як питома поверхнева енергія, але одночасно як сила, яка прикладена до одиниці довжини контуру, що оточує поверхню, і направлена вздовж цієї поверхні перпендикулярно до контуру. Тому, якщо вантаж зняти, то планка займе попереднє положення. Цю стягуючу силу називають поверхневим натягом.
може розглядатися не тільки як питома поверхнева енергія, але одночасно як сила, яка прикладена до одиниці довжини контуру, що оточує поверхню, і направлена вздовж цієї поверхні перпендикулярно до контуру. Тому, якщо вантаж зняти, то планка займе попереднє положення. Цю стягуючу силу називають поверхневим натягом.
Дію поверхневого натягу можна наочно представити у вигляді сукупності сил, що стягують краї поверхні до центру. Ці сили зображені на рис.5.4 стрілочками-векторами; довжина стрілочок відображає величину поверхневого натягу, а відстань між ними відповідає прийнятій одиниці довжини.

|
| Рис.5.4. Схема дії сил поверхневого натягу |
Оскільки питома вільна поверхнева енергія і поверхневий натяг є синонімами відповідно в якості розмірності величини  в рівній мірі використовують як Дж/м2, так і Н/м. Величина
в рівній мірі використовують як Дж/м2, так і Н/м. Величина  є важливою молекулярною константою. Вона характеризує інтенсивність поля молекулярних сил, яка позначається загальним терміном полярність рідини.
є важливою молекулярною константою. Вона характеризує інтенсивність поля молекулярних сил, яка позначається загальним терміном полярність рідини.
Підвищення температури супроводжується пропорційним послабленням сил міжмолекулярної взаємодії, тому при досягненні критичної температури (Т = ТКР)  = 0. В цьому випадку зникає відмінність властивостей співіснуючих рідкої і газоподібної фаз, зникає також її поверхня поділу.
= 0. В цьому випадку зникає відмінність властивостей співіснуючих рідкої і газоподібної фаз, зникає також її поверхня поділу.
Кожна чиста рідина має сталий коефіцієнт поверхневого натягу (при Т = const), величина якого залежить від природи речовини. Він тим більше, чим більша полярність молекул рідини, він також залежить від здатності молекул утворювати водневі зв’язки та ін. Нижче наведені значення поверхневого натягу для деяких рідин на межі з повітрям при 293 К (табл.5.2).
Таблиця 5.2
Поверхневий натяг для деяких рідин на межі з повітрям при 293 К
| Рідина | 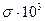 , Дж/м2 , Дж/м2
| Рідина | 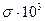 , Дж/м2 , Дж/м2
|
| Вода | 72,7 | Хлороформ | 27,1 |
| Гліцерин | 63,4 | Ацетон | 23,7 |
| Бензен | 28,9 | Етанол | 22,3 |
| Скипидар | 27,7 | n -Гексан | 18,4 |
| Оцтова кислота | 28,8 | Етиловий естер | 17,0 |
З наведених значень поверхневого натягу випливає, що величина поверхневого натягу води в порівнянні з поверхневим натягом інших рідин має найбільшу величину.
У випадку незмішуваних рідин міжфазний натяг розраховують за правилом Антонова:
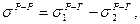 (5.4)
(5.4)
де 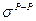 - міжфазний натяг на межі поділу першої рідини у другій, та другої у першій;
- міжфазний натяг на межі поділу першої рідини у другій, та другої у першій; 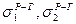 - поверхневий натяг на межі з газовою фазою рідини 2 у рідині 1 та рідини 1 у рідині 2 відповідно.
- поверхневий натяг на межі з газовою фазою рідини 2 у рідині 1 та рідини 1 у рідині 2 відповідно.
З термодинаміки випливає, що будь яка гетерогенна система прагне зменшити поверхневу енергію:


за рахунок зменшення або  , або S.
, або S.
Зменшення  досягається поглинанням або розчиненням поверхневим шаром часточок дисперсної фази, речовин із середовища. Поверхня поділу фаз зменшується за рахунок утворення міжчасткових контактів, переносу речовини з малих часточок на більші.
досягається поглинанням або розчиненням поверхневим шаром часточок дисперсної фази, речовин із середовища. Поверхня поділу фаз зменшується за рахунок утворення міжчасткових контактів, переносу речовини з малих часточок на більші.
Отже, наявність у міжфазних шарів надлишкової вільної енергії приводить до різноманітних явищ (змочування, адгезії, адсорбції тощо).
Когезія та адгезія. Когезія (зчеплення) – притягання між молекулами (атомами і йонами) в об’ємі даного тіла. Речовини в конденсованому стані (тверді і рідкі тіла) характеризуються високою когезією, а газоподібні – дуже малою когезією. Когезія характеризує ідеальну міцність тіла, що визначається силою зчеплення утворюючих його молекул, атомів, йонів.
Для отримання зв’язку поверхневої енергії з енергією зчеплення молекул в об’ємі конденсованої фази введена величина WК, яка називається роботою, або енергією когезії. Ця величина може бути визначена як робота, яку необхідно здійснити в оборотному ізотермічному процесі розділення на дві частинки стовпчика одиничного перерізу. Оскільки в такому процесі утворюються дві поверхні одиничної площі, робота когезії дорівнює подвійному значенню поверхневого натягу:
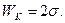 (5.5)
(5.5)
За мікроскопічною теорією Гамакера і Де-Бура роботу когезії визначають як результат підсумовування дисперсійних взаємодій між молекулами, які містяться в двох полунескінченних об’ємах конденсованої фази, що розділені плоским перерізом шириною h (рис.5.5).
Об’єм 2 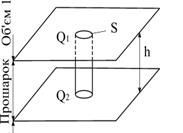
|
| Рис.5.5. Схема, яка ілюструє когезію |
Величина енергії взаємодії фаз Umol дорівнює енергії взаємодії молекул, що знаходяться в нескінченно довгому циліндрі одиничного перерізу S над площиною Q1, з молекулами у всьому об’ємі, розташованому над площиною Q2. В цьому випадку роботу когезії розглядають як ту границю, до якої намагається величина Umol при зменшенні товщини перерізу h до розміру молекули b. Таким чином при:

 (5.6)
(5.6)
де А – стала Гамакера (Дж).
WK має місце для любих рідких фаз: полярних і неполярних. Її називають ще когезійною міцністю, або міцністю на розрив.
Так, когезійна міцність для води при 298 К складає:
 Дж/м2.
Дж/м2.
Адгезія (прилипання) – молекулярний зв’язок між поверхнями двох різнорідних твердих або рідких тіл (фаз), що стикаються.
Термодинамічною характеристикою адгезії є спад вільної енергії на 1см2 поверхні адгезійного шва в ізотермічному оборотному процесі.
Представимо собі дві конденсовані речовини (2 і 3) з поверхнею 1 см2 на межі з газом (повітрям) (1). Це можуть бути дві рідини або рідина і тверде тіло: 
При суміщенні цих поверхонь, тобто нанесенні одної речовини на другу, відбувається адгезія. Так як система залишається двофазною, то залишається і міжфазний натяг (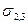 ). В цьому процесі початкова енергія Гіббса зменшиться на величину, яка дорівнює роботі адгезії, тобто:
). В цьому процесі початкова енергія Гіббса зменшиться на величину, яка дорівнює роботі адгезії, тобто:
 . (5.7)
. (5.7)
Енергія Гіббса для вихідного і кінцевого станів дорівнює:
 і
і 
де 
 відповідно поверхневі натяги другого і третього конденсованих тіл з газом (повітрям) і міжфазний натяг на межі другого тіла з третім. Тоді
відповідно поверхневі натяги другого і третього конденсованих тіл з газом (повітрям) і міжфазний натяг на межі другого тіла з третім. Тоді

або
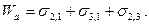 (5.8)
(5.8)
Величина Wа характеризує спорідненість контактуючих фаз, тобто ступінь насичення нескомпенсованих поверхневих сил при контакті; навпаки, міжфазна енергія 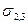 визначає інтенсивність залишкових нескомпенсованих взаємодій на межі поділу конденсованих фаз.
визначає інтенсивність залишкових нескомпенсованих взаємодій на межі поділу конденсованих фаз.
На відміну від когезії, коли робота витрачається на подолання сил зчеплення між однорідними молекулами, робота адгезії Wа пов’язана з енергією взаємодії різнорідних молекул (атомів).
Змочування та розтікання. Якщо на поверхню твердого тіла нанести краплину рідини, то у такої системи присутні три різних поверхні поділу фаз: між рідиною і твердим тілом, рідиною і парою (повітрям) і твердим тілом і парою з поверхневим натягом  відповідно. Краплина рідини на поверхні твердого тіла представляє собою шаровий сегмент з висотою Н, радіусом кривизни r і радіусом кола трьохфазного контакту (периметр змочування) r1 (рис.5.6, а).
відповідно. Краплина рідини на поверхні твердого тіла представляє собою шаровий сегмент з висотою Н, радіусом кривизни r і радіусом кола трьохфазного контакту (периметр змочування) r1 (рис.5.6, а).

|
| Рис.5.6. Взаємодія краплини рідини з поверхнею твердого тіла: а) змочування; б) незмочування |
Лінія перетину усіх трьох поверхонь поділу називається лінією змочування (замкнута лінія змочування утворює периметр змочування). Кут 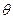 між поверхнями рідина-пара і тверде тіло-рідина називається крайовим кутом змочування.
між поверхнями рідина-пара і тверде тіло-рідина називається крайовим кутом змочування.
У випадку, коли краплина рідини нанесена на іншу рідину схема взаємодії з поверхнями буде мати вигляд (рис.5.7).

|
| Рис.5.7. Рівновага трьохфазної системи фаз (Ф2) – рідина 1 (Ф1) – рідина 2 (Ф3) на межі поділу фаз |
Розглядаючи поверхневі натяги як сили, що прикладені перпендикулярно до одиниці довжини периметру змочування і що діють по дотичній до відповідних поверхонь (рис.5.6, а) можна записати умову рівноваги цих сил:

або 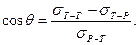 (5.9)
(5.9)
В залежності від значень крайового кута змочування розрізняють такі випадки:
1)  - поверхня змочується (або частково змочується);
- поверхня змочується (або частково змочується);
2) 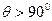 - поверхня не змочується (або погано змочується);
- поверхня не змочується (або погано змочується);
3) крайовий кут змочування не встановлюється – повне змочування поверхні, або розтікання.
У відповідності з рівнянням Юнга (5.9) 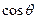 або змочуванню відповідає умова
або змочуванню відповідає умова  (рис.5.6, а), незмочуванню -
(рис.5.6, а), незмочуванню - 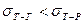 (рис.5.6, б), а розтіканню -
(рис.5.6, б), а розтіканню -  .
.
Рушійна сила процесу розтікання називається роботою розтікання WР (або коефіцієнтом розтікання). Величина WР дорівнює:

Робота розтікання може бути визначена як різниця робот адгезії і когезії:
 (5.10)
(5.10)
Таким чином, добре змочування і розтікання можливі при великій роботі адгезії і при низькій роботі когезії.
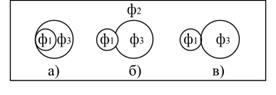
Якщо трьохфазна система складається із трьох рідких фаз, що не змішуються, можливі наступні випадки (рис.5.8):
|
Рис.5.8. Можливі випадки контакту крапель рідини (фази 1 і 3) в рідкої фази 2 при  : а – повне змочування; б – часткове змочування; в – незмочування : а – повне змочування; б – часткове змочування; в – незмочування
|
Повне змочування одної рідини в другій (а), часткове змочування цих рідин (б) і коли рідини не змочуються (в).
Якщо 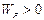 , то рідина буде розтікатися по поверхні, тому що цей процес супроводжується зменшенням вільної поверхневої енергії і відбувається самодовільно. У табл.5.3 наведені приклади, які пояснюють сказане.
, то рідина буде розтікатися по поверхні, тому що цей процес супроводжується зменшенням вільної поверхневої енергії і відбувається самодовільно. У табл.5.3 наведені приклади, які пояснюють сказане.
Таблиця 5.3
Коефіцієнти розтікання для деяких систем
| Система |  , Дж/м2 , Дж/м2
| 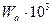 ,
Дж/м2 ,
Дж/м2
| 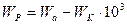
|
| Бензен-бензен Бензен- вода | 57,8 | 65,2 | +7,4, тобто бензен розтікається по воді |
| Сульфур-карбонат-сульфур-карбон Сульфур-карбон-вода | 62,8 | 5,8 | -7,0, тобто сульфур-карбон не розтікається по воді |
У відповідності з (5.10) вуглеводи і інші органічні речовини з малим поверхневим натягом добре змочують практично усі тверді тіла.
Вода-рідина з високою роботою когезії – добре змочує оксиди і розтікається на деяких силікатах, але не змочує флюорорганічні полімери, парафін. В першому випадку ці поверхні гідрофільні, а в другому – гідрофобні по відношенню до полярних молекул води.
При вибірковому змочуванні, тобто коли кожна з рідин окремо змочує поверхню, встановлюється такий крайовий кут, який відповідає доброму змочуванню тією рідиною, спорідненість якої з цією твердою поверхнею більше. Якщо вода добре, ніж карбон гідроген, вибірково змочує поверхню, тобто  , то поверхню називають гідрофільною (олеофобною); якщо поверхня добре змочується неполярним карбонгідрогеном, тобто
, то поверхню називають гідрофільною (олеофобною); якщо поверхня добре змочується неполярним карбонгідрогеном, тобто 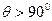 , то таку поверхню твердого тіла називають гідрофобною (олеофільною).
, то таку поверхню твердого тіла називають гідрофобною (олеофільною).
До речовин з гідрофільною поверхнею відносяться: кварц, скло, оксиди, гідроксиди металів окисненні мінерали та ін. До гідрофобних об’єктів відносяться карбонгідрогени, флюориди, листя рослин, хітиновий покрив комах, шкіра тварин тощо.
Важливою кількісною характеристикою енергетики змочування є теплота змочування – кількість енергії, що виділяється при змочуванні одиниці поверхні твердого тіла. Тому, що ентальпія поверхневого шару на межі тверде тіло-газ більше, ніж на межі тверде тіло-рідина, то при змочуванні завжди виділяється тепло, яке дорівнює різниці повних поверхневих енергій або ентальпій шарів після змочування (Н2) і до нього (Н1):
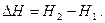
Теплота змочування залежить від кількості рідини, що насичена на поверхні того чи іншого тіла. Це обумовлено проникненням поля поверхневих явищ всередину на певну глибину, яка дорівнює товщині поверхневого шару у фазі рідини.
На змочування твердих тіл рідинами великий вплив здійснює стан поверхні твердого тіла, а саме його шорсткість (кривизна поверхні). Згідно Дерягіну, у випадку контакту рідини з поверхнею реального твердого тіла вираз роботи адгезії необхідно записати у вигляді:
 (5.11)
(5.11)
де 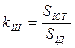 - коефіцієнт шорсткості;
- коефіцієнт шорсткості;  і
і 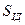 - реальна і ідеальна поверхня твердого тіла.
- реальна і ідеальна поверхня твердого тіла.
Капілярність. Для високодисперсних систем характерна велика кривизна поверхні поділу фаз (шорсткість), тому необхідно враховувати її вплив при розгляданні термодинамічних властивостей таких систем.
Розглянемо поведінку рідини у тонкому капілярі, який занурений в рідину. В цьому випадку можна рахувати, що меніск має сферичну форму (рис.5.9). При умові змочування рідиною стінок капіляру ( ) її поверхня буде викривленою з від’ємним радіусом кривизни r (вгнутий меніск). Внаслідок вгнутої поверхні меніска тиск на нього з боку атмосфери зменшується на силу
) її поверхня буде викривленою з від’ємним радіусом кривизни r (вгнутий меніск). Внаслідок вгнутої поверхні меніска тиск на нього з боку атмосфери зменшується на силу 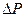 , яка дорівнює:
, яка дорівнює:
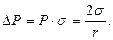 (5.12)
(5.12)
Величина  - різниця тисків у сусідніх фазах, що розділені викривленою поверхнею, називається капілярним тиском.
- різниця тисків у сусідніх фазах, що розділені викривленою поверхнею, називається капілярним тиском.
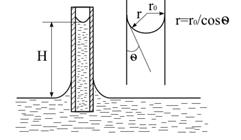
|
| Рис.5.9. Кривизна поверхні рідини і висота капілярного підняття (Н): r0 – радіус капіляра, r – радіус кривизни меніска |
За рахунок 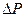 рідина буде підніматися по капіляру до тих пір, поки капілярний тиск не зрівняється з гідростатичним тиском стовпчика рідини, що піднялася в капілярі, тобто
рідина буде підніматися по капіляру до тих пір, поки капілярний тиск не зрівняється з гідростатичним тиском стовпчика рідини, що піднялася в капілярі, тобто
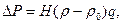 (5.13)
(5.13)
де  і
і 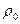 - густина рідини і її насиченої пари (або повітря); Н – висота підйому рідини; q – прискорення сили тяжіння.
- густина рідини і її насиченої пари (або повітря); Н – висота підйому рідини; q – прискорення сили тяжіння.
Радіус кривизни меніска r пов’язаний з радіусом капіляра співвідношенням:

Висота капілярного підняття визначається за формулою Жюрена:
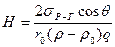 (5.14)
(5.14)
З рівняння (5.14) випливає, що чим краще рідина змочує стінки капіляра, тим вище підняття в ньому при даному значенні  . За цією формулою можна підрахувати, що в капілярі радіусом 0,01 мм при температурі 200С,
. За цією формулою можна підрахувати, що в капілярі радіусом 0,01 мм при температурі 200С,  =72,7.10-3 Дж/м2,
=72,7.10-3 Дж/м2,  , висота підйому біля 1,5 м.
, висота підйому біля 1,5 м.
Капілярні явища мають місце в грунтах. Сукупність капілярів (пор) різних діаметрів в грунті над поверхнею ґрунтових вод утворюють капілярну кайму (рис.5.10). Форма кайми залежить від неоднорідності пор за розмірами. В піщаних грунтах вона більш виразна; при великій нерівномірності пор за розмірами (суглинисті грунти) капілярна кайма розтягнута по висоті. Висота кайми є одною із воднофізичних констант грунту і називається максимальною висотою капілярного підняття hК. Для піщаних грунтів вона складає приблизно 0,4-1 м, супіщаних – 1-1,5 м, суглинистих – 1,5-2,5 м, глинистих – 2,5-5 м.
Характерним проявом капілярного тиску є явище виникнення капілярної стягуючої сили (F) між частинками при наявності меніска (рис. 5.11, а).
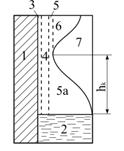
Рис.5.10. Розділ ґрунтової вологі по висоті: 1 – тверда фаза; 2 – ґрунтова вода; 3 – гідроскопічна волога; 4 – плівкова волога; 5 – капілярно-підвищена волога (капілярна кайма); 5а – капілярно-підперта волога; 6 – підвищена волога; 7 – ґрунтове повітря
Величина цієї сили суттєво залежить від кількості рідини в меніску. Наприклад, при висиханні (рис.5.11, а) стягуюча сила максимальна. При збільшенні рідини до утворення циліндричного меніску капілярна стягуюча сила зменшується (рис.5.11, б). Коли утворюється „меніск” з параметрами r=2r0 ця стягуюча сила зникає, тобто F=0 (рис.5.11, в). Власне цим обумовлені факти „розпливання” сильно зволоженого піску і його більш менш доброї формозміни при слабкому зволоженні.

|
| Рис.5.11. Стягуюча сила (F) між частинками при різних станах змочування: а – „зникаючий” меніск, б – циліндричний меніск, в – „меніск” з параметрами r=2r0 |
Капілярні сили в більшості визначають зчеплення частинок і безпосередньо зв’язані з цим зчепленням механічні властивості грунтів, різних технічних, харчових, лікувальних і інших порошків і паст.
Велике значення капілярності має місце в просочуванні рідинами пористих тіл неорганічного походження (піднімання вологи по каменю фундаменту, цеглі). Капілярність відіграє велику роль у зберіганні і переміщення вологі в грунті. Руйнуючи капіляри розпушуванням грунту, припиняють піднімання води на поверхню і уповільнюють висихання грунту. А коткування грунту збільшує прилив вологи на поверхню.
Адсорбція. Прагнення вільної поверхневої енергії (енергії Гіббса) набути мінімально можливого значення може задовольнятися не тільки зменшенням поверхні поділу фаз (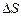 ), а й поверхневого натягу (
), а й поверхневого натягу (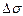 ):
):
 (5.15)
(5.15)
Проходження вільного процесу відбувається за рахунок утворення сферичної і гладкої рідкої поверхні, укрупнення частинок дисперсної фази (зменшення поверхні поділу фаз). До зменшення поверхневого натягу приводять теплові, електричні, фізико-хімічні явища (адсорбція та ін.), що відбуваються на поверхні поділу фаз.
Адсорбція – концентрування речовини (адсорбата) із об’єму фаз на поверхні поділу між ними, наприклад, із газу або розчину на поверхні твердого тіла (адсорбента) або рідини. Адсорбційні сили при фізичній адсорбції мають ту ж саму природу, що і молекулярна взаємодія в газах, рідинах і твердих тілах.
Адсорбція на межі поділу рідина-газ. Адсорбція залежить від природи розчинника і розчиненої речовини, особливо від значень величин поверхневого натягу цих речовин. Якщо поверхневий натяг розчинника, наприклад води, більший від поверхневого натягу розчиненої речовини (органічна речовина),то остання проявляє поверхневу активність, тобто зменшує поверхневий натяг розчину (рис.5.12). Речовини, які зменшують поверхневий натяг межі поділу фаз, називаються поверхнево-активними (ПАР).
ПАР поділяють на аніонні, катіонні, нейонні, амфолітні. Прикладом таких ПАР є карбонгідрогени, ароматичні сполуки, солі жирних кислот, аміни та їх похідні, естери, білки тощо.
ПАР – органічні сполуки дифільної природи. Їх будову та орієнтацію на воді схематично зображують кільцем з зігзагом або рискою (рис.5.13).
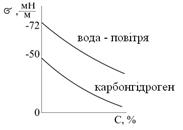
Рис.5.12. Зменшення поверхневого натягу від концентрації розчину на межі поділу вода-повітря і вода-карбонгідроген
Оскільки полярні групи дифільних молекул ПАР мають велику спорідненість до води, тому на межі полярного і неполярного середовища молекули ПАР орієнтуються полярними групами до води, а неполярні (карбонгідрогенний радикал) виштовхуються у газову фазу (повітря).

|
 а)
а)
|
 б)
б)
|
| Рис.5.13. Будова та орієнтація молекул ПАР на межі поділу вода-повітря: а – в розбавлених моношарах (двомірний газ); б – при повному заповненні моношару (конденсований двомірний стан) |
Молекули ПАР мають досить великі, але слабко взаємодіючі між собою неполярні частини, тому завжди:
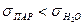 .
.
Внаслідок цього молекули ПАР частково (рис.5.13, а) або повністю (5.13, б) витискують із поверхневого шару полярні молекули води, тобто відбувається адсорбція ПАР. Величина адсорбції дорівнює різниці концентрацій адсорбату в поверхневому шарі і в об’ємі межуючих фаз. Вона позначається літерою Г і вимірюється кмоль/м2.
Механізм процесу адсорбції описує рівняння Гіббса:
 (5.16)
(5.16)
де С – загальна концентрація розчину, моль/м3; R – газова стала 8,314 Дж/моль К; Т – абсолютна температура, К; 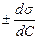 - зміна поверхневого натягу зі зміною концентрації ПАР. Здатність ПАР до адсорбції визначається поверхневою активністю G – зміною поверхневого натягу при введенні перших порцій ПАР у розчині:
- зміна поверхневого натягу зі зміною концентрації ПАР. Здатність ПАР до адсорбції визначається поверхневою активністю G – зміною поверхневого натягу при введенні перших порцій ПАР у розчині:
 (5.17)
(5.17)
Визначається G в Дж.м/моль або Н.м2/моль.
Якщо поверхневий натяг розчину зменшується при збільшенні концентрації розчиненої речовини, тобто  , то адсорбція буде мати додатне значення (Г>0). Таку адсорбцію називають позитивною. Навпаки, коли поверхневий натяг збільшується із зростанням концентрації розчиненої речовини (
, то адсорбція буде мати додатне значення (Г>0). Таку адсорбцію називають позитивною. Навпаки, коли поверхневий натяг збільшується із зростанням концентрації розчиненої речовини ( ), то адсорбція буде мати від’ємне значення (Г<0). Таку адсорбцію називають негативною.
), то адсорбція буде мати від’ємне значення (Г<0). Таку адсорбцію називають негативною.
Позитивна та негативна адсорбція має місце в біологічних об’єктах живих організмів і рослин. Завдяки присутності в клітинних і міжклітинних рідинах поверхнево-активних речовин їх поверхневий натяг значно менший, ніж води, а це забезпечує їх проникність крізь біологічні мембрани, підсилює обмін речовин.
Для визначення адсорбції ПАР на межі рідина-газ користуються ізотермою поверхневого натягу (рис.5.14, крива 1). До довільно вибраній точці на кривій поверхневого натягу проводять дотичну до перетину її з віссю ординат. Із побудування випливає:
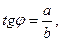 а
а 
звідси 

Рис. 5.14. Залежність поверхневого натягу (1) та
адсорбції (2) від концентрації ПАР на межі рідина-газ
За результатами декількох обчислень будують ізотерму адсорбції (рис.15.14, крива 2).
Аналіз ізотерми абсорбції свідчить, що при низьких концентраціях адсорбція пропорційна концентрації, а при високих концентраціях досягає свого граничного значення (Гmax) і потім не змінюється.
Досліджуючи залежність поверхневого натягу від концентрації водних розчинів органічних речовин біолог Дюкло і фізіолог Траубе встановили правило: поверхнева активність дифільних сполук у водних розчинах однакової концентрації збільшується у 3-3,5 разів зі збільшенням довжини карбонгідрогенного радикалу на одну – СН2 -групу, тобто
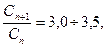
де n – число атомів Карбону в радикалі.
Як видно з рис. 5.15, на якому зображені криві  для ряду водних розчинів насичених органічних кислот, співвідношення значень поверхневого натягу при однаковій концентрації для цього ряду приблизно однакове, тобто
для ряду водних розчинів насичених органічних кислот, співвідношення значень поверхневого натягу при однаковій концентрації для цього ряду приблизно однакове, тобто
 і т.д.
і т.д.  3,2.
3,2.

Рис.5.15. Залежність поверхневого натягу від
концентрації водних розчинів кислот
Із правила Дюкло-Траубе випливає, що площа, яка припадає на одну молекулу максимально насиченого ПАР адсорбційного шару, є сталою в межах цього гомологічного ряду, а це можливо тільки при горизонтальному розташуванні карбогенгідрогенних радикалів на поверхні (див.рис.5.13, б).
Для обчислення поверхневого натягу жирних кислот (або інших ПАР) з невеликим числом атомів Карбону (до С8) застосовують рівняння Шишковського (1908 р.):
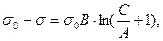 (5.18)
(5.18)
де В – константа (однакова для гомологічного ряду ПАР); 1/A – константа, яка залежить від довжини карбогенгідроненного радикалу.
За допомогою рівняння Шишковського (5.18) можна перейти від рівняння Гіббса (5.16) до рівняння ізотерми адсорбції Ленгмюра, яке має вигляд:
 (5.19)
(5.19)
де Гmax – константа, що характеризує граничну концентрацію речовини в поверхневому шарі (див.рис.5.14); b – константа.
Константу рівняння Ленгмюра можна визначити графічним методом (рис.5.16), перетворивши рівняння Гіббса на рівняння прямої:
 (5.20)
(5.20)
На графіку пряма відсікає на осі ординат відрізок, який дорівнює 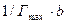 , а тангенс кута нахилу прямої дорівнює
, а тангенс кута нахилу прямої дорівнює  .
.
Досліди Ленгмюра з жирними кислотами (від 14 до 34 атомів Карбону) показали, що незалежно від довжини молекули, площа, яка припадає на 1 молекулу в насиченому моношарі постійна, а це вказує на те, що молекули дійсно орієнтуються вертикально до поверхні (частокол Ленгмюра).

|
| Рис.5.16. Ізотерма адсорбції в координатах С/Г-С |
Разом з тим встановлено, що деякі молекули орієнтуються в адсорбційних шарах горизонтально, а площа, зайнята молекулою, зростає із збільшенням її довжини. Це обумовлено наявністю в молекулах декількох полярних груп.
В таблиці 5.4 наведені величини площі (S) для деяких гомологічних рядів і окремих сполук.
|
|
|
|
|
Дата добавления: 2015-05-23; Просмотров: 2596; Нарушение авторских прав?; Мы поможем в написании вашей работы!