Деформація в тривимірному випадку

Розгляд деформацій у цьому випадку являє собою узагальнення тих міркувань, що були висловлені в двох попередніх розділах.

Зміна вектора зсуву деякої точки пружно деформованого тіла, в залежності від її положення, у просторі, використовується в тривимірному випадку, для визначення дев'ятьох компонентів тензора 2 рангу.

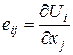; (i, j=1,2,3) (39)

Величини - компоненти тензора відносних зсувів - мають такий фізичний зміст; e₁₁, e₂₂ і e₃₃ - являють собою відносну зміну довжини сторін, паралельних осям 0X ₁, 0X ₂ і 0X ₃ відповідно; e₁₂ являє собою кут повороту сторони елемента об'єму, паралельної осі 0X ₂ у напрямку до 0X ₁ навколо 0X ₃,

e₂₁ дорівнює куту обертання елемента довжини (лінійного елемента), паралельного осі 0X ₁, навколо 0X ₃ у напрямку до 0X ₂.

Аналогічно можна розкрити фізичний зміст інших величин e_ij.

Якщо тіло бере участь в обертальному русі, але деформації в ньому відсутні, то, як ми бачили, тензор відносних зсувів антисиметричний. Виберемо певний початок координат, так, щоб він лежав на вісі обертання. Тоді

U_i = e_ijx_j;

У випадку чисто обертального руху зсув кожної точки перпендикулярно її радіус-вектору. У цьому випадку скалярний добуток радіус-вектора на вектор зсуву дорівнює нулю:

U_ix_i = 0;

Оскільки U_i = e_ijx_j; останнє співвідношення можна записати ще так:

e_ijx_ix_j =0 (40)

Так як (40) справедливо для всіх x_i, коефіцієнти його лівої частини повинні бути рівні нулю. Отже,

e_ij = 0, якщо i = j;

e_ij = -e_ij, якщо i ¹ j;

Але ці співвідношення і являють собою умови антисиметричності тензора e_{ij .} Таким чином, ми ще раз переконуємося в тому, що зсув точок тіла при його обертанні без деформації визначаються антисиметричним тензором 2 рангу.

Тензор деформації в тривимірному випадку, так само, як і у випадку плоскої деформації, являє собою симетричну частину тензора відносних зсувів e_ij

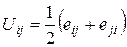
(41)

У розгорнутому записі:

(42)

Діагональні компоненти тензора деформацій являють собою відносні подовження сторін, на яких побудований обраний елемент об’єму. Недіагональні компоненти являють собою деформації зсуву - кути зсуву. Так само, як і у випадку деформації в площині, якщо два лінійних елементи в недеформованому тілі рівнобіжні 0Х ₁ і 0Х ₂, то кут між ними після деформації дорівнює 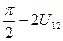. U₂₃ і U₃₁ можуть бути інтерпретовані в такий же спосіб.

Неважко переконатися в тому, що сума діагональних компонентів тензора деформацій являє собою відносну зміну об’єму при деформації.

Щоб переконатися в цьому, розглянемо елемент об’єму у вигляді куба.

До деформації Після деформації

Рис.14. Зміна геометричних розмірів кубічного елемента при всебічному стисненні (розтязі)

Об’єм розглянутого елемента до деформації V, після деформації V +D V.

V = xyz

Зневажаючи членами вищих порядків малості (утримуючих малі величини D x, D y, D z у ступенях вище першої), одержуємо для V +D V;

(43)

Таким чином,

Очевидно, отриманий висновок справедливий для будь-якої декартової координатної системи. Отже сума діагональних компонентів тензора деформації є інваріант тензора U_ik. Це є частковим випадком відомого математичного положення, відповідно до якого сума діагональних компонентів тензора другого рангу є один із трьох інваріантів тензора.

Серед тензорів деформацій різних видів, що відповідають різним станам пружно деформованого тіла, зустрічаються такі, у яких сума діагональних компонентів дорівнює нулю. У цьому випадку, мабуть, деформація відбувається так, що зміна об’єму тіла не має місця. Змінюється при цьому лише форма тіла. Такі деформації без зміни об’єму називаються деформаціями зсуву.

Мал. 15. Деформація зсуву

Іншим "крайнім" випадком є така деформація пружного тіла, при якій відбувається зміна об’єму, але не міняється форма тіла. Така деформація називається всебічним стисненням (розтягом).

Усяку пружну деформацію можна представити у вигляді суперпозиції деформацій чистого зсуву і всебічного стиснення (розтягу).

Це випливає з того, що тензор деформацій завжди можна задати у вигляді суми двох тензорів, один із яких буде відповідати чистому зсуву, а іншій - всебічному стисненню (тобто компоненти першого тензора будуть являти собою деформації чистого зсуву, а другого - деформації всебічного стиснення).

Дійсно, за визначенням, тензор з компонентами U_ik є сумою тензорів з компонентами, якщо виконується рівність:

Нехай

;

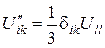
Тоді, мабуть,

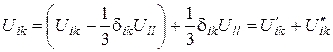(44)

Перший член, 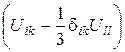являє собою, мабуть, чистий зсув, оскільки сума його діагональних компонентів дорівнює нулю, а виходить, немає зміни об’єму при деформації. Другий член являє собою всебічне стиснення (у широкому розумінні), оскільки зв'язаний тільки лише зі зміною об’єму.

Для того, щоб переконатися, що сума діагональних компонентів тензора 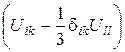дорівнює нулю, необхідно врахувати, що завжди

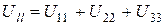
Тоді для суми діагональних компонентів одержуємо:

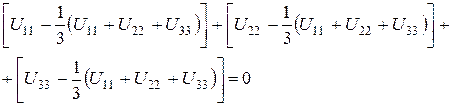
Дата добавления: 2015-05-24