Рівняння теорії пружності

Об'єднаємо в одну систему рівняння рівноваги й узагальнений закон Гука. Рівняння рівноваги (69) (рівність нулю головного моменту системи) вже використано для доказу симетричності тензора напружень, тим самим число шуканих невідомих знижене на три.

Згідно з (87),

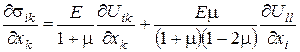
В останньому члені цієї функції у змінної х стоїть індекс ” i ”, тому що, згідно з (87), через наявність у цьому числі, у вигляді співмножника, символу Кронекера, такий член відмінний від нуля лише при k = i.

Оскільки

то

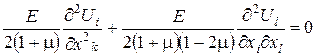(89)

чи

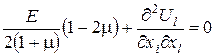(90)

Іноді зустрічається інша форма запису цього рівняння. При цьому користуються, виразом для оператора Лапласа, а також поняттями градієнта функції і дивергенції вектора:

Легко переконатися, що

У цьому випадку три рівності

можна замінити одним векторним співвідношенням

Пам'ятаючи, що

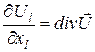
три рівності

також можна замінити однією векторною рівністю

(91)

Тоді рівняння (90) приймає вигляд:

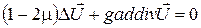
Застосуємо до (91) оператор дивергенції. З огляду на те, що і що, одержуємо:

(92)

Можна встановити, якому диференціальному рівнянню ще більш високого порядку задовольняє вектор деформації. Для цього застосуємо до обох частин рівності (91) оператор Лапласа:

Оскільки, ,

Але згідно з (92).

Таким чином, одержуємо:

(93)

Як ми бачимо, у випадку відсутності об'ємних сил при деформації ізотропного тіла вектор деформації задовольняє бігармонічному рівнянню.

Ми одержали рішення просторової задачі (тобто задачі в трьох вимірах) в переміщеннях: після виключення напружень у нас виявилося три диференціальних рівняння другого порядку (91) (чи три диференціальних рівняння 4 порядку (93)) щодо переміщень - компонентів вектора деформації .

Якби ми захотіли вирішувати задачу в напруженнях, то одержали б 6 диференціальних рівнянь щодо напружень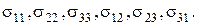

При рішенні задач теорії пружності застосовують той та інший спосіб. При цьому, незважаючи на удавану зручність рішення задач у переміщеннях, з ряду причин більш поширене рішення задач у напруженнях. Не завжди той чи інший спосіб буває чітко виражений. Так, при рішенні задач на площині, коли в рівняннях фігурують тільки дві координати, можна звести задачу до визначення тільки однієї функції, так званої функції напружень, а по ній вже знайти напруження, деформації і переміщення.

2.7. Плоска задача теорії пружності

У плоскій задачі варто розрізняти два випадки: плоский напружений стан і плоску деформацію.

З плоским напруженим станом ми зустрічаємося, якщо дуже тонка пластинка несе навантаження, що прикладене до її контуру і лежить в площині пластинки. При цьому зовнішні поля, унаслідок малої товщини пластинки, варто вважати рівномірно розподіленими по товщині пластинки.

Мал.17. Схема плоского напруженого стану

Внаслідок малої товщини пластинки напруження в ній не можуть помітно змінитися при переході від однієї граничної площини до іншої.

Таким чином, напруження можна вважати рівномірно розподіленими по товщині пластинки і, отже, що вони не залежать від координати Z. Усі явища як би протікають тільки в площині X0Y.

Варто звернути увагу на те, що, хоча в напрямку осі 0Z у розглянутому випадку не діють напруження, унаслідок властивій усім пружним тілам здатності до поперечної деформації, пластина в загальному випадку буде деформуватися в напрямку осі 0Z, і, в залежності від зовнішніх умов, потовщуватись чи потоншуватись. Отже, при плоскому напруженому стані в напрямку осі, перпендикулярної площини пластини, немає напружень, але можливі деформації, тобто точки тіла можуть бути зміщені в цьому напрямку по відношенню до свого первісного положення, до додатка зовнішнього навантаження. Звичайно, кожен атом змістився в напрямку осі 0Z під дією прикладеної до нього сили, але ця сила не є результат безпосередньої дії на атоми зовнішнього напруження, зсув відбувається в результаті того, що всі атоми кристала пружно зв'язані і зсув одних з них у напрямку дії зовнішніх сил призводить до пересування інших у перпендикулярному напрямку.

Плоска деформація має місце, коли пружне тіло в напрямку осі 0Z має, навпаки, велику довжину, поперечні ж перетини тіла в площинах, перпендикулярних цій осі, однакові. При цьому навантаження діють у площинах, паралельних площині X0Y, і не залежать від координати Z. В таких умовах знаходиться, наприклад, довга підпірна стінка, що піддається з боку ґрунту тиску, рівномірному по довжині стінки (мал. 18).

Мал. 18. Приклад задачі, у якій реалізуються умови плоскої деформації

Для розрахунку в цьому випадку ми можемо вирізувати двома нескінченно близькими площинами елемент у вигляді дуже тонкої пластини і досліджувати тільки його, тому що всі інші такі ж елементи будуть знаходитись в однакових умовах (за винятком елементів у країв стінки, що буде враховано в граничних умовах). Таким чином, ми тут знову одержуємо плоску задачу, тому що явище буде протікати в одній площині. Напруження повинні розподілятися рівномірно по товщині пластинки і діяти в площині X0Y.

Однак, цей випадок істотно відрізняється від попереднього (від випадку плоского напруженого стану). Поперечні деформації в напрямку осі Z неможливі, тому що їм перешкоджають сусідні пластинки, що знаходяться в однакових умовах. Це значить, що уздовж осі Z виникають нормальні напруження. Отже, при плоскій деформації в напрямку осі, перпендикулярної площини виділеної пластинки, немає деформацій (переміщень), однак складові напружень уздовж цієї осі, взагалі говорячи, не дорівнюють нулю.

Розглянемо рішення задачі у випадку плоскої деформації.

Запишемо 3 рівняння:

Використаємо спочатку друге з цих рівнянь. Для довільних по координатах від компонентів тензора напружень одержимо співвідношення:

чи

(94)

Одержимо ще одне рівняння. Для зручності будемо шукати рівняння, якому задовольняє сума .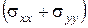

; ;

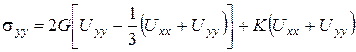
як видно з цих виразів,

,

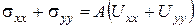де А – деякий коефіцієнт.

Оскільки і , де і 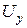- компоненти вектора деформації, то , і ми одержуємо:

;

Оскільки , то з попереднього виразу одержуємо:

;

Таким чином, маємо 3 рівняння:

;

(95)

.

Легко переконатися в тому, що у випадку напруження знаходяться як похідні від деякої функції (так звана функція напружень):

(96)

(97)

Якщо підставити (96) у (95), то побачимо, що при такому зв'язку між напруженнями (компонентами тензора напружень) і функцією перші два рівняння з (95) задовольняються тотожно, а з 3-го рівняння одержуємо:

(98)

Використовуючи, оператор Лапласа, одержуємо:

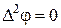(99)

Таким чином, у випадку плоскої деформації рішення задачі вдається звести до одного диференціального рівняння 4 порядку. Розв'язуючи таку задачу, ми повинні підібрати функцію так, щоб вона задовольняла рівнянню (99) і щоб величини 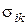задовольняли граничним умовам задачі. Знайшовши таку функцію, ми зможемо застосувати вивчені вище формули для напружень і знайти напруження в будь-якій точці пружного тіла. Знаючи напруження, за законом Гука зможемо знайти деформації і переміщення, функція називається функцією напружень.

Помітимо, що у випадку плоскої деформації напруження 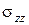визначається через напруження 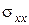і по формулі:

(100)

Це співвідношення випливає зі співвідношення при , що саме відповідає випадку плоскої деформації.

Дата добавления: 2015-05-24