
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тензор напруги
|
|
|
|
ЕЛЕМЕНТИ ТЕОРІЇ ПРУЖНОСТІ І ПРУЖНИХ ВЛАСТИВОСТЕЙ КРИСТАЛІВ.
Змістом теорії пружності є феноменологічний опис деформацій (малих по величині) і напруги у твердих пружних тілах, у тому числі, у кристалах.
Напружений стан тіла можна описати цілком, якщо задати в будь-якій його точці напруги, що діє на нескінченно малій площадці довільної орієнтації. Площадка ця буде характеризуватися одиничним вектором нормалі 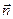 . Вектор напруги позначимо через
. Вектор напруги позначимо через 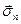 , відзначивши, що, взагалі говорячи,
, відзначивши, що, взагалі говорячи, 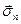 по напрямку не збігається з вектором
по напрямку не збігається з вектором 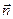 . Індекс n лише вказує орієнтацію площадки, на якій діє розглянута напруга.
. Індекс n лише вказує орієнтацію площадки, на якій діє розглянута напруга.
 |
Ми розглядаємо рівноважний стан і, отже, будь-який елемент об’єму, обраний всередині пружного тіла, знаходиться в стані рівноваги.
Виберемо елемент об’єму так, щоб він був обмежений розглянутою площадкою з нормаллю 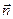 трьома площадками, рівнобіжними координатним осям.
трьома площадками, рівнобіжними координатним осям.
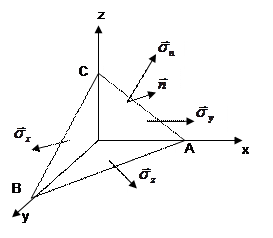
Рис. 8. Результуючі напруги на гранях елемента об’єму.
Напруги 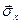 ,
, 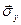 та
та 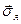 діють на площадках, перпендикулярних координатним осям, але, у загальному випадку, спрямовані не паралельно цим координатним осям.
діють на площадках, перпендикулярних координатним осям, але, у загальному випадку, спрямовані не паралельно цим координатним осям.
Запишемо першу умову статичної рівноваги для обраного тетраедра - рівність нулю головного вектора системи - у випадку, коли силами, що діють на розглянутий об’єм, є лише напруги на його поверхні:

Тут 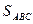 - площа трикутника
- площа трикутника 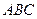 ,
,  ,
, 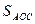 ,
, 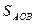 - відповідно площадки трикутників BOC, AOC і AOB. Оскільки зовнішні нормалі до граней BOC, AOC і AOB протилежні по напрямках ортам
- відповідно площадки трикутників BOC, AOC і AOB. Оскільки зовнішні нормалі до граней BOC, AOC і AOB протилежні по напрямках ортам 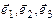 напруги на площадках BOC, AOC і AOB рівні
напруги на площадках BOC, AOC і AOB рівні 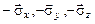 .
.
Очевидно,
SBOC=SABC • 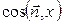 ;
;
SAOC=SABC • 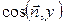 ;
;
SAOB=SABC • 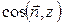 ;
;
Тому остаточно ми одержуємо:
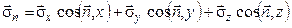 (30)
(30)
Таким чином, виявляється, що досить знати напруги на трьох взаємно перпендикулярних площадках, що проходять через розглянуту точку простору, щоб обчислити напругу на площадці будь-якої орієнтації, що проходить через цю точку.
Кожна з напруг 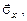
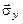 і
і 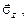 задається трьома числами, що являють собою проекції відповідного вектора на осі обраної координатної системи:
задається трьома числами, що являють собою проекції відповідного вектора на осі обраної координатної системи:
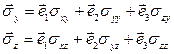 (31)
(31)
чи
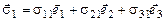
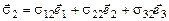
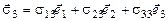
Таким чином, напруга на нескінченно малій площадці будь-якої орієнтації може бути обчислена, якщо в точці, через яку проходить ця площадка, задані дев'ять величин.
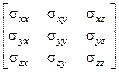 чи
чи 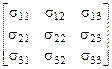 (32)
(32)
Неважко бачити, що ці дев'ять величин являють собою компоненти деякого тензора 2-го рангу.
Зверніть увагу на те, що в (30):
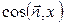 =
= 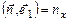 (чи n 1)
(чи n 1)
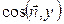 =
= 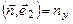 (чи n 2)
(чи n 2)
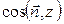 =
= 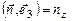 (чи n 3)
(чи n 3)
З врахуванням цього і співвідношень (31), (30) у проекціях на координатні осі запишеться:
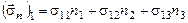 ;
;
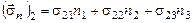 ;
;
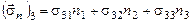 .
.
У скороченій формі запису ці співвідношення виглядають так:
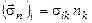
Однак, ми бачимо, що коефіцієнти, що зв'язують лінійним законом компонента двох векторів (у даному випадку, векторів 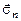 ,
, 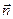 ), є компонентами тензора 2-го рангу. Виходить, 9 величин
), є компонентами тензора 2-го рангу. Виходить, 9 величин 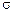 ik – компонента деякого тензора 2-го рангу.
ik – компонента деякого тензора 2-го рангу.
Ми приходимо, таким чином, до висновку, що напружений стан у будь-якій точці пружно деформованого тіла задається тензором 2-го рангу з матрицею
[ 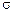 ik]=
ik]= 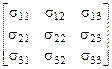 (33)
(33)
Цей тензор називається тензором напруг.
Як ми вже говорили, тензор напруг відноситься до матеріального тензора.
|
|
|
|
|
Дата добавления: 2015-05-24; Просмотров: 419; Нарушение авторских прав?; Мы поможем в написании вашей работы!