Вплив симетрії кристала на його фізичні властивості

Симетрія кристала визначає, якими фізичними властивостями кристал володіє чи може володіти, а якими він ні при яких умовах володіти не може. Наприклад, можна показати, що кристали кубічної симетрії не можуть мати п'єзоелектричні властивості.

Далі, оскільки більшість фізичних властивостей описуються тензорами високих рангів (другого, третього чи четвертого), то для повного визначення деякої властивості необхідне знаходження (шляхом виміру) багатьох величин:

9 – для тензора 2-го рангу

27 – для тензора 3-го рангу.

81 – для тензора 4-го рангу.

Використовуючи знання із симетрії, можна виміривши лише деякі компоненти тензора – властивості, знайти інші шляхом обчислення. Часто буває, що в силу симетрії кристала деякі компоненти тензори-властивості звертаються в нуль. Це також дуже важливо, як для інженерних розрахунків (наприклад, в області твердотілих перетворювачів), так і для визначення кристалічної структури твердих тіл шляхом виміру їхніх фізичних властивостей.

Основою аналізу фізичних властивостей кристалів у залежності від їх симетрії є так називаний принцип Наймана: сукупність елементів симетрії фізичної властивості в даному кристалі повинна включати всі елементи симетрії просторової групи цього кристала.

Таким чином, відповідно до принципу Наймана, симетрія фізичної властивості кристала, у всякому разі, не нижче просторової симетрії кристала.

На принципі Наймана заснований аналіз фізичних властивостей у кристалах, у яких містить у собі наступні основні етапи.

1. Визначення рангу тензора, яким описуєтьсядана фізична властивість.

Наприклад, відомо, що магнітна сприйнятливість твердих тіл зв'язує законом пропорційності вектор намагніченості тіла і вектор магнітного поля, у якому це тіло знаходиться:

(18)

Формула (18) справедлива для ізотропного середовища, а для анізотропного середовища, яким завжди є кристал, те ж саме феноменологічне рівняння, як ми бачили на прикладі закону Ома, приймає вид:

(19)

Переконаємося в тім, що дев'ять величин 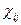являють собою тензор другого рангу.

Уявимо собі, що відбувається перехід від "старої" координатної системи до нової .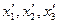

Очевидно, у силу так званого загального принципу відносності, у новій координатній системі закон (19) буде виражатися тими ж співвідношеннями, що й у старій, але входити в них будуть штриховані величини:

(20)

З іншого боку, формула (20) може бути отримана послідовним перетворенням співвідношень (19).

Дійсно,

Порівнюючи останнє співвідношення з (20), знаходимо

Таким чином, дев'ять величин перетворяться по співвідношеннях, які справедливі для компонентів тензора 2-го рангу. Магнітна проникність речовини є тензором другого рангу.

Необхідно до проведеного розгляду зробити одне зауваження, що полегшує подальший розгляд ряду питань.

Очевидно, результат, до якого ми тільки що прийшли, буде виходити всякий раз, коли дев'ять величин входять у виді коефіцієнтів у співвідношеннях типу (19) чи (20), що зв'язують компоненти двох векторів (тензорів 2-го рангу). Дійсно, проведений вище доказ ніде не містив у собі використання того факту, що ми маємо справу саме з магнітною сприйнятливістю речовини, а не з якою-небудь іншою фізичною величиною. Таким чином, коефіцієнт пропорційності, що зв'язує у фізичному законі два вектори, є у загальному випадку, тензором 2 рангу

Розглянемо тепер другий етап аналізу фізичних властивостей кристалів.

2. З'ясування загальних особливостей тензора, що описує аналізовану, фізичну властивість.

Мова йде про те, що з спочатку, звичайно, корисно з'ясувати, чи є розглянутий тензор симетричним (для тензора 2-го рангу), чи антисиметричним (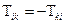 для тензора 2-го рангу), чи може він володіє ще якими-небудь загальними властивостями, загальними в тому змісті, що вони присущи даному тензору завжди, коли він описує визначену фізичну властивість чи середовище поля, але поза залежністю від того, який кристал піддається аналізу.

Такого роду відомості про особливості визначеного тензора дозволяють у багатьох випадках із самого початку знизити в задачі число невідомих – компонентів тензора.

При виконанні цього етапу аналізу фізичних властивостей кристалів намагаються використовувати різні фізичні розуміння, що можуть привести до висновків про математичні властивості тензора. Часто прибігають до розгляду енергії середовища (кристала) підданої такому зовнішньому впливу, при якому поводження системи визначається саме аналізованою фізичною властивістю. Іншим розповсюдженим прийомом є аналіз рівнянь рівноваги і т.д.

Як приклад розглянемо доказ симетричності тензора магнітної проникності (те, що це тензор 2-го рангу випливає безпосередньо з того, що величини входять як коефіцієнти пропорційності в співвідношеннях, що зв'язують компоненти двох векторів і ):

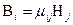(22)

Диференціал енергії магнітного поля виражається, як відомо, формулою

яка являє собою не що інше, як запис у проекціях скалярного добутку векторів і .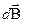

З огляду на те, що 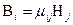одержуємо

; .,

Запишемо цю формулу в розгорнутому вигляді:

Візьмемо похідні першого порядку 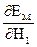і :

=

=

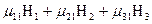
Тепер візьмемо похідні другого порядку 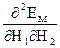і :

=

=

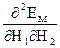Оскільки = ;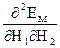

= ;

Аналогічно можна показати, що 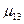= 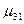і т.д. Таким чином, ми дійдемо висновку, що, = тобто тензор магнітної проникності є симетричним тензором другого рангу.

Третім етапом аналізу фізичних властивостей кристалів є обчислення компонентів відповідних тензорів для кристалів визначеного класу..

3. Обчислення компонентів тензора-властивості для кристалів конкретного класу.

Розглянемо цей етап аналізу на прикладі дослідження тензора другого рангу (тензор провідності).

Розглянемо, наприклад, кристал моноклінної системи , одна вісь симетрії другого порядку, що вибирається звичайно співпадаючої з віссю [вісь Z]). У цьому випадку, як неважко переконатися, обертаються в нуль усі компоненти тензора другого рангу, у яких один індекс збігається з номером осі, рівнобіжної поворотної осі симетрії другого порядку. Дійсно, якщо вісь симетрії другого порядку рівнобіжна осі , матриця перетворення має, очевидно вид:

;

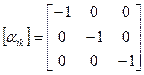Рис. 5. Елементарний осередок ґрат кристала моноклінної системи.

Такий вид матриці перетворень відповідає наступному співвідношенню між "старими" і " новими" координатними осями:

;

;

;

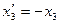Відповідно до закону перетворення компонент тензора другого рангу:

;

;

для даного конкретного випадку одержуємо для 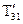, наприклад:

= = = ;

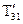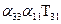Однак, з іншого боку, ми застосували перетворення координат, що відповідає елементу симетрії – осі 2-го порядки. У цьому випадку, нове положення кристала ніяким чином не можна відрізнити від первісного. Отже, у силу властивостей симетрії усі компоненти тензора повинні після перетворення зберегти величину і знак.

Ми приходимо до співвідношень:

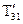= ; =0.

Аналогічним чином можна показати, що повинно виконуватися співвідношення:

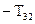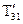= ; = ; =0; =0.

Якщо ж вісь симетрії другого порядку рівнобіжна осі , то обертаються в нуль компонента тензора , , , .

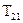Отже, у кристалів моноклінної системи тензор 2-го рангу має лише 5 відмінних від нуля компонентів.

Кристали ромбічної системи мають більш високу симетрію, ніж кристали моноклінної системи (ромбічна чи орторомбічна система 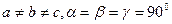). Очевидно, кристал, що відноситься до орторомбічної системи, володіє трьома осями симетрії 2-го порядку, що збігаються з координатними осями. Узагальнюючи на цей випадок попередній висновок, чи попросту повторюючи його для кожної з трьох координатних осей, ми одержимо:

при .

Таким чином, у кристалів ромбічної симетрії відмінні від нуля тільки діагональні компоненти тензора другого рангу: , , . Зокрема, для розглянутого тензора електропровідності відмінний від нуля коефіцієнт , що визначає величину щільності струму уздовж осі 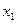, коли поле прикладене уздовж цієї осі, і , що мають аналогічний фізичний зміст для осей і 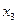відповідно.

У такий же спосіб можна показати, що в кристалів тетрагональної системи теж відмінні від нуля тільки діагональні компоненти тензора другого рангу, але лише два з них є незалежними. Для того, щоб переконатися в цьому, треба врахувати, що в тетрагональній системі завжди є поворотна вісь симетрії 4-го порядку. Припустимо, що координатна система обрана так, що ця вісь симетрії 4-го порядку збігається з віссю 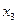(зрозуміло, кінцеві результати фізичного характеру не повинні залежати від того, яка вісь координатної системи сполучена з віссю симетрії 4-го порядку).

Наявність осі симетрії 4-го порядку, що збігається з віссю 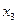, відповідає, очевидно, наступному перетворенню координат, що є перетворенням симетрії:

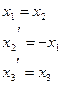чи (23)

Знайдемо матрицю перетворення, що відповідає такому переходу. Як ми знаємо, координати точки, будучи компонентами тензора 1-го рангу, перетворяться по формулах:

У розгорнутому вигляді ці формули являють собою наступні співвідношення:

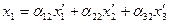
З огляду на співвідношення (23):

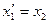
знаходимо, що повинно бути:

Всі інші компоненти матриці перетворення дорівнюють нулю:

Використовуючи формули перетворення для компонентів тензора 2-го рангу знаходимо:

(24)

;

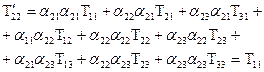
, оскільки, у силу симетрії , ;

Що ж стосується недіагональних елементів, то вони дорівнюють нулю, так само, як для кристалів ромбічної системи, оскільки в розглянутому випадку теж є, природно, три взаємно перпендикулярні поворотні осі симетрії 2-го порядку, що збігаються з координатними осями.

Отже, дійсно, у розглянутому випадку в діагональній матриці тензора 2-го рангу

залишається два незалежних компоненти, наприклад, і .

Усі зроблені для тетрагональної системи висновки щодо компонента тензора другого рангу залишаються справедливими і для кристалів кубічної системи. Однак, у кристалах кубічної системи є ще три поворотні осі симетрії 3-го порядку, що збігаються з просторовими діагоналями куба. Ця обставина приводить до того, що операцією симетрії є циклічна перестановка осей:

Рис. 6. Схема циклічної перестановки осей.

Оскільки , то матриця перетворення

Всі інші доданки пропадають, тому що містять у собі у вигляді співмножників нулі.

Таким чином, 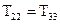. Аналогічно

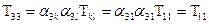
У підсумку маємо:

Тензор, таким чином, задається в розглянутому випадку одним числом. Якщо говорити конкретно про тензор електричної провідності, то встановлений результат може бути сформульований ще так: кристали кубічної симетрії в електричному відношенні ізотропні. Дійсно, уявимо собі, що до кристала прикладене електричне поле , що діє у визначеному напрямку. Складовими поля по координатних осях будуть .

Дата добавления: 2015-05-24