Рівняння рівноваги

Для характеристики напруженого стану в пружно-деформованому тілі необхідно задати тензор напружень. Для опису деформацій треба знайти компоненти тензора деформацій. Таким чином, піддане пружної деформації тіло описується вісімнадцятьма величинами - дев'ятьма компонентами тензора напружень і дев'ятьма компонентами тензора деформацій.

Оскільки тензор деформацій є симетричним тензором 2 рангу, то він має шість незалежних компонентів і загальне число величин, необхідних для опису деформацій і напружень у пружному тілі, скорочується до п'ятнадцяти. П'ятнадцять рівнянь, з яких можна знайти ці величини, являють собою співвідношення, що описують рівновагу довільно обраного об’єму усередині розглянутого тіла, і співвідношення між компонентами тензора деформацій і тензора напружень (так званий узагальнений закон Гука).

Розглянемо співвідношення, що випливають з рівнянь рівноваги. Однак, перш ніж це зробити, нагадаємо поняття дивергенції вектора і дивергенції тензора другого рангу.

Під дивергенцією вектора 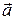розуміється скалярна величина, обумовлена співвідношенням

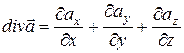(45)

Ця величина - дивергенція вектора - фігурує у відомій формулі теореми Остроградського - Гауса, що у так званій векторній формі має вигляд:

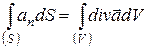(46)

І скалярній формі

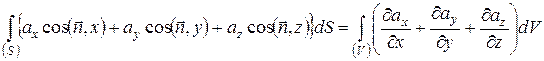(47)

Інтеграл у лівій частині береться по поверхні S, що обмежує об’єм V. 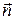- одиничний вектор нормалі до площадки d.

Величина 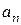визначається виразом:

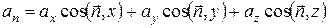(48)

Для будь-якої складової вектора 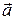по осях X, Y і Z – 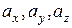- справедливі формули

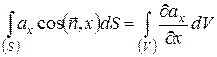
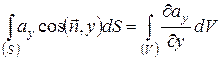(49)

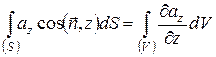
Формули (49) випливають зі співвідношень, одержаних при доведенні теореми Остроградського - Гауса:

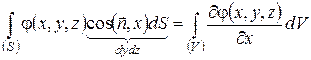
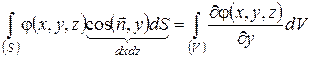(50)

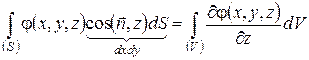
З цих формул легко одержати запис теореми Остроградського - Гауса для будь-якого випадку, оскільки під 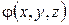можна розуміти будь-яку функцію, у тому числі, будь-яку проекцію вектора.

Помножимо першу формулу з групи (49) на одиничний орт осі 0Х - 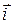другу - на орт осі 0Y - 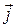, третю на орт осі 0Z - 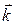. Склавши почленно, одержимо формулу:

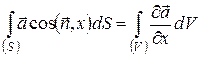(51)

Застосуємо тепер теорему Остроградського - Гауса до трьох векторів, що зв'язані між собою так, що визначають, тензор другого рангу. Нехай ці три вектори - .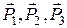

Застосуємо до кожного з них співвідношення типу (51):

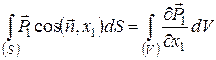
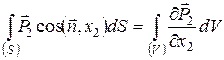
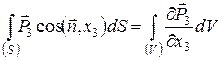
Склавши ці формули, одержуємо:

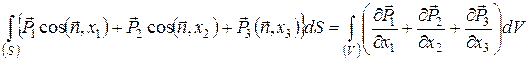(52)

Сума, що стоїть праворуч під знаком інтеграла по об’єму, являє собою деякий вектор, що визначається через компоненти трьох векторів, які разом задають тензор другого рангу. Іншими словами, вектор 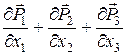задається через компонент 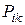тензора другого рангу Õ. Позначимо, за аналогією з дивергенцією вектора (скаляром), вектор 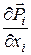дивергенцією

тензора другого рангу Õ:

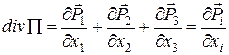(53)

Оскільки

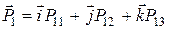
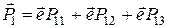
чи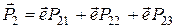

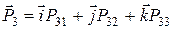
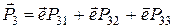
то проекціями вектора 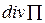є:

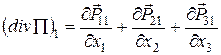
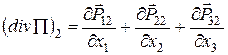
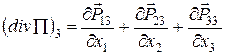
Співвідношення (52) можна тепер переписати у вигляді:

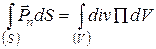(54)

де

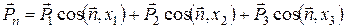(55)

Тепер повернемося до розгляду умов рівноваги довільного об’єму усередині пружно деформованого тіла.

Позначимо через r - густину тіла, через 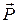– задану зовнішню силу, що діє на одиницю маси (об'ємну силу, результат наявності зовнішнього гравітаційного чи магнітного поля). Через 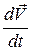позначимо прискорення і через 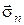- напруження на площадці з нормаллю 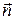. Тоді, за принципом Даламбера, ми можемо записати:

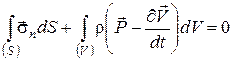(56)

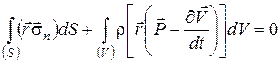(57)

Це - рівняння в найбільш загальному вигляді, для тіл, що деформуються й одночасно рухаються в силовому полі. У більшості випадків висновки теорії пружності використовуються у фізиці при рішенні статистичних задач, коли тіло не рухається і знаходиться поза будь - якими силовими полями, крім гравітаційного. У гравітаційному полі тіло завжди знаходиться в стані спокою, але якщо воно спочиває, 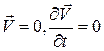, і реакції опор, діючі через поверхню, як і напруження, врівноважують об’ємні сили .

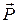У цьому випадку рівняння рівноваги мають вигляд:

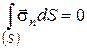(58)

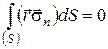(59)

Перше з цих рівнянь являє собою умову рівності нулю головного вектора системи. Друге - умова рівності нулю головного моменту системи.

По узагальненій теоремі Остроградського – Гауса:

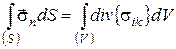
і, отже,

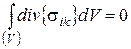
У силу довільності об’єму V з останньої формули випливає:

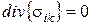(60)

Якщо врахувати, що дивергенцію тензора другого рангу можна виразити через суму часток похідних від трьох векторів, що визначають тензор

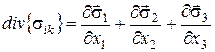
то (60) можна записати у вигляді:

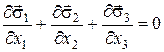(61)

Якщо ж згадати вираз для проекцій дивергенції тензора другого рангу:

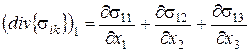
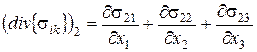
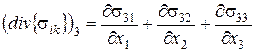
то рівність нулю головного вектора системи може бути записана у вигляді трьох рівнянь:

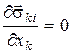(62)

Звернемося тепер до рівняння

.

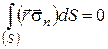Оскільки

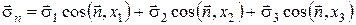
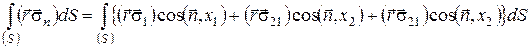
По теоремі Остроградського – Гауса:

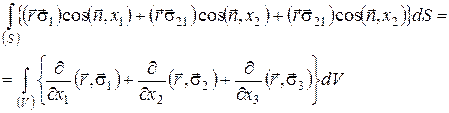
Беручи почленно похідні від векторних добутків під знаком інтеграла по об’єму, одержуємо:

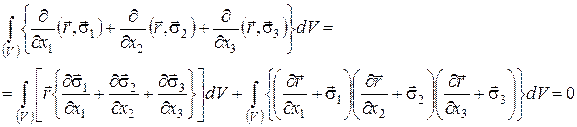(63)

Але, у силу (61), перший інтеграл у (63) обертається в нуль. Таким чином, ми приходимо до співвідношення:

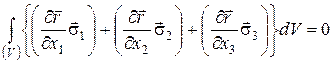(64)

Оскільки V - довільний об’єм, то дорівнює нулю підінтегральний вираз:

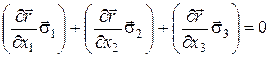
Але

; ; ; ;

; ;

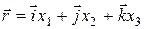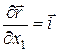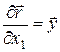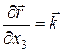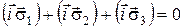
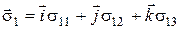
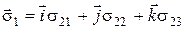
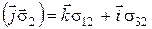
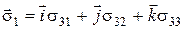
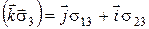
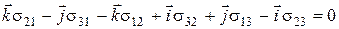
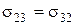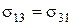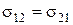
Отже, використовуючи другу умову рівноваги, ми приходимо до висновку, що тензор напружень є симетричним тензором другого рангу. У декартовій системі координат, осі якої позначені через 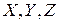, ця обставина буде виражатися рівностями:

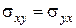
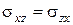(67)

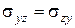
Дата добавления: 2015-05-24