Складові вектора густини електричного струму

Це збігається з виразом для закону Ома у випадку ізотропного середовища.

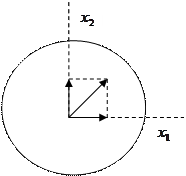Рис. 7. До аналізу матриці тензора електропровідності.

На закінчення цієї глави розглянемо коротко два моменти.

1.Коефіцієнти квадратичної форми координат являють собою компоненти симетричного тензора другого рангу.

Розглянемо рівняння , у якому 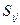є коефіцієнтами.

Докладний запис цього рівняння виглядає так:

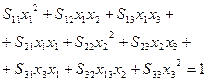(25)

Якщо припустити що, 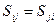, то (25) прийме вигляд:

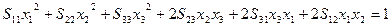
Це рівняння поверхні другого порядку, центр якого сполучений з початком координат.

Уявимо собі, що проводиться перетворення координат:

,

Тоді (25) приймає вид:

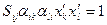(26)

З іншого боку, у новій системі координат рівняння поверхні другого порядку, центр якої збігається з початком координат, має вид:

(27)

Порівнюючи (26) і (27), одержимо:

(28)

Таким чином, дійсно коефіцієнти квадратичної форми координат компоненти тензора, що представляють собою, 2 ранги.

2. Матеріальні і польові тензори

Приклади, що ми розглянули дотепер, показують, що фізичні властивості кристалів описуються тензорами різних рангів. Тензори, що описують фізичні властивості, називаються матеріальними тензорами.

Однак, тензорами описуються не тільки фізичні властивості тіл. Ними може описуватися також стан тіла, що виник в результаті визначеного зовнішнього впливу. Наприклад, якщо до тіла прикладені зовнішні сили, тіло деформується, у ньому виникають напруги і деформації. Можна показати (це є змістом наступної глави), що для опису напруги, що виникає у суцільному пружному середовищі і деформації необхідно задати два тензори: тензор напруги і тензор деформацій. Такі тензори називаються польовими тензорами.

Матеріальні тензори, як ми бачили, визначаються симетрією даного кристала. В ізотропному середовищі властивість завжди задається одним числом.

Польові тензори визначаються не тільки будовою (у тому числі, симетрією) кристала, але і характером зовнішнього впливу, якому піддається кристал. Наприклад, напруги і деформації в пружному тілі визначаються як пружними константами самого тіла, так і тим, яку величину мають прикладені до тіла зовнішні сили, і як вони прикладені. Польові тензори далеко не завжди зводяться до одного числа навіть у цілком ізотропному тілі.

Польові і матеріальні тензори можуть бути зв'язані між собою визначеними співвідношеннями, що являють собою фізичні закони. Наприклад, два польових тензори - тензор напруги і тензор деформацій - зв'язані між собою узагальненим законом Гука, у який входять у вигляді коефіцієнтів компоненти матеріального тензора пружності.

Дата добавления: 2015-05-24