Модель циклу замовлення

У моделі циклу замовлення оптимізації підлягають такі параметри системи запасів:

- рівень максимального запасу М;

- цикл замовлення R (однаковий час між черговими поставками).

Рівень максимального запасу визначається так (2.3):

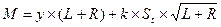. (2.3)

Беручи за основу, що річний попит має бути задоволений партіями оптимальної величини, можна розрахувати оптимальну кількість партій (закупівель) n_opt та оптимальний цикл закупівлі R_opt за такими формулами:

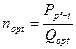; (2.4)

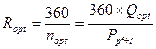. (2.5)

Отже, приймаючи на реалізацію управління запасами модель циклу замовлення, оптимальним управлінням слід уважати такий стан, коли один раз у R часу необхідно замовляти таку величину Q_і, яка б визначалася за формулою

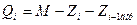, (2.6)

де Z_і – наявний запас на складі на початку і-того циклу;

Z_{і-1 дор} – можливі поставки у дорозі (для наведеного прикладу, якщо R>L ця величина дорівнює нулю).

Графічно процес використання і поповнення поточного запасу в моделі циклу замовлення можна показати на рис. 2.4.

Основними перевагами цієї моделі, порівняно з першою, є неістотні витрати моніторингу рівня запасів (один раз на початку циклу замовлення) та можливість використання норми постійної величини замовлення у разі стабільного попиту.

Запас (Z), одиниць

Максимальний розрахунковий запас

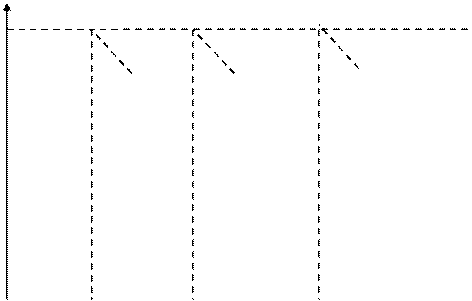
М

Q₂ M = const

Q₁ A₂ Q₃ R = const

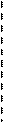
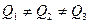
A₁ A₃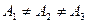

L L L Час(t), днів

R R R

Рисунок 2.4. - Графічна інтерпретація моделі циклу замовлення

Дата добавления: 2015-05-08