Вычисление распределительной способности

Трудность тестового задания

Для определения трудности тестового задания вычисляется индекс трудности по формуле

,

(2.7)

где N₁ – количество испытуемых правильно выполнивших задание; N – общее количество испытуемых. В зависимости от величины индекса трудности тестовые задания анализируют согласно табл. 2.15 [15].

Таблица 2.15

Индекс трудности тестового задания

Индекс трудности Pd	Интерпретация
Pd <= 0,20	Отгадывание правильных ответов (исключить из теста) ТЗ
0,20 < Pd<= 0,36	ТЗ слишком сложное (переформулировать задание)
0,36 < Pd<= 0,84	ТЗ средней сложности (оставить без изменения)
Pd> 0,84	ТЗ слишком легкое (исключить из теста)

В настоящее время в качестве параметра, определяющего меру трудности тестового задания, используют логит трудности тестового задания [2], который вычисляют по формуле

,

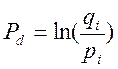(2.8),

где 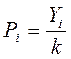– доля правильных ответов испытуемого; у_i - число правильных ответов испытуемого на к заданий; q_j – доля неправильных ответов испытуемого, определяемая по формуле q_j=1- p_j. Для оценки уровня знаний введен количественный параметр логит уровня знаний, определяемый по формуле:

.

(2.9)

Логарифмические оценки позволяют сравнивать трудность тестового задания с уровнем знания [2].

В качестве примеров анализа качества тестовых заданий в зависимости от индекса трудности рассмотрим результаты тестирования, приведенные в работе Сьюзан М. Кейс и Дэвида Б. Свенсон [15, c. 102]. Тестируемые студенты были разделены на лучшую (Hi) и худшую (Lo) группы. При небольшом количестве экзаменуемых рекомендуется включить в группу Hi 50% лучших студентов, а оставшихся в группу − Lo.

В приведенных примерах для каждого варианта ответа показан процент студентов, выбравших данный ответ в качестве правильного. Последняя строка в табл. 2.16 – 2.22 содержит проценты ответов по всей группе тестируемых. Индекс трудности рассчитывается по формуле (2.7).

Пример 1. В табл. 2.16 в группе Hi ответ А выбрали 1% студентов, ответ В – 1%, С – 94%, D – 4%, E – 1%, F – 2%. В этом же тестовом задании в группе Lo ответ А выбрали 21%, В – 6% и т.п.

Таблица 2.16

Результаты тестирования (ТЗ № 1)

Группы	A	B	C	D	E	F
Hi
Lo
Все

Для этого тестового задания Р_d = 2, индекс дискриминации – 0,05, а правильным является второй ответ.

Интерпретация тестового задания № 1: типичный пример тестового задания с некорректно выбранным правильным ответом. Если правильный ответ – В, то задание является сложным с отрицательным индексом дискриминации, а количество студентов, правильно ответивших на него, равно только 2%. Напрашивается предположение, что правильным ответом является ответ С, но в этом можно убедиться только после анализа данного тестового задания экспертом по предмету. Если правильным окажется ответ С, то Р_d = 77, а индекс дискриминации – 0,41. Оба эти значения являются исключительно хорошими с точки зрения статистики, и нет смысла изменять тестовое задание.

Пример 2. Табл. 2.17 содержит результаты тестирования по второму заданию.

Для этого тестового задания Р_d = 76, индекс дискриминации – 0,30, а правильным является третий ответ.

Интерпретация тестового задания № 2: 91% тестируемых из группы Hi и 61% из группы Lo выбрали правильный ответ. Это отличные статистические данные. Следовало бы переписать ответы 1 и 2 перед тем, как снова использовать данное тестовое задание, поскольку лишь отдельные студенты выбрали их.

Таблица 2.17

Результаты тестирования (ТЗ № 2)

Группы
Hi
Lo
Все

Пример 3. Табл. 2.18 содержит результаты тестирования по третьему заданию.

Для этого тестового задания Р_d = 34, индекс дискриминации – 0,30, а правильным является третий ответ.

Таблица 2.18

Результаты тестирования (ТЗ № 3)

Группы
Hi
Lo
Все

Интерпретация третьего тестового задания: 51% тестируемых из группы Hi и 21% из группы Lo выбрали правильный ответ. Это очень сложное тестовое задание и его необходимо переделать или заменить. Слишком много тестируемых из группы Hi выбрали вариант 1; возможно, тестовое задание плохо сформулировано. Необходимо проверить, насколько хорошо изложен ответ 1 и убедиться в том, не является ли он также правильным.

Пример 4. Табл. 2.19 содержит результаты тестирования по заданию № 4.

Таблица 2.19

Результаты тестирования (ТЗ № 4)

Группы
Hi
Lo
Все

Для этого тестового задания Р_d = 34, индекс дискриминации – 0,30, а правильным является третий ответ.

Интерпретация четвертого тестового задания: ответы на вариант 3 по группам Hi и Lo разделились, как в тестовом задании № 3, но с этим тестовым заданием может быть все в порядке. В отличие от тестового задания 3, тестируемые, не знающие правильного ответа, разделились по дистракторам, но желательно проанализировать ответы 1, 2, 4 на правильность и ясность формулировок.

Профессиональные ситуации представляют собой хороший материал для составления тестовых заданий. Одно из главных преимуществ использования профессиональных ситуаций заключается в том, что они помогают оценить применение знаний. Был проведен ряд исследований [20] для сравнения психометрических характеристик тестовых заданий, разработанных в трех форматах: задание 1-А − без использования ситуаций, задание 2-А − с использованием коротких ситуаций, задание 3-А − с использованием длинных ситуаций. Эта последовательность тестовых заданий была создана, чтобы обеспечить возрастающий уровень интерпретации, анализа и синтеза данных. Тестовые задания были включены в состав лицензионного экзамена студентам старших курсов медицинских школ США. Таблицы к заданиям указывают процентное отношение лучших (Hi) и худших (Lo) студентов (студенты, которые попали в группы с наиболее высокими и низкими результатами) (табл. 2.20 − 2.22). Почти все студенты из группы Hi (99%) и группы Lo (90%) выбрали правильный вариант ответа в формате без использования ситуации.

Задание 1-А (без использования ситуации).

Наиболее вероятная патология почек у детей с нефротическим синдромом и нормальной функцией почек – это:

a) острый постстрептококковый гломерулонефрит;

b) гемолитически-уремический синдром;

c) нефротический синдром с минимальными изменениями;

d) нефротический синдром вследствие фокального и сегментарного гломерулосклероза;

e) болезнь Шенлейна − Геноха с нефритом.

Таблица 2.20

Результаты тестирования заданий без использования ситуаций

Группы	A	B	C	D	E
Hi
Lo

Форматы с использованием коротких и длинных ситуаций не были значительно труднее для группы Hi, но явились таковыми для группы Lo: правильный ответ был выбран 82% студентов в формате с короткой ситуацией и 66% - в формате с использованием длинной ситуации.

Задание 2-А (с использованием короткой ситуации).

У двухлетнего мальчика наблюдаются отеки на протяжении недели. Артериальное давление 100/60 мм рт ст, имеются генерализованные отеки и асцит. Сывороточная концентрация креатина 0,4 мг/дл, холестерина 569 мг/дл. В анализе мочи белок 4+, кровь отсутствует. Наиболее вероятный диагноз – это (варианты ответа те же).

Таблица 2.21

Результаты тестирования с использованием короткой ситуации

Группы	A	B	C	D	E
Hi
Lo

Задание 3-А (с использованием длинной ситуации).

У чернокожего двухлетнего мальчика наблюдается отечность глаз и лодыжек на протяжении последней недели. Артериальное давление 100/60 мм рт ст, пульс 110/мин и частота дыхания 28/мин. Помимо отечности глаз и отека лодыжек, у него наблюдается увеличение живота с положительным симптомом волны. Сывороточная концентрация креатина 0,4 мг/дл, альбумина 1,4 г/дл и холестерина 569 мг/дл. В анализе мочи белок 4+, кровь отсутствует. Наиболее вероятный диагноз – это (варианта ответы те же).

Таблица 2.22

Результаты тестирования с использованием длинной ситуации

	A	B	C	D	E
Hi
Lo

тестового задания

Для оценки уровня индивидуальной подготовки студентов, позволяющей отличить сильного студента от слабого, используют коэффициент дискриминативности, принимающий значение в интервале от –1 до 1 и характеризующий распределительную способность (РС) тестового задания. Для вычисления коэффициента дискриминативности на основе результатов тестирования необходимо:

1) поделить студентов на три группы:

l слабая –25% студентов, получивших самые низкие оценки;

l средняя –50% студентов, получивших средние оценки;

l сильная –25% студентов, получивших наиболее высокие оценки;

2) для каждого тестового задания, входящего в проведенный тест, вычислить долю студентов из сильной группы, правильно ответивших на данный вопрос (Р_hi); долю студентов из слабой группы, правильно ответивших на данный вопрос (P_lo);

3) определить коэффициент дискриминативности как разность между величинами Р_hi – P_lo.

Если значение этого коэффициента равно единице, то все студенты, получившие высокие оценки за весь тест, ответили на этот вопрос правильно и ни один из студентов, получивших низкие оценки за весь тест, не ответил на вопрос правильно. В этом случае можно почти со стопроцентной гарантией отличить сильного студента от слабого.

Отрицательные значения коэффициента дискриминативности обусловлены ошибочным указанием в тестовом задании неверного ответа, некорректной формулировкой задания.

Близкие к нулю (но положительные) значения коэффициента дискриминативности (0…0.3) могут быть обусловлены чрезмерной трудностью тестового задания, на которое не могут ответить ни «сильные», ни «слабые» студенты, или легкостью тестового задания, на которое могут ответить и «сильные», и «слабые» студенты. Такие тестовые задания необходимо исключить из теста или модифицировать тестовое задание (изменить формулировку или ответы).

По результатам первичного тестирования можно построить график распределения частот «сырых» баллов. Гипотетические графики распределения частот показаны на рис. 2.2.

Степень отклонения графика распределения частот измеряемого признака от симметричного вида относительно среднего значения называется асимметрией (As) (рис. 2.2).

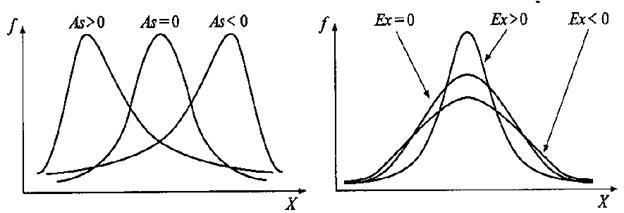
Рис. 2.2 Распределение частот «сырых» баллов

Мерой плосковершинности или остроконечности графика распределения частот измеряемого признака является эксцесс (Ех)

(рис 2.2).

В зависимости от значения, знака асимметрии (As) и эксцесса (Ex) результаты тестирования можно сгруппировать в девять групп, которые определяют критерии качественного анализа теста. Интерпретировать значения асимметрии и эксцесса можно по табл. 2.23.

Таблица 2.23

Интерпретация значений асимметрии и эксцесса

Группа	Асимметрия (As)	Эксцесс (Ex)	Интерпретация текста
	As = 0	Ex = 0	Валидный
	As < 0	Ex > 0	Легкий, малая распределительная способность
	As < 0	Ex < 0	Легкий, большая распределительная способность
	As < 0	Ex = 0	Легкий
	As > 0	Ex < 0	Сложный, большая распределительная способность
	As > 0	Ex > 0	Сложный, малая распределительная способность
	As > 0	Ex = 0	Сложный
	As = 0	Ex > 0	Неоднородный, малая распределительная способность
	As = 0	Ex < 0	Неоднородный, большая распределительная способность

Дата добавления: 2015-05-24