Лабораторна робота №5. Тема: Дослідження технологій виконання матричних операцій в Excel

Тема: Дослідження технологій виконання матричних
операцій в Excel

Мета: Навчитися виконувати математичні операції з матрицями засобами програми Excel.

Час виконання: 4 години.

Навчальні питання:

1. Додавання та множення матриць.

2. Транспонування матриць.

3. Обернення матриць.

4. Обчислення детермінанту.

Завдання та методичні рекомендації:

– додавання двох матриць та множення матриці на скаляр виконують за допомогою звичайних формул або формул масивів;

– добуток матриць, транспонування та обернення матриць виконуються як функції (формули) масивів.

1. Виконати додавання матриць двома способами: звичайними формулами (використати автозаповнення) та формулами масивів (А + В).

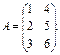
1)	2)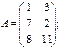

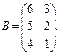
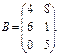
2. Помножити матрицю на скаляр.

МР: використати абсолютні посилання $А$I у формулі та автозаповнення.

1) 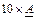;	2) ;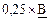

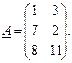
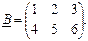
3. Знайти добуток двох матриць.

МР: кількість стовпчиків першої матриці повинна дорівнювати кількості рядків другої матриці; внутрішні розміри збігаються;

для результату виділити діапазон, який визначається кількістю рядків першої матриці і кількістю стовпчиків другої, тобто розміри результуючої матриці складаються із „зовнішніх” розмірів;

функція МУМНОЖ (матриця 1; матриця 2);

завершення операції: <ctrl + shift + Enter>.

1) , , ;

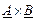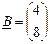2) , , .

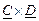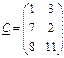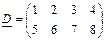4. Транспонування матриць двома способами.

МР: спосіб 1: копіювання через буфер обміну за допомогою команди Специальная вставка в меню Правка або контекстному меню;

спосіб 2: функція ТРАНСП (матриця) – для даного способу необхідно виділити діапазон відповідного (транспонованого) розміру і завершити операцію: <ctrl + shift + Enter>.

; ;

; .

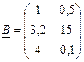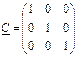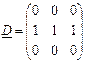5. Обчислення детермінанта матриці.

МР: обчислюється тільки для квадратних матриць;

якщо детермінант det A = 0, тоді матриця – сингулярна (особова) і обернення матриці виконати неможливо;

якщо det A 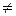0, тоді матриця – несингулярна (не особова), її можна обертати;

функція МОПРЕД (матриця).

Обчислити det A:

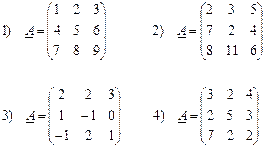
6. Обернення матриць.

МР: det A 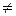0, тобто матриця повинна бути несингулярною;

виділити діапазон для результату, який відповідає початковій матриці;

функція МОБР (матриця);

завершення операції: <ctrl + shift + Enter>.

Виконати обчислення матриць 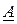попереднього завдання.

7. Розв’язування систем лінійних рівнянь.

МР: нехай дано систему рівнянь .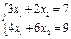

Запишемо її у матричній формі

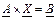, тоді ,

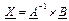де 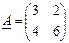; ; 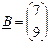; 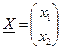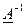– матриця, обернена до матриці .

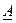Для того щоб знайти корені системи треба обернути матрицю 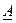та виконати множення матриць .

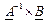Розв’язати системи рівнянь, для яких існують рішення:

; ;

; ;

.

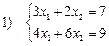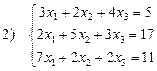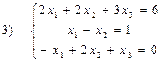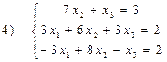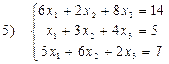Дата добавления: 2015-05-24