
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Обратная матрица
|
|
|
|
Обратная матрица существует только тогда,когда еее определитель не равен нулю. Матрица 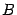 называется обратной матрицей для квадратной матрицы
называется обратной матрицей для квадратной матрицы  , если
, если 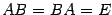 . Из определения следует, что обратная матрица
. Из определения следует, что обратная матрица 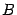 будет квадратной матрицей того же порядка, что и матрица
будет квадратной матрицей того же порядка, что и матрица  (иначе одно из произведений
(иначе одно из произведений 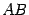 или
или  было бы не определено). Обратная матрица для матрицы
было бы не определено). Обратная матрица для матрицы  обозначается
обозначается  . Таким образом, если
. Таким образом, если  существует, то
существует, то 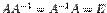 . Из определения обратной матрицы следует, что матрица
. Из определения обратной матрицы следует, что матрица  является обратной для матрицы
является обратной для матрицы  , то есть
, то есть  . Про матрицы
. Про матрицы  и
и  можно говорить, что они обратны друг другу или взаимно обратны. Предложение 14. 20 Если матрица
можно говорить, что они обратны друг другу или взаимно обратны. Предложение 14. 20 Если матрица  имеет обратную, то
имеет обратную, то 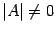 и
и 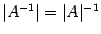 . Доказательство. Так как определитель произведения матриц равен произведению определителей,то
. Доказательство. Так как определитель произведения матриц равен произведению определителей,то  . По следствию
. По следствию 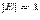 , поэтому,
, поэтому, 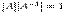 что невозможно при
что невозможно при 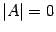 . Из предыдущего равенства следует также
. Из предыдущего равенства следует также 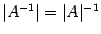 . Последнее предложение можно сформулировать в следующем виде. Если определитель матрицы равен нулю, то обратная к ней не существует. Так как для нахождения обратной матрицы важно, равен ли определитель марицы нулю или нет, то введем следующие определения. Определение 14. 9 Квадратную матрицу
. Последнее предложение можно сформулировать в следующем виде. Если определитель матрицы равен нулю, то обратная к ней не существует. Так как для нахождения обратной матрицы важно, равен ли определитель марицы нулю или нет, то введем следующие определения. Определение 14. 9 Квадратную матрицу  назовем вырожденной или особенной матрицей, если
назовем вырожденной или особенной матрицей, если 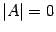 , и невырожденной или неособенной матрицей, если
, и невырожденной или неособенной матрицей, если 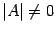 . Предложение 14. 21 Если обратная матрица существует, то она единственна. Доказательство. Пусть две матрицы
. Предложение 14. 21 Если обратная матрица существует, то она единственна. Доказательство. Пусть две матрицы 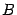 и
и 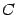 являются обратными для матрицы
являются обратными для матрицы  . Тогда
. Тогда 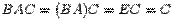 и
и  Следовательно,
Следовательно,  . Предложение 14. 22 Если квадратная матрица
. Предложение 14. 22 Если квадратная матрица  является невырожденной, то обратная для нее существует и
является невырожденной, то обратная для нее существует и 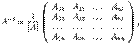 где
где  -- алгебраические дополнения к элементам
-- алгебраические дополнения к элементам 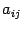 . Доказательство. Так как для невырожденной матрицы
. Доказательство. Так как для невырожденной матрицы  правая часть равенства (14.14) всегда существует, то достаточно показать, что эта правая часть является обратной матрицей для матрицы
правая часть равенства (14.14) всегда существует, то достаточно показать, что эта правая часть является обратной матрицей для матрицы  . Обозначим правую часть равенства (14.14) буквой
. Обозначим правую часть равенства (14.14) буквой 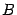 . Тогда нужно проверить, что
. Тогда нужно проверить, что 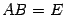 и что
и что 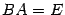 . Докажем первое из этих равенств, второе доказывается аналогично. Пусть
. Докажем первое из этих равенств, второе доказывается аналогично. Пусть  . Найдем элементы матрицы
. Найдем элементы матрицы 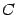 , учитывая, что
, учитывая, что  :
:  Если
Если 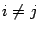 , то по предложению 14.17 сумма справа равна нулю, то есть
, то по предложению 14.17 сумма справа равна нулю, то есть 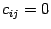 при
при 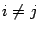 . Если
. Если  , то
, то  Сумма справа представляет собой разложение определителя матрицы
Сумма справа представляет собой разложение определителя матрицы  по
по  -ой строке (предложение 14.16). Таким образом,
-ой строке (предложение 14.16). Таким образом,  Итак, в матрице
Итак, в матрице 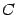 диагональные элементы равны 1, а остальные равны нулю, то есть
диагональные элементы равны 1, а остальные равны нулю, то есть  . Результаты предложений 14.20, 14.21, 14.22 соберем в одну теорему. Замечание.Следует обратить особое внимание на места, занимаемые алгебраическими дополнениями в формуле обратной матрицы: первый индекс показывает номер столбца, а второй -- номер строки, в которые нужно записать вычисленное алгебраическое дополнение.
. Результаты предложений 14.20, 14.21, 14.22 соберем в одну теорему. Замечание.Следует обратить особое внимание на места, занимаемые алгебраическими дополнениями в формуле обратной матрицы: первый индекс показывает номер столбца, а второй -- номер строки, в которые нужно записать вычисленное алгебраическое дополнение.
|
|
|
|
|
Дата добавления: 2015-05-08; Просмотров: 381; Нарушение авторских прав?; Мы поможем в написании вашей работы!