
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Логические отношения между сложными суждениями
При решении данной задачи необходимо учитывать, что – логический термин – знак отрицания.
Пример: a 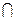 b
b 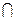 c – Я работаю в офисе, и я люблю свою профессию,
c – Я работаю в офисе, и я люблю свою профессию,
и я учусь в университете.
Упражнение 12
Установите, являются ли данные формулы тождественно - истинными (или логическими законами).
1. a → (a 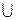 b);
b);
2. b → (a 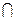 b);
b);
3. (a → b) → (b → a);
4. a 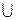 b
b 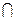
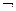 a;
a;
5. (a 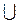 b) → b;
b) → b;
6. (a → b) → (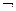 b →
b → 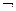 a).
a).
7. ((a → b) 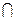 a)→ b.
a)→ b.
8. ((a → b) 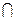
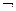 b) →
b) → 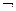 a.
a.
9. a 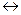 a.
a.
10. ((a 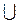 b)
b) 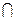 a) →
a) → 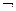 b.
b.
Пример: (а ∩ b) 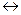 (b ∩ a) – является логическим законом
(b ∩ a) – является логическим законом
| a | b | a∩b | b∩a | (а ∩ b) 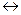 (b ∩ a) (b ∩ a)
|
| и | и | и | и | и |
| и | л | л | л | и |
| л | и | л | л | и |
| л | л | л | л | и |
Сложные суждения могут быть сравнимыми и несравнимыми.
Несравнимые – это суждения, которые не имеют общих составляющих (пропозициональных) переменных. Например, р ∩ g и m ∩ n.
Сравнимые – это суждения, которые имеют одинаковые составляющие (пропозициональные) переменные и различаются логическими связками, включая отрицание. Например, сравнимыми являются следующие два суждения: «Украина или Болгария имеют выход в Черное море» (р U g); «Ни Украина, ни Болгария не имеют выхода в черное море» (┐р ∩ ┐g).
Сложные сравнимые суждения могут быть совместимыми и несовместимыми.
Совместимыми являются такие сравнимые суждения, которые одновременно могут быть истинными. Различают три вида совместимости сложных суждений: эквивалентности; частичная совместимость и подчинение.
Эквивалентные – это суждения, которые принимают одни и те значения, т. е. одновременно являются либо истинными, либо ложными.
Отношение эквивалентности позволяет выражать одни сложные суждения через другие – конъюнкцию через дизъюнкцию или импликацию, и наоборот.
- выражение конъюнкции через дизъюнкцию: ┐ (а ∩ b) ↔ ┐a U ┐b.
- выражение дизъюнкции через конъюнкцию: ┐(а U b) ↔ ┐a ∩ ┐b.
- выражение импликации через конъюнкцию: ┐(a → b) ↔ (a ∩ ┐b).
- выражение импликации через дизъюнкцию: а → b ↔ ┐a U b.
Частичная совместимость характерна для суждений, которые могут быть одновременно истинными, но не могут быть одновременно ложными.
Подчинение между суждениями имеет место в том случае, когда при истинности подчиняющего подчиненное всегда будет истинным.
Отношение логического подчинения, позволяющее по истинности подчиняющего суждения определить истинность подчиненного, составляет основу фундаментального в науке логики понятия логического следования, регулирующего все виды рассуждений.
Несовместимыми являются суждения, которые одновременно не могут быть истинными. Из двух видов несовместимости одна – противоположность, другая противоречие.
Противоположность – отношение между суждениями, которые одновременно не могут быть истинными, но могут быть одновременно ложными, при ложности одного из противоположных суждений нельзя установить значение другого: оно может быть как истинным, так и ложным.
Противоречие – отношение между суждениями, которые одновременно не могут быть ни истинными, ни ложными. При истинности одного из них другое будет ложным, а при ложности первого второе будет истинным.
Чтобы получить сложное суждение, противоречащее исходному, последнее нужно подвергнуть отрицанию. Например, для g противоречащим будет ┐g; для конъюнкции р ∩ g противоречием будет ее отрицание - ┐(р ∩ g).
|
|
Дата добавления: 2015-05-08; Просмотров: 970; Нарушение авторских прав?; Мы поможем в написании вашей работы!