Порядок выполнения работы

Цель работы

Исследование передаточных функций, переходных и частотных характеристик динамических звеньев линейных систем автоматического управления

Целью работы является изучение типовых звеньев линейных систем автоматического управления, приобретение и закрепление навыков моделирования элементов систем в программе Vissim и MathCAD, исследование их переходных и частотных характеристик.

1.2 Методичні вказівки з організації самостійної роботи студентів

Типовые звенья линейных систем можно определять различными эквивалентными способами, в частности с помощью, так называемой передаточной функции, имеющей, как правило, дробно-рациональный вид, т.е. представляющей собой отношение двух полиномов:

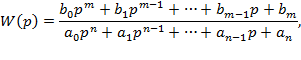
где b_i и a_j – коэффициенты полиномов.

Передаточная функция связывает изображение Y(p) выходного сигнала y(t) звена с изображением X(p) его входного сигнала x(t):

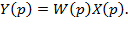
т.е. позволяет по любому известному входному сигналу x(t) найти выходной y(t). Это значит что с точки зрения ТАУ передаточная функция полностью характеризует систему управления или ее звено. Это же самое можно сказать и в отношении совокупности коэффициентов полиномов числителя и знаменателя передаточной функции.

Исследуемые звенья:

- пропорциональное звено это звено, выходной сигнал которого пропорционален входному:

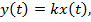
где к - коэффициент усиления;

передаточная функция равна:

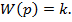
- идеально-интегрирующее звено это звено, выходной сигнал которого пропорционален интегралу по времени от входного:

передаточная функция равна:

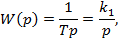
где T [сек] – постоянная времени интегратора,

k₁ = 1/Т [1/сек] - коэффициент усиления интегратора

- апериодическое звено 1-го порядка это звено, выходной сигнал y(t) которого связан с входным х(t) дифференциальным уравнением

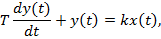
передаточная функция равна:

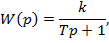
где k – коэффициент усиления (размерный или безразмерный) и T – постоянная времени, сек.

- колебательное, апериодическое 2-го порядка, консервативное звенья это звенья, выходной сигнал y(t) которого связан со входным сигналом x(t) дифференциальным уравнением:

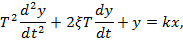
где k – коэффициент усиления, T – постоянная времени и декремент затухания .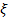

В зависимости от значения 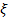разделяют передаточные функции:

- апериодического звена 2-го порядка

- колебательного звена

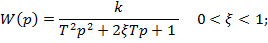
- консервативного звена

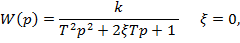
Переходная функция h(t) это реакция, отклик линейной системы или звена на ступенчатое единичное воздействие 1(t) (рисунок 1.1).

Переходная функция это своеобразный «отпечаток пальца» звена – каждое звено имеет свою особенную, отличающуюся от переходных функций других звеньев, переходную функцию, по которой можно определить тип и параметры звена.

Переходная функция модели САР позволяет характеризовать ее качество (быстродействие и точность) в переходном режиме работы. Кроме того, зная переходную функцию линейной системы можно определить реакцию системы на произвольное воздействие.

Важное для практики приложение переходной функции – идентификация объектов и систем: определение по экспериментально снятой переходной функции вида типового звена, которым можно промоделировать отдельные элементы и системы в целом, а также возможность определения параметров моделирующих звеньев.

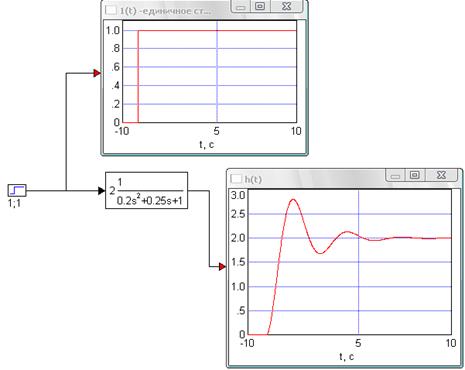
Рисунок 1.1 - Пример виртуального лабораторного стенда, построенного в программе Vissim, для определения переходных характеристик звеньев, и осциллограмма переходной функции колебательного звена. Его переходная функция колебательно стремится к значению 2.

Задание к работе

Определить влияние параметров типовых звеньев на переходные и частотные характеристики.

1.Переходные характеристики

Построить в программе Vissim виртуальный лабораторный стенд для исследования моделей звеньев (рисунок 1.2).

Аналогично получить стенды для исследования остальных типовых звеньев.

Установить связь параметров звеньев с параметрами его переходной функции.

Определить параметры звеньев по их переходным функциям, сравнить с заданными на стенде значениями.

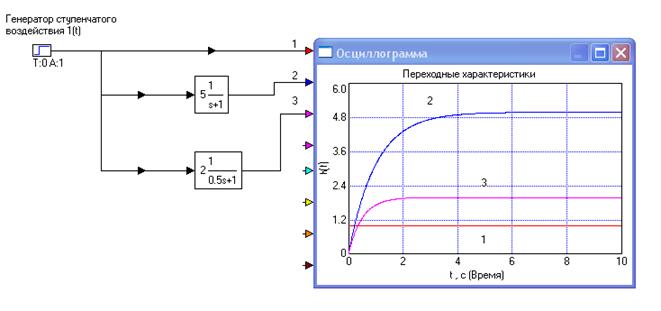
Рисунок 1.2 – Стенд для исследования апериодического звена 1-го порядка

Изменить параметры звеньев и запустив моделирование проверить, к каким изменениям переходных функций это привело.

Как определить постоянную времени интегратора по его переходной функции?

Как определить коэффициент усиления колебательного звена по его переходной функции?

Сделать выводы, занести их в отчет вместе со снимком экрана лабораторного стенда.

2. Частотные характеристики

Построить в программе Vissim виртуальный лабораторный стенд и получить частотные характеристики для всех исследуемых звеньев (рисунок 1.3).

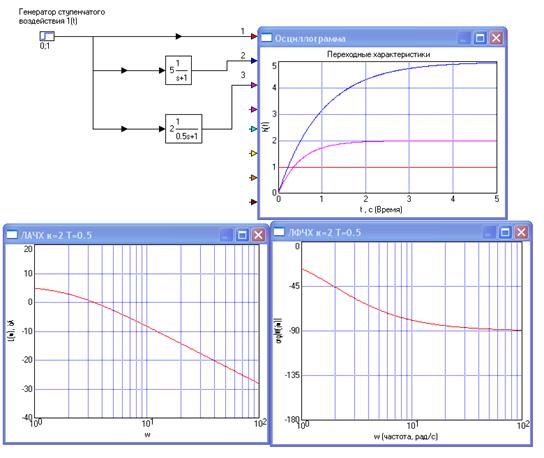
Рисунок 1.3 – Стенд для исследования частотных характеристик апериодического звена 1-го порядка

1. Запустить Vissim. Установить кириллицу: View (Вид) - Fonts (Шрифты) - выбрать шрифт MS Sans Serif, кириллица, размер 8).

2. Выбрать красивое оформление блоков и линий связи: View (Вид) - Presentation Mode (Режим презентации).

3. Построить в программе Vissim виртуальный лабораторный стенд для исследования, например, модели апериодического звена.

Вынести на рабочее поле Vissim’а генератор step ступенчатого сигнала (Blocks – Signal Producer - step), и осциллограф (Blocks – Signal Consumer – Plot), сделать надписи (Blocks – Annotation - lebel)

Апериодическое звено создается вынесением на рабочее поле блока transferFunction (Blocks – Linear System - transferFunction) и заданием его параметров.

Параметры апериодического звена задаются в окне диалога, появляющегося при двойным щелчке по блоку transferFunction:

Числитель передаточной функции

Знаменатель передаточной функции

Коэфициент усиления

Рисунок 1.4 - Поля окна диалога для задания параметров звена

Пояснения по настройке виртуального лабораторного стенда (заданию параметров моделирования).

- Для отображения под блоками, в частности под блоком генератора ступенчатой функции (step), их параметров следует выбрать в меню View пункт Block Labels (Подписи Блоков).

- время моделирования Rng выбрано (Simulate – Simulation Properties – вкладка Range: Start и End) изменяющимся от -1 сек до 5 сек. Это сделано для повышения наглядности сциллограммы, чтобы показать часть оси времени левее нуля и поведение там исследуемых функций;

- шаг моделирования Step (там же Step Size) выбран равным 0.001 сек;

- Т – текущее время, параметр, полезный при моделировании в реальном времени (Simulate – Simulation Properties - вкладка Range: отметить при необходимости Run In Real Time);

- RK2 – интегрирование проводится по методу Рунге-Кутты 2 порядка.

Сохранить лабораторный стенд с содержательным названием в личной папке.

4. Определить по осциллограммам постоянные времени и коэффициенты усиления звеньев и указать, какая кривая соответствует какому звену.

Дата добавления: 2015-05-09