Коэффициент напряженности

Величина полного резерва времени далеко не всегда может достаточно точно характеризовать, насколько напряженным является выполнение той или иной работы некритического пути. Все зависит от того, на какую продолжительность работ распространяется вычисленный резерв, какова продолжительность этой последовательности. Определить степень трудности выполнения в срок каждой группы работ некритического пути можно с помощью коэффициента напряженности работ.

Коэффициентом напряженности К_н работы (i,j) называется отношение продолжительности несовпадающих (заключенных между одними и теми же событиями) отрезков пути, одним из которых является путь максимальной продолжительности, проходящий через данную работу, а другим – критический путь:

,

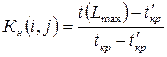где – продолжительность максимального пути, проходящего через работу (i,j);

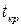– продолжительность (длина) критического пути;

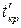– продолжительность отрезка рассматриваемого пути, совпадающего с критическим путем.

Данную формулу можно привести к виду:

,

где 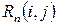– полный резерв времени работы (i,j).

Ø Важно помнить. Коэффициент напряженности может изменяться в пределах от 0 до 1.

Коэффициент напряженности равен 0 для работ, у которых отрезки максимального из путей, не совпадающие с критическим путем, состоят из фиктивных работ нулевой продолжительности, и равен 1 для работ критического пути.

Пример решения задачи. Для заданного ранее сетевого графика найти коэффициент напряженности работы (1,4) и работы (3,5).

Так как работа (3,5) лежит на критическом пути, то ее коэффициент напряженности равен 1: .

Коэффициент напряженности работы (1,4) вычислим двумя способами.

Ранее было установлено, что продолжительность критического пути равна 61 суткам. А максимальный путь, проходящий через работу (1,4), имеет следующую топологию: и продолжительность 49 суток. Этот путь совпадает с критическим на отрезке , продолжительность которого 32 суток. Подставляя эти значения в формулу, получим:

.

По другой формуле полный резерв работы (1,4) равен , следовательно

.

То есть в обоих случаях результат, естественно, получился одинаковым.

Задание для самостоятельной работы.

Для заданного сетевого графика найти:

• параметры событий (ранний срок свершения, поздний срок свершения и резерв времени);

• параметры работ (ранний срок начала работы, поздний срок начала работы, ранний срок окончания работы и полный резерв времени);

• вероятность того, что проект будет выполнен в срок, равный 27 суткам ;

• максимальный срок выполнения проекта с вероятностью 0,9;

• коэффициент напряженности работы (4,5) и работы (3,7).

Дано, что .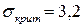

Рис. 3.3. Сетевой график

Оптимизация сетевого графика представляет процесс улучшенияорганизации выполнения комплекса работ с учетом срока его выполнения. Оптимизация проводится с целью сокращения длины критического пути, выравнивания коэффициентов напряженности работ, рационального использования ресурсов.

В первую очередь принимаются меры по сокращению продолжи­тельности работ, находящихся на критическом пути. Это достигается:

• перераспределением всех видов ресурсов, как временных (использование резервов времени некритических путей), так и трудовых, материальных, энергетических (например, перевод части исполнителей, оборудования с некритических путей на работы критического пути); при этом перераспределение ресурсов должно идти, как правило, из зон, менее напряженных, в зоны, объединяющие наиболее напряженные работы;

• сокращением трудоемкости критических работ за счет передачи части работ на другие пути, имеющие резервы времени;

• параллельным выполнением работ критического пути; пересмотром топологии сети, изменением состава работ и структуры сети.

В процессе сокращения продолжительности работ критический путь может измениться. В дальнейшем процесс оптимизации будет направлен на сокращение продолжительности работ нового критического пути, и так будет продолжаться до получения удовлетворительного результата. В идеале длина любого из полных путей может стать равной длине критического пути или, по крайней мере, пути критической зоны. Тогда все работы будут вестись с равным напряжением, а срок завершения проекта существенно сократится.

Весьма эффективным является использование метода стати­стического моделирования, основанного на многократных последо­вательных изменениях продолжительности работ (в заданных пределах) и "проигрывании" на компьютере различных вариантов сетевого графика с расчетами всех его временных параметров и коэффициентов напряженности работ. Процесс «проигрывания» продолжается до тех пор, пока не будет получен приемлемый вариант плана или пока не будет установлено, что все имеющиеся возможности улучшения плана исчерпаны и поставленные перед разработчиком проекта условия невыполнимы.

На практике при попытках эффективного улучшения составленного плана неизбежно введение дополнительно к оценкам сроков фак­тора стоимости работ.

Оптимизация сетевого графика в зависимости от полноты ре­шаемых задач может быть условно разделена на частную и ком­плексную. Видами частной оптимизациисетевого графика явля­ются: минимизация времени выполнения комплекса работ при заданной его стоимости; минимизация стоимости комплекса работ при заданном времени выполнения проекта. Комплексная оптимизацияпредставляет собой нахождение оптимального соотношения величин стоимости и сроков выполнения проекта в зависимости от конкретных целей, ставящихся при его реализации.

При линейной зависимости стоимости работ от их продолжительности задача построения оптимально сетевого графика может быть сформулирована как задача линейного программирования, в которой необходимо минимизировать стоимость выполнения проекта при двух группах ограничений. Первая группа ограничений показывает, что продолжительность каждой работы должна находиться в указанных пределах. Вторая группа ограничений требует, чтобы продолжительность любого полного пути сетевого графика не превышала установленного директивного срока выполнения проекта.

Задание для самостоятельной работы.

Фирма может влиять дополнительным финансированием на скорость строительства своего торгового павильона. Очередность выполнения работ, их нормальная и ускоренная продолжительность выполнения, а также стоимость строительно-монтажных работ при нормальном и ускоренном режиме их выполнения приведены в следующей таблице.

Таблица 3.3

Условие задачи

Имя работы	a	b	c	d	e	f	g	h	k	l
Опирается на работу	C,G	E, F		A,H	A,H	C,G	L		L
Нормальный срок (дни)
Ускоренный срок (дни)
Нормальная стоимость (тыс. руб.)
Плата за ускорение (тыс. руб.)

Требуется:

1. С учетом технологической последовательности работ построить сетевой график выполнения этих работ.

2. Рассчитать временные характеристики сетевого графика при нормальном режиме выполнения работ.

3. Найти все критические пути и их продолжительность, определить стоимость всего комплекса работ.

4. Указать стратегию минимального удорожания комплекса работ при сокращении сроков строительства на 4 дня. В какую итоговую сумму обойдется фирме ускоренная стройка павильона?

Что означают следующие термины и понятия?

Граф	Полный путь
Вершины	Критический путь
Ребра	Ранний срок свершения события
Гамильтоновый граф	Поздний срок свершения события
Эйлеговый граф	Резерв времени события
Дерево	Ранний срок начала работы
Сетевая модель	Поздний срок начала работы
Событие	Ранний срок окончания работы
Исходное событие	Поздний срок окончания работы
Завершающее событие	Резерв времени работы
Действительная работа	Резерв времени пути
Ожидание	Коэффициент напряженности работы
Фиктивная работа	Частная оптимизация
Путь	Комплексная оптимизация

Теперь вы должны уметь:

o с учетом технологической последовательности работ строить сетевой график выполнения этих работ;

o рассчитывать временные характеристики сетевого графика (событий и работ);

o находить критические пути и их продолжительность;

o определять стратегию минимального удорожания комплекса работ при сокращении сроков;

o определять коэффициенты напряженности работ;

o оценивать вероятность того, что срок выполнения проекта t_кр не превзойдет заданного директивного срока Т;

o определять максимальный срок выполнения проекта Т, который возможен с заданной надежностью (вероятностью) β.

Контрольные вопросы:

1. Основные элементы сетевой модели.

2. Правила построения сетевых графиков.

3. Понятие ранга события.

4. Временные параметры событий.

5. Временные параметры работ.

6. Сетевое планирование в условиях неопределенности.

7. Коэффициент напряженности работы: что показывает и как определяется?

8. В чем суть оптимизации сетевого графика?

Дата добавления: 2015-05-09