Системы массового обслуживания с отказами

В системах с отказами заявка, поступившая в момент, когда все каналы обслуживания заняты, немедленно получает отказ, покидает систему и в дальнейшем в процессе обслуживания не участвует.

Имеется n каналов в обслуживании, на которые поступает поток заявок с интенсивностью λ. Поток обслуживания имеет интенсивность μ (величина, обратная среднему времени обслуживания ). Требуется найти вероятности состояний СМО и характеристики ее эффективности.

Так как оба потока – заявок и освобождений – простейшие, процесс, протекающий в системе, будет марковским. Рассмотрим ее как систему с конечным множеством состояний:

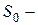свободны все каналы;

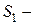занят ровно один канал;

…

заняты k каналов;

…

заняты все n каналов/

Через 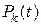обозначим вероятность того, что в момент времени t система будет находиться в состоянии .

Простейшие задачи для систем массового обслуживания с отказами были впервые решены А.К. Эрлангом. Им же были выведены формулы оценки функционирования этих систем при условии поступления простейшего потока заявок и для показательного закона распределения времени обслуживания.

Для установившегося процесса обслуживания при этих условиях Эрланг получил следующие зависимости.

· Вероятность того, что обслуживанием заняты k аппаратов (линий, приборов и т.п.):

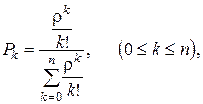(4.1)

где 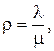k – количество занятых аппаратов,

λ – интенсивность потока заявок,

μ – интенсивность потока обслуживания.

Частные случаи:

· Вероятность простоя ( того, что все обслуживающие аппараты свободны, нет заявок):

(4.2)

· Вероятность отказа (вероятность того, что все обслуживающие приборы заняты):

(4.3)

Отсюда находим относительную пропускную способность, т.е. среднюю долю пришедших заявок, обслуживаемых системой, – вероятность того, что заявка будет обслужена:

(4.4)

Абсолютную пропускную способность, т.е. среднее число заявок, обслуживаемых в единицу времени, получим, умножив интенсивность потока заявок на относительную пропускную способность:

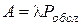
Абсолютная пропускная способность – это интенсивность потока обслуженных системой заявок, а каждый занятый канал в единицу времени обслуживает в среднем μ заявок. Значит, среднее число занятых каналов равно

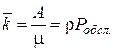(4.5)

Доля каналов, занятых обслуживанием (коэффициент загрузки):

(4.6)

Пример решения задачи.

На вход трехканальной СМО с отказами поступает поток заявок с интенсивностью λ = 4 заявки в минуту. Время обслуживания заявки одним каналом 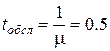мин.

Найти показатели эффективности работы системы.

Решение.

Находим вероятность простоя трехканальной СМО по формуле (4.2):

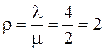- загрузка системы (среднее число заявок, приходящих за среднее время обслуживания одной заявки).

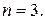
Вероятность отказа определяем по формуле (4.3):

Относительная пропускная способность системы:

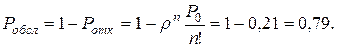
Абсолютная пропускная способность системы (среднее число заявок, обслуживаемых в единицу времени):

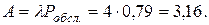
Среднее число занятых каналов (в ед. времени) определяем по формуле (4.5):

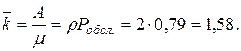
Доля каналов, занятых обслуживанием (формула (4.6)):

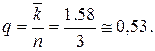
Среднее время пребывания заявки в СМО находим как вероятность того, что заявка принимается к обслуживанию, умноженную на среднее время обслуживания:

мин.

Дата добавления: 2015-05-09