С ожиданием и ограниченной длинной очереди

Системы массового обслуживания

Имеется n -канальная СМО с ожиданием, в которой количество заявок, стоящих в очереди, ограничено числом m, т.е. заявка, заставшая все каналы занятыми, становится в очередь, только если в ней находится менее m заявок.

Если число заявок в очереди равно m, то последняя прибывшая заявка в очередь не становится и покидает систему необслуженной.

Системы с ограниченной очередью являются обобщением двух рассмотренных ранее СМО: при m = 0 получаем СМО с отказами, при m = ¥ получаем СМО с ожиданием.

· Вероятность простоя ( того, что все обслуживающие аппараты свободны, нет заявок):

(4.18)

· Вероятность отказа в обслуживании равна вероятности 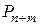того, что в очереди уже стоят m заявок:

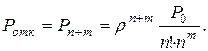(4.19)

· Относительная пропускная способность есть величина, дополняющая вероятность отказа до 1, т.е. вероятность обслуживания:

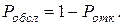
(4.20)

· Абсолютная пропускная способность определяется равенством:

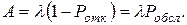(4.21)

· Среднее число занятых обслуживанием каналов:

(4.22)

· Среднее число заявок в очереди (средняя длина очереди)

(4.23)

· Среднее время ожидания обслуживания в очереди

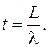(4.24)

· Среднее число заявок в системе

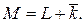(4.25)

· Среднее время пребывания заявки в системе

(4.26)

Пример решения задачи.

В парикмахерской работают 3 мастера, в зале ожидания расположено 3 стула. Поток клиентов имеет интенсивность λ = 12 клиентов в час. Среднее время обслуживания заявки мин. Определить относительную и абсолютную пропускную способность системы, среднее число занятых кресел, среднюю длину очереди, среднее время, которое клиент проводит в парикмахерской.

Решение

Для данной задачи

Определяем вероятность простоя по формуле (4.18):

Вероятность отказа в обслуживании определим по формуле (4.19)

Относительная пропускная способность, т.е. вероятность обслуживания:

Абсолютная пропускная способность (среднее число заявок, обслуживаемых в единицу времени):

Среднее число занятых обслуживанием каналов (парикмахеров):

Среднее число заявок в очереди (средняя длина очереди)

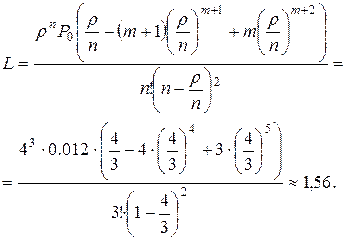
Среднее время ожидания обслуживания в очереди

ч.

Среднее число заявок в системе

.

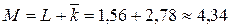Среднее время пребывания заявки в системе

ч.

Дата добавления: 2015-05-09