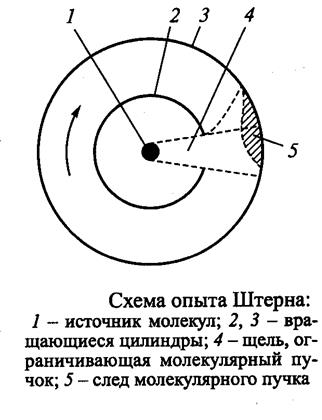
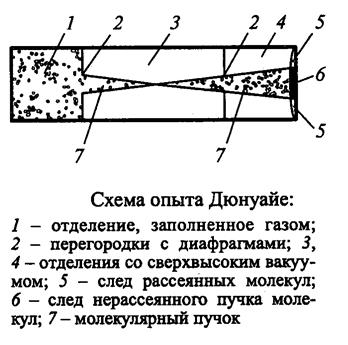
Экспериментальное подтверждение молекулярно-кинетической теории

.

Таким образом сила, действующая на участок Δ S в соответствии с основным уравнением динамики равна:

.

Давление на стенку сосуда .

Так как все направления для векторов скоростей молекул равновероятны, то средние значения квадратов модулей их проекций на координатные оси равны между собой:

т.е. и

.

Учитывая, что на самом деле, молекулы движутся с разными скоростями, необходимо вместо квадрата скорости поставить среднее значение квадрата скорости всех молекул:

.

Окончательно получаем уравнение Клаузиуса или основное уравнение МКТ:

.

Выразив плотность вещества через т ₀ и п

,

получим ещё одно выражение для основного уравнение МКТ

.

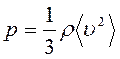Величина есть средняя кинетическая энергияпоступательного движения молекул, а величину

называют средней квадратичной скоростью молекул.

Сравнивая основное уравнение МКТ с уравнением состояния идеального газа

p = n ^. k ^. T,

получаем и .

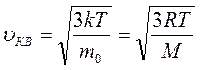Таким образом, можно утверждать, что температура макросистемы хоть и измеряется с помощью макроскопического прибора – термометра и является макроскопическим параметром, она имеет в МКТ смысл микроскопического параметра, а, именно, термодинамическая температура является величиной прямо пропорциональной кинетической энергии теплового движения молекул.

В молекулярной физике энергию теплового движения можно выражать и в кельвинах и в джоулях:

1 К = 1,38 ^. 10^–23 Дж

1 Дж = 7,246 ^. 10²² К.

Наряду с поступательным движением возможно также вращение молекулы и колебания атомов, входящих в состав молекулы.

Числом степеней свободы называют число независимых координат, определяющих положение системы (в нашем случае – молекулы). Для определения положения центра масс молекулы необходимо задать три координаты. Это означает, что молекула имеет три поступательных степени свободы.

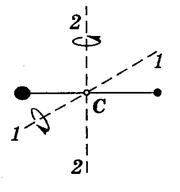Если молекула двухатомная и жёсткая («гантель»), то, кроме трёх поступательных степеней свободы, она имеет и две вращательные степени свободы, связанные с углами поворота вокруг двух взаимно перпендикулярных осей 1–1 и 2–2, проходящих через центр масс С.

Такимобразом, жёсткая двухатомная молекула имеет пять степеней свободы.

Если молекула упругая, то возможны колебания атомов и необходима ещё одна степень свободы (расстояние между атомами) – колебательная степень свободы.

Так как средняя энергия поступательного движения молекулы равна 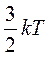, то получается, что на каждую степень свободы в среднем приходится энергия 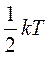. На колебательную степень свободы должны приходиться в среднем по две половинки – одна в виде кинетической и одна в виде потенциальной.

Для полной средней энергии молекулы имеем:

, где

i =z _пост + z _вр + 2 z _кол .

Число i совпадает с числом степеней свободы только для жёстких молекул.

Молекулы идеального газа не взаимодействуют между собой. Поэтому внутреннюю энергию некоторого количества идеального газа можно найти как сумму средних энергий всех молекул газа:

.

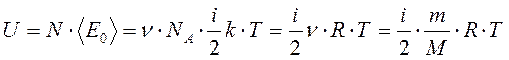Длиной свободного пробега молекулы газа λ называют среднее расстояние, которое пролетает молекула между очередными её столкновениями с другими молекулами газа.

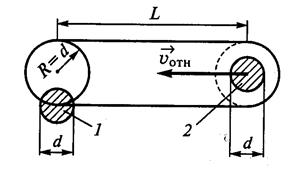Для оценки λ будем считать, что молекулы идеального газа представляют собой твёрдые шары диаметром d, которые взаимодействуют между собой только путём упругих соударений при непосредственном соприкосновении. При рассмотрении взаимодействия двух молекул систему отсчёта свяжем с центром молекулы 1. В этой системе отсчёта молекула 2 движется со скоростью и проходит расстояние L c момента предыдущего столкновения с молекулой 1. Молекула 2 не испытает ни одного столкновения с другими молекулами, если не будет ни одного их центра внутри цилиндра с площадью основания πR² = π d ² и длиной L.

Таким образом, на одну молекулу газа в среднем приходится объём

.

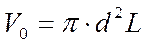Так как концентрацию п молекул газа можно представить в виде

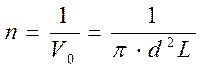, то .

Если в лабораторной системе отсчёта средняя скорость молекул равна 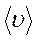, а средняя относительная скорость молекулы 2 в системе отсчёта, связанной с молекулой 1 равна , то длина свободного пробега λ и расстояние L будут связаны соотношением

.

Если υ ₁ и υ ₂ – скорости молекул 1 и 2, а φ – угол между направлениями векторов этих скоростей то

.

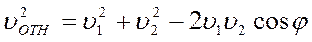Так как скорости молекул могут иметь любые произвольные направления, а их средние значения в равновесном газе одинаковые, то усреднение последнего соотношения по всем возможным углам φ даёт

.

Считая, что средние квадраты скоростей молекул пропорциональны квадратам их средних скоростей, получаем

.

Выражение для длины свободного пробега принимает вид

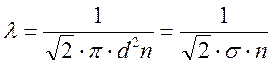, где

– эффективное сечение взаимодействия.

Средняя частота соударений молекулы газа с другими молекулами

.

Дата добавления: 2015-05-09