Машинные коды алгебраических чисел

В ЭВМ используются, в основном, следующие коды чисел: прямой, обратный и дополнительный.

Если А — число с фиксированной запятой, |A| < 1;

[A]_п — прямой код числа, который образуется по следующему правилу:

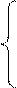А, при А ≥ 0,

[A]_п = (1.1)

1 – A, при А < 0.

В машинных кодах знаки чисел отображаются с помощью двоичных цифр. Принято обозначать

ЗН. ”+”:= 0.; ЗН. ” — ”:= 1.

Пример. А= +.101101; [A]_п = 0.101101

А= -.101101; [A]_п = _1.000000

-.101101

1.101101

Представление чисел в прямом коде используется в ЭВМ при вводе и выводе, при хранении данных в ЭВМ (не всегда). Достоинством прямого кода является простота и привычность представления чисел в виде модуля числа и знака. Однако применение прямого кода для реализации алгебраических операций не очень удобно. Рассмотрим примеры выполнения операций сложения и вычитания в прямых кодах.

S1 = A + B; S2 = A - B; A=37/64; B=19/64.

A= +.100101; B= +. 010011

111 – переносы 1 – заем

[A]_п = 0.100101 [A]_п = 0.100101

[B]_п = 0.010011 [B]_п = 0.010011

[S1]_п = 0.111000 [S2]_п = 0.010010

S1=56/64 S2=18/64

Как следует из этих примеров, сложение и вычитание различаются правилами образования переноса и заема. Это означает, что при разработке схем арифметического блока нужно будет строить не только сумматоры, но и вычитатели, т.е. специальные схемы, реализующие операцию вычитание. Такое техническое решение приведет к увеличению аппаратуры и практически не применяется.

Более широко для реализации алгебраических операций используются специальные коды, которые позволяют заменить операцию вычитание — сложением. При этом оказывается возможным при построении арифметических устройств использовать только сумматоры.

Обратный код числа образуется по следующему правилу:

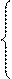[A]_о = [A]_п, при А≥0,

[A]_о = (1.2)

[A]_о = 10 + A - 10^-n, при А<0

Например, А = -.101101

[A]_о = _10.000000

.101101

_1.010011

.000001

1.010010.

Как видно из этого примера для получения обратного кода все цифры числа инвертируются. По этому же правилу осуществляется перевод обратного кода в прямой код.

Дополнительный код числа образуется по следующему правилу:

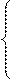[A]_п, при А ≥ 0

[A]_д = (1.3)

10 + A, при А<0

Пример образования дополнительного кода отрицательного числа

А= -7/16 = -0.0111 [A]_д = _10.0000

.0111

1.1001

Анализ правил образования обратного кода (1.2) и дополнительного кода (1.3) показывает, что для двоичной системы счисления является справедливым следующее соотношение:

[A]_д = [A]_о + 2^-n. (1.4)

На практике для нахождения дополнительного кода используют соотношение (1.4), а не (1.3).

Дата добавления: 2015-05-09