Алгоритм типа ПП

Алгоритмы алгебраического сложения и вычитания

Модифицированные коды

Одним из наиболее распространенных и достаточно простых способов обнаружения переполнения является использование модифицированных кодов. Они отличаются тем, что для представления знака используются два разряда. При этом формат числа имеет следующий вид:

№ разряда					..........	n
Значение	ЗН[0]	ЗН[1]	2^-1	2^-2	..........	2^-(n-1)

Пусть некоторое число обозначено А, тогда связь между цифрами в знаковых разрядах и величиной и знаком числа А выглядит следующим образом:

ЗН[0]	ЗН[1]
		|S|<1	S>0
		|S|<1	S<0
		|S|≥1	S>0
		|S|≥1	S<0

Как следует из этой таблицы, несовпадение цифр в знаковых разрядах означает переполнение разрядной сетки. Рассмотренные выше правила выполнения операций сложения и вычитания справедливы также и при использовании модифицированных кодов.

Рассмотрим сначала указанные операции для чисел в форме с фиксированной запятой. Конкретные алгоритмы, которые используются для выполнения этих операций в арифметическо-логических устройствах (АЛУ), зависят от многих факторов, основными из которых являются:

- в каких кодах числа хранятся в оперативном запоминающем

устройстве (ОЗУ);

- в каких кодах выполняется операция вычитание.

В зависимости от этих факторов существуют алгоритмы следующих типов:

ПП - числа в ОЗУ хранятся в прямом коде, операция вычитание выполняется также в прямом коде;

ПД(ПО) – числа в ОЗУ хранятся в прямом коде, операция вычитание выполняется в дополнительном (обратном) коде;

ДД(ОО) - числа в ОЗУ хранятся в дополнительном (обратном) коде, операция вычитание выполняется также в дополнительном (обратном) коде.

Основной особенностью этого алгоритма является то, что он аналогичен методу десятичного ручного счета. Как известно, ручное сложение-вычитание выполняется по следующим правилам:

- вычисления осуществляются над модулями чисел;

- действие над модулями определяется на основе анализа вычислительной операции (действия) и знаков чисел;

- выполняется действие над модулями;

- если действие над модулями вычитание, то из большего модуля вычитается меньший;

- знак результата определяется логическим способом в зависимости от действия над модулями, соотношения модулей и знаков исходных чисел.

Рассмотрим S=A ± B ïA ê< 1 êB ê< 1 A≠0 B≠0

Для того, чтобы формализовать постановку задачи, введем обозначения:

Действие сложение - D:=0

Действие вычитание - D:=1

Сложение модулей - DM:=0

Вычитание модулей - DM:=1

Знак числа - ¢+¢:=0

Знак числа - ¢-¢:=1

Соотношение êA ê³ êB ê соответствует W:=1

При êA ê< êB ê принято W:=0

Зададим условия этой задачи в виде таблицы истинности (табл. 1.1), в которой описаны все варианты исходных данных.

Таблица 1.1

ЗН A	ЗН B	D	DM	ЗН S
				W:=1	W:=0

В этой таблице истинности входными переменными являются ЗНА, ЗНВ, D, а выходными переменными - DM и ЗНS. После анализа данных в таблице можно сделать заключение, что действие над модулями DM является двоичной суммой трех входных переменных, а именно

DM = SM (ЗНА, ЗНВ, D) (1.7)

Таким же образом составим логическое выражение для знака суммы

ЗНS:= W & ЗНA Ú 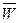& DM & 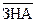Ú 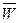& & 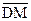ЗНA (1.8)

Сформулируем теперь в словесном виде алгоритм типа прямой-прямой (ПП), в соответствии с которым должны осуществляться преобразование и анализ кодов двоичных чисел при выполнении в АЛУ операции S = A ± B.

1) Ввод из ОЗУ в АЛУ [А]_п и [В]_п.

2) Определение DM по табл. 1.1.

3) Если DM=0, то êSê= êАê+êВê,

если перенос p =1, то имеется переполнение разрядной сетки сумматора. В противном случае перенос p =0 и переход к п. 5), иначе

4) Если DM:=1, то выполняется вычитание модулей, причем

сначала определяется êS ê= êA ê- êB ê и, если p =0, то êA ê³ êB ê и переход к п.5), иначе находится êS ê = êB ê- ï A ï и êA ê< êB ê

5) Определение ЗНS и запись результата в память.

Выполним, пользуясь этим алгоритмом,

пример:

Вычислить S = A + B A =.01011 B = -.10101

Следовательно [A]_п = 0.01011 [B]_п = 1.10101

Определим DM. Так как D:= 0 ЗНA:=0 ЗНB:=1,

то на основании (1.1)

DM = SM (0,0,1) = 1

Теперь выполним вычитание модулей

ïA ê _=.0 1 0 1 1

êB ê =.1 0 1 0 1

1.1 0 1 1 0

так как р=1, то êAê< êBê и следует выполнить вычитание

модулей в обратном порядке:

êB ê=.1 0 1 0 1

-

êA ê=. 0 1 0 1 1

êS ê=. 0 1 0 1 0

Очевидно, что знак результата ЗНS = ЗНВ.

В память должен заноситься прямой код результата, т. е.

[S]п = 1. 0 1 0 1 0

В обычной записи сумма выглядит следующим образом:

S = -. 0 1 0 1 0

Выполним некоторую качественную оценку данного алгоритма..Достоинством является то, что числа вводятся в память в прямых кодах и все вычислительные операции выполняются также в прямых кодах. Благодаря этому отсутствуют промежуточные преобразования кодов, что способствует повышению быстродействия.

Недостатком является необходимость использовать в АЛУ, кроме сумматоров, многоразрядные вычитатели, что приводит к увеличению оборудования.

Дата добавления: 2015-05-09