Проблема идентификации

Классификация переменных

В эконометрике используется множество различных видов переменных. Можно даже сказать, что для каждого типа задач применяются свои типы переменных. Итак, какие типы переменных используются в эконометрике чаще всего?
1. Экзогенные и эндогенные. Значения экзогенных задаются извне, это независимые переменные, которые "объясняют" значение результата. Эндогенной называют переменную, которая находится в результате расчета по построенной модели при заданных экзогенных переменных.
2. Лаговые переменные - это переменные, при анализе текущего периода значения которых должны быть взяты не за текущий, а за отстоящий от него на определенное расстояние (количество периодов, лаг) предыдущий период. Хорошим примером может стать выработка работника и его заработная плата: сначала работник производит продукцию, и лишь спустя определенное время ему выплачивают заработную плату.
3. Предопределенные переменные. Это экзогенные переменные вместе с их лаговыми значениями и лаговые значения эндогенных переменных в предыдущие моменты времени, которые служат для нахождения значений эндогенных переменных в данный момент времени.
4. По принимаемым значениям (в зависимости от применяемой шкалы измерения) переменные делят на наименования (продаваемые квартиры расположены в районах, имеющих наименования), порядковые (оценки в школе: можно сказать, что 4 больше, чем 3, но нельзя сказать, что разница между 4 и 3 такая же, как и между 5 и 4), измеренные по шкале интервалов (когда можно сказать, на сколько А больше чем Б, но невозможно сказать, во сколько раз А больше, чем Б) и измеренные по шкале отношений (возможно не только установление отношений между свойствами или качествами, но и определение интервала и даже отношений между свойствами объектов).

При переходе от приведенной формы модели к структурной исследователь сталкивается с проблемой идентификации. Идентификация – единственность соответствия между структурной и приведенной формами модели.

Параметры структурной формы модели по оценкам приведенных коэффициентов можно определить не всегда. Для этого необходимо, чтобы модель была идентифицируемой.

С позиции идентифицируемости структурные модели можно подразделить на три вида:

Выделяют:

1) Точно идентифицируемая модель – все ее уравнения точно идентифицированы. То есть все структурные коэффициенты определяются однозначно (единственным способом) по коэффициентам приведенной формы модели. И число параметров структурной модели равно числу параметров приведенной формы.

2) Неидентифицируемая модель – число приведенных коэффициентов меньше числа структурных коэффициентов. Оценки всех структурных параметров невозможно найти по коэффициентам приведенной модели.

3) Сверхидентифицируемая модель – число приведенных коэффициентов больше числа структурных коэффициентов (на основе приведенной формы можно получить 2 и более значений одного структурного коэффициента). Практически решаема, но требует применения специальных методов.

На идентификацию проверяются все уравнения модели. Модель считается идентифицируемой, если все уравнения идентифицируемы; сверх – если хоть одно сверхидентифицируемо, а остальные точно идентифицируемы. Если среди всех уравнений модели есть хотя бы одно неидентифицированное, то вся модель считается неиденти­фицированной.

Правила идентификации

Введем следующие обозначения:

М- число экзогенных (предопределенных) переменных в модели;

т- число экзогенных (предопределенных) переменных в данном уравнении;

К - число эндогенных переменных в модели;

k - число эндогенных переменных в данном уравнении.

А) Необходимое (но недостаточное) условие идентификации.

Для того чтобы уравнение модели было идентифици­руемо, необходимо, чтобы число предопределенных пере­менных, отсутствующих в данном уравнении, было не меньше «числа эндогенных переменных, входящих в уравнение минус 1», т.е.: ;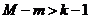

Если 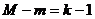, уравнение точно идентифицировано.

Если 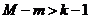, уравнение сверхидентифицировано.

Либо D+1=H (H – число эндогенных переменных в уравнении; D – число отсутствующих экзогенных переменных).

Эти правила следует применять к структурной форме модели.

Достаточное условие идентификации. Введем обозначения: А - матрица коэффициентов при переменных не входящих в данное уравнение.

Достаточное условие идентификации заключается в том, что

- определитель матрицы А должен быть не равен нулю,

- ранг матрицы А должен быть не меньше, чем число эндогенных переменных в системе без одного .

Ранг матрицы - размер наибольшей ее квадратной подматрицы, определитель которой не равен нулю.Пример:

a b

c d 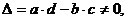тогда ранг R=2.

Сформулируем необходимое и достаточное условия идентификации:

1) Если 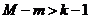и ранг матрицы А 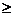равен , то уравнение сверхидентифицировано.

2) Если 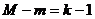и ранг матрицы А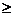 , то уравнение точно идентифицировано.

3) Если 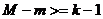и ранг матрицы А < то уравнение неидентифицированно.

4) Если 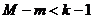, то уравнение неидентифицированно. В этом случае ранг матрицы А будет меньше .

Дата добавления: 2015-05-09