Интерпретация уравнения регрессии

Графический способ. Численный способ

Парная регрессия и корреляция

Парная регрессия представляет собой регрессию между двумя переменными – и, т. е. модель вида:,

где – зависимая переменная (результативный признак);

– независимая, или объясняющая, переменная (признак-фактор).

Между переменными и нет строгой функциональной зависимости, поэтому практически в каждом отдельном случае величина складывается из двух слагаемых:

,

где – фактическое значение результативного признака;

– теоретическое значение результативного признака, найденное исходя из уравнения регрессии;

– случайная величина, характеризующая отклонения реального значения результативного признака от теоретического, найденного по уравнению регрессии.

Случайная величина называется также возмущением. Она включает влияние не учтенных в модели факторов, случайных ошибок и особенностей измерения. Ее присутствие в модели порождено тремя источниками: спецификацией модели, выборочным характером исходных данных, особенностями измерения переменных.

От правильно выбранной спецификации модели зависит величина случайных ошибок: они тем меньше, чем в большей мере теоретические значения результативного признака, подходят к фактическим данным.

К ошибкам спецификации относятся неправильный выбор той или иной математической функции для и недоучет в уравнении регрессии какого-либо существенного фактора, т. е. использование парной регрессии вместо множественной.

В парной регрессии выбор вида математической функции может быть осуществлен тремя методами:

графическим;

аналитическим, т.е. исходя из теории изучаемой взаимосвязи;

Этот метод применяют для наглядного изображения формы связи между изучаемыми экономическими показателями. Для этого в прямоугольной системе координат строят график, по оси ординат откладывают индивидуальные значения результативного признака Y, а по оси абсцисс - индивидуальные значения факторного признака X.

Совокупность точек результативного и факторного признаков называется полем корреляции.

Интерпретация моделей регрессии осуществляется методами той отрасли знаний, к которой относится исследуемое явление. Но всякая интерпретация начинается со статистической оценки уравнения регрессии в целом и оценки значимости входящих в модель факторных признаков.

Прежде всего необходимо рассмотреть коэффициенты регрессии. Чем больше величина коэффициента регрессии, тем значительнее влияние данного признака на моделируемый.

Знаки коэффициентов регрессии говорят о характере влияния на результативный признак. Если факторный признак имеет знак плюс, то с увеличением данного фактора результативный признак возрастает; если факторный признак имеет знак минус, то с его увеличением результативный признак уменьшается.

Если экономическая теория подсказывает, что факторный признак должен иметь положительное значение, а он имеет знак минус, то необходимо проверить расчеты параметров уравнения регрессии. Такое явление чаще всего бывает в силу допущенных ошибок при решении. Однако следует иметь ввиду, что когда рассматривается совокупное влияние факторов, то в силу наличия взаимосвязей между ними характер их влияния может меняться.

23 Оценка существенности параметров регрессии: F -критерий, t -критерий.

С помощью критерия Фишера оценивают качество регрессионной модели в целом и по параметрам.

Для этого выполняется сравнение полученного значения F и табличного F значения. F-критерия Фишера. F фактический определяется из отношения значений факторной и остат очной дисперсий, рассчитанных на одну степень свободы:

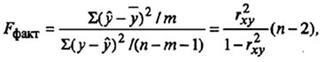
где n - число наблюдений;

m - число параметров при факторе х.

Если Fтабл > Fфакт то признается статистическая незначимость модели, ненадежность уравнения регрессии.

Критерии Стьюдента

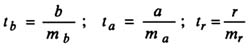
Случайные ошибки коэффициентов линейной регрессии и коэффициента корреляции определяются по формулам:

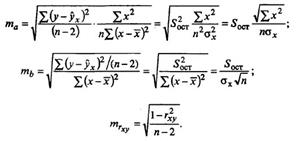
Дата добавления: 2015-05-09