Спектрального анализа

Основные понятия, задачи и проблемы цифрового

Обращение к читателю

Благодарности

Считаем своим долгом выразить признательность

Мазалецкой А.Л., любезно предоставившей в наше распоряжение материалы своих исследований по методам ЦСА, основанным на линейном моделировании исследуемого сигнала;

Банько В.В., согласившемуся помочь нам в апробировании и детализации методов корелограмного анализа;

Анджану С.Э., работавшему непосредственно со студентами и давшему немало ценных замечаний и советов, улучшивших восприятие материала;

студентам Горохову М. и Масленниковой Н., изучавшим в 1994-1995 гг. рукописи отдельных разделов, чьи замечания и предложения способствовали улучшению материала;

всем сотрудникам лаборатории радиоэлектроники, научно-исследовательская работа которых позволила наконец-то в конце 1995 г. приступить к распечатке первых экземпляров настоящего пособия;

нашим редакторам и рецензентам.

Уважаемый читатель! Настоящее учебное пособие, как и остальные, уже известные тебе, создано долгим и кропотливым трудом многих людей. И, конечно, оно не лишено недостатков. Работая с книгой, ты, возможно, обнаружишь ошибки и места, сложные для понимания. Неоценимой услугой для авторов будут твои замечания и предложения, которые будут учтены в следующей редакции пособия, запланированной на второе полугодие 1996 г.

С благодарностью, авторы.

При обработке сигналов во многих случаях приходится измерять спектры. Понятие "спектральный анализ" включает в себя большое число различных измерений. В широком смысле его можно определить как "измерение, которое дает точные или приближенные значения z -преобразования дискретного сигнала для заданных значений z". Создание адекватной теории спектрального анализа затруднено тем обстоятельством, что на практике все спектральные измерения проводятся на конечных временных интервалах, длина которых часто выбирается интуитивно на основе накопленного опыта. В этом случае часто используется термин "оценка", а не "измерение".

1.1. Что такое цифровой спектральный анализ

Термин "цифровой спектральный анализ" отражает тип исследуемого колебания и используемый математический аппарат. Так, исследуемое колебание может быть дискретным или цифровым, а используемый математический аппарат должен обеспечивать разложение исследуемого колебания по дискретной или цифровой системе базисных функций. Математический аппарат, в зависимости от метода анализа, базируется, в основном, на дискретном преобразовании Фурье, z-преобразовании, дискретной свертке, разностных уравнениях, линейном моделировании.

В литературе термин "цифровой спектральный анализ" относят как к обработке дискретных сигналов, так и цифровых. Строго говоря, обработке дискретных сигналов должен соответствовать термин "дискретный спектральный анализ", где представление значений как исследуемого сигнала, так и различных констант и переменных является точным. Мы, как и принято в литературе, будем пользоваться одним термином "цифровой спектральный анализ". Какой тип сигнала анализируется - будет ясно из дальнейших рассуждений.

Спектральный анализ, и цифровой в частности, не ограничивается задачей определения спектра исследуемого сигнала - совокупности коэффициентов разложения по выбранной системе базисных функций. Так, при ЦСА решаются задачи оценки частоты спектральных линий, совместной оценки спектральной плотности случайного процесса и амплитуд спектральных линий детерминированного сигнала и ряд других. Мы говорим об оценке, т. к. в случае цифровой обработки возникают специфические искажения как исследуемого сигнала, так и результатов анализа, что не позволяет произвести точные измерения. В ряде случаев искажения (например, эффект наложения) возникают и при дискретном анализе. Данное обстоятельство заставляет особое внимание уделять интерпретации результатов анализа, а в некоторых случаях и их адекватности результатам соответствующего континуального анализа. Последняя проблема возникает, когда цифровой сигнал получен из континуального прототипа.

Поскольку ЦСА является численным методом анализа, то его конкретная реализация зависит от способа получения и представления исследуемого сигнала и аппаратной реализации вычислительных средств. Основными областями применения ЦСА являются математическое моделирование, обработка полученных ранее экспериментальных данных и обработка данных, получаемых непосредственно в процессе анализа. Последняя область применения - аппаратурный ЦСА, функционирующий, как правило, в условиях ограничения времени анализа. В качестве цифровых вычислительных устройств, реализующих алгоритмы анализа, могут быть использованы универсальные ЭВМ, специализированные сигнальные процессоры с плавающей и фиксированной запятой. В задачах аппаратурного ЦСА используются высокопроизводительные сигнальные процессоры с плавающей запятой или целочисленной арифметикой.

Классификация алгоритмов анализа, используемых в задачах ЦСА, приведена на рис. 1.1.

Алгоритмы, основанные на цифровой фильтрации, реализуются с помощью различных схем цифровых фильтров.

Алгоритмы, основанные на быстром преобразовании Фурье (БПФ), являются высокоэффективными методами.

Часть методов, объединенных под общим названием классических, использовалась уже на первых порах создания цифрового спектрального анализа. Они хорошо разработаны, относительно просты и удобны, легко реализуются программно. Дают статистически устойчивые (состоятельные) оценки. Недостатки этих методов заключаются в довольно широком круге ограничений и искажениях спектра, связанных с обработкой конечных последовательностей.

Перечисленные недостатки устраняются в методах спектрального анализа в заданном секторе z -плоскости. Они позволяют получать оценки z -преобразования в точках произвольного контура или, что то же, оценки спектральных составляющих в точках, произвольным образом расположенных на частотной оси.

Методы, основанные на моделировании исследуемого сигнала выходным сигналом линейного фильтра (авторегрессионные, АР-методы) или рядом комплексных экспонент (метод Прони) являются относительно новыми в практике ЦСА и получили признание благодаря высокой точности и, что особенно важно, высокому разрешению спектральных оценок.

Математические основы всех этих алгоритмов различны.

Перечисленные алгоритмы и их особенности, возникающие при квантовании сигнала и использовании при обработке чисел с конечной разрядностью, рассматриваются в разделах 3 - 7 настоящего пособия.

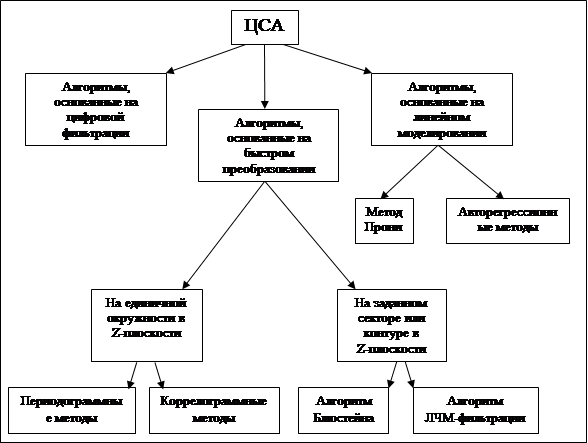Рис. 1.1

1.2. Проблемы в области спектрального оценивания

Интерес к цифровым методам спектрального анализа поддержива­ется тем улучшением характеристик, которое они обещают, а именно: высоким частотным разрешением, повышенной способностью к об­наружению слабых сигналов или же сохранением "досто­вер­нос­ти" формы спектра при меньшем числе используемых па­раметров. Аналитически описать характеристики большинства методов в случае ограниченного временного анализа (т. е. в случае корот­кой реа­ли­зации данных) весьма затруднительно, именно поэтому в ли­те­ратуре можно найти лишь очень малое количество эмпирических ре­зультатов. Это обусловило появление ряда проблем в области со­временного спектрального оценивания, некоторые из них кратко ос­вещены ниже.

1.2.1. Разрешение

Спектральное разрешение относится к числу главных проблем современного спектрального оценивания, в особенности примени­тельно к анализу коротких последовательностей данных. При этом то, что понимается под термином "разрешение", носит весьма субъек­тивный характер. Одно из ранних определений принадлежит Релею, которое исходит из следующего рабочего определения для разрешения оптических телескопов с ограниченной пространственной апертурой: "Подобно тому, как оптическая сила телескопа измеряется близостью двойных звезд, которые он может разрешить, так и оптическую силу спектроскопа следует измерять близостью самых близких двойных ли­ний в спектре, которые он может разрешить".

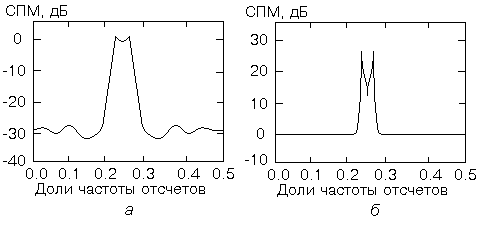Рис. 1.2

В литературе принято характеризовать относительные величины разрешающей способности двух спектральных оценок на основе визу­альных наблюдений. Рассмотрим две спектральные оценки, показанные на рис. 1.2. Спектральная оценка на рис. 1.2, а имеет единичный нормиро­ванный максимум с двумя слабо различимыми пиками, что должно ука­зывать на присутствие двух спектральных составляющих. Если теперь нелинейным масштабированием сформировать новую спектральную функцию, которая показана на рис. 1.2, б, то она будет выглядеть, как спектр с "более высоким" раз­решением. На самом же деле оба приведенных спектра несут в себе одну и ту же информацию, а это означает, что одного лишь визуаль­ного сравнения спектральных оценок, конечно же, недостаточно для суждения о характеристиках разрешения.

1.2.2. Обнаружимость сигналов

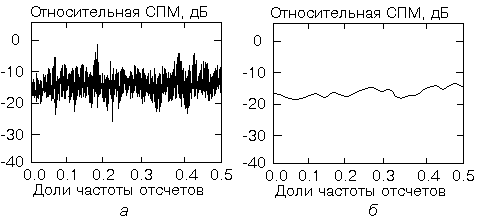Использование спектрального оценивания для обнаружения при­сутствия сигналов приводит к возникновению другой проблемы. Рас­смотрим периодограммы, показанные на рис. 1.3. Обе они соответствуют одной и той же 1024-точечной реализации некоторого процесса, со­стоящего из аддитивной смеси одной синусоиды и белого шума при отношении сигнал/шум равном -17 дБ. Периодограмма на рис. 1.3, а по­лу­чена непосредственно по всем 1024 отсчетам, и в ней над СПМ шума отчетливо видна спектральная линия синусоиды с относительной частотой 0.18. На рис. 1.3, б представлена сглаженная периодограмма, полученная в результате разбиения исходной последовательности на 32 сегмента по 32 отсчета в каждом и последующего усреднения пе­риодограмм этих сегментов. На этой оценке более очевидна равномер­ная спектральная характеристика белого шума, но отклик, обуслов­ленный присутствием синусоиды, здесь не обнаружим. Можно пока­зать, что обнаружимость сигнала по несглаженной периодограмме превышает обнаружимость этого сигнала по сглаженной периодограмме в число раз, равное примерно корню квадратному из числа сегмен­тов, или на 10lg(321/2)=7.5 дБ в рассматриваемом случае. С точки зре­ния отображения полного спектра процесса (и оценки его СПМ) лучше сглаженная спектральная оценка, показанная на рис. 1.3, б, но с точки зрения обнаружимости сигнала - лучше

Рис. 1.3

несглаженная оценка.

Таким образом, аргументы в пользу выбора той или иной спек­тральной оценки будут зависеть от того, интересует ли нас сгла­женная оценка в пределах всего диапазона анализируемых частот или же нам важна более высокая степень обнаружимости сигнала на неко­торых конкретных его участках. Поэтому алгоритмы спектрального оценивания вовсе не обязательно являются также и хорошими алго­ритмами обнаружения.

1.2.3. О разграничении понятий оценивания параметров сигнала со

спектральным оцениванием

Задача спектрального оценивания подразумевает оценивание не­которой функции частоты. О характеристиках спектральной оценки судят по тому, насколько хорошо она согласуется с известным спек­тром тест-сигнала в некоторой непрерывной области частот. Имеются приложения, где основной интерес представляет лишь локальное по­ведение спектральной оценки в некоторых заданных диапазонах ча­стот. Примером может служить оценивание частоты синусоиды в белом шуме, результаты которого представлены на рис. 1.3. Нетрудно видеть, что в качестве спектральной оценки лучше использовать оценку на рис. 1.3, б, так как она ближе к равномерному спектру белого шума. В качестве же оценки частоты синусоиды лучше использовать оценку на рис. 1.3, а, так как она позволяет более точно определить частоту этой синусоиды. К сожалению, эти оценки нередко путают в литера­туре, поскольку многие задачи оценивания параметров излагаются в контексте спектрального оценивания, даже если функция спектраль­ной оценки не является искомой количественной величиной.

Задача оценивания параметров и задача спектрального оценива­ния требуют различного статистического подхода, хотя обе они могут перекрываться в некоторых частных случаях. Поэтому о характе­ристиках спектральной оценки нельзя полностью судить по ее харак­теристикам как оценки параметров. Так, например, сравнение оце­нок, представленных на рис. 1.3, показывает, что сглаженная перио­дограмма является хорошей спектральной оценкой, но плохой оценкой параметра, которым в данном случае является частота синусоиды.

1.2.4. Состоятельность оценки

Спектральная оценка, получаемая по конечной реализации дан­ных, характеризует некоторое предположение относительно той ис­тинной спектральной функции, которая была бы получена, если бы в нашем распоряжении имелась запись данных бесконечной длины. Именно поэтому поведение и характеристики спектральных оценок должны описываться с помощью статистических терминов. Общеприня­тыми статистическими критериями качества оценки являются ее сме­щение и дисперсия, для получения которых нужна серия спектральных оценок. Если в некоторой области частот значение дисперсии ве­лико, то это свидетельствует о том, что особенности, наблюдаемые в спектре отдельной реализации, не могут считаться статистически значимыми. С другой стороны, особенности совмещен­ных спектров в тех областях, где эта дисперсия мала, с большей достоверностью могут быть соотнесены с действительными частотными составляющими анализируемого сигнала. Однако, в случае коротких записей данных часто не удается получить несколько спектральных оценок, да и сам статистический анализ отдельных спектральных оценок, полученный по коротким записям данных, в общем случае представляет собой весьма трудную проблему.

В предыдущих рассуждениях мы делали предположение о стацио­нарности анализируемого процесса. В противном случае задача спек­тральной оценки значительно усложняется.

1.3. Спектральный анализ и z -преобразование, использование ДПФ в

спектральном анализе

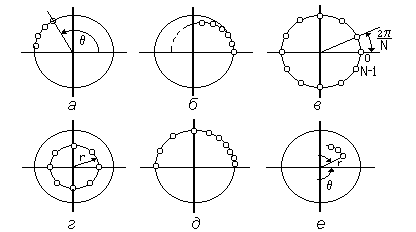Рис. 1.4

Прежде, чем приступить к измерению спектра сигнала, необходимо выяснить, что представляет собой анализируемый сигнал и что именно нужно узнать о сигнале. В общем случае задачу спектрального анализа можно рассматривать как задачу вычисления z -преобразования модифицированного сигнала в некоторой области на z -плоскости. На рис. 1.4 показаны шесть возможных областей на z -плоскости, которые с точки зрения спектрального анализа сигнала могут представлять интерес. На рис. 1.4, а, в и д эти области представляют собой совокупности точек на единичной окружности в z -плоскости. В трех остальных случаях измерения также проводятся в отдельных точках, которые, однако, не лежат на единичной окружности.

Теоретически спектр можно измерять в любой точке z1на z -плоскости. Однако, практически при таких измерениях нужно учитывать время вычисления и эффекты, обусловленные квантованием. С учетом сказанного обобщенный спектр сигнала x(n) можно определить как

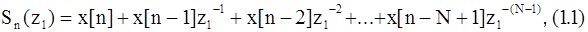
или

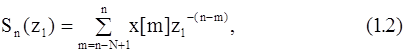
где N - число отсчетов, по которым находится оценка спектра.

Когда спектр сигнала меняется во времени, возникает необходимость измерять Sn(z1) для последовательных значений n, т. е. значения S0(z1), S1(z1), S2(z1) и т. д. Такой способ измерений называют скользящим. Он обеспечивается за счет смещения на один отсчет вперед временного окна, содержащего N отсчетов, и повторения измерения.

Анализ формул (1.1) и (1.2) показывает, что скользящее спектральное измерение в одной точке z=z1эквивалентно обработке сигнала x(n) КИХ-фильтром с импульсной характеристикой вида

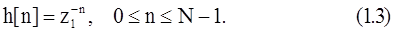
На рис. 1.5 приведена схема КИХ-фильтра для вычисления прямой свертки, обеспечивающая спектральные измерения в соответствии с формулой (1.2).

Проанализировав выражения для двух последовательных спектральных измерений Sn-1(z1) и Sn(z1), можно получить следующую рекуррентную формулу

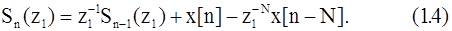
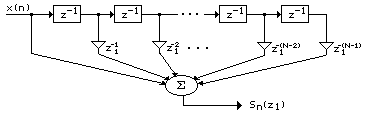Рис. 1.5

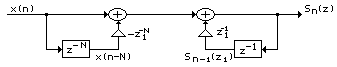Схема фильтра, реализующего алгоритм (1.4), приведена на рис. 1.6.

Рис. 1.6

Блоки, обозначенные на рис. 1.5 и рис. 1.6 как z-N и z-1представляют собой элементы задержки, тогда как величины, равные степеням z1, представляют коэффициенты умножителей (в общем случае они являются комплексными). Входные сигналы и промежуточные результаты фильтра тоже могут быть комплексными.

Из (1.4) и рис. 1.6 следует, что для обеспечения скользящих спектральных измерений сигнала в одной точке z=z1достаточно выполнить всего два комплексных умножения на входной отсчет.

Чтобы найти спектр сразу во многих точках, например z1, z2, z3 и т.д., необходимо повторять описанные выше вычисления для каждого нового значения z. На практике чаще всего представляет интерес поведение спектра на некоторой заданной довольно большой совокупности точек в z -плоскости. В этом случае главная задача состоит в том, чтобы выполнить измерение спектра, используя минимальное количество операций.

В подавляющем большинстве приложений задача измерения спектра сводится к нахождению значений z -преобразования конечной реализации сигнала для большого числа точек, равномерно распределенных по окружности единичного радиуса (рис. 1.4, в). Измерения такого типа соответствуют вычислению ДПФ S(k) конечной последовательности x(n) и обычно наиболее эффективно выполняются с применением алгоритмов быстрого преобразования Фурье (БПФ)

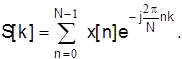
Точки zkна единичной окружности расположены с интервалом 2p/N.

Иногда желательно проводить измерения спектра, вычисляя значения z-преобразования последовательности x(n) в равноотстоящих точках, расположенных внутри единичной окружности. Так, на рис. 1.4, г представлен случай, когда все точки равномерно распределены на окружности радиуса r<1. Такое преобразование также можно получить с помощью ДПФ

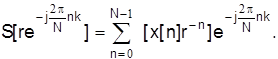
Это преобразование соответствует ДПФ последовательности x(n)r-n, поэтому в данном случае спектральный анализ сводится к предварительному умножению массива сигнала x(n) на r-n и последующему выполнению ДПФ.

1.4. Взаимная связь спектров континуальных и дискретных сигналов

Допустим, что имеется непрерывный сигнал S(t) (рис. 1.7) в виде последовательности равноотстоящих импульсов, и этот сигнал задан на интервале [0,T), на котором умещается ровно N импульсов, например, N=4. Эти импульсы можно пронумеровать. Приняв номер импульса за новую дискретную переменную n, мы можем утверждать, что тот же рис. 1.7 изображает дискретный сигнал S(n), определенный на интервале [0,N). Оба эти сигнала, непрерывный S(t) и дискретный S(n), будут иметь дискретные спектры Cн(k) и Cд(k) (рис. 1.8). Эти спектры будут отличаться друг от друга.

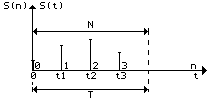Установим разницу между ними. Дискретная переменная на интервале [0,N) принимает только фиксированные значения n=0, 1, 2,..., а непрерывная переменная t на интервале [0,T) принимает всевозможные значения. Таким образом, функция S(n) задает сигнал только в четырех точках, а функция S(t) - на бесконечном множестве точек, как совпадающих с точками отсчетов, так и в паузах между ними.

Рис. 1.7

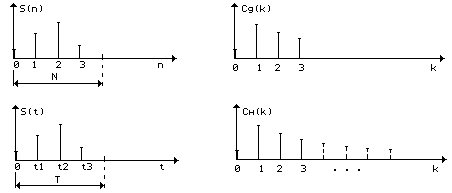Рис. 1.8

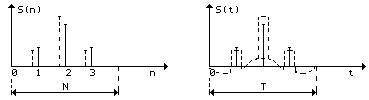Рис. 1.9

Из этого различия вытекает важная особенность: разложение сигнала S(n) можно проводить только по системе дискретных решетчатых функций {h(k,n)}, а разложение сигнала S(t) - только по системе непрерывных функций {h(k,t)}. Спектры Cд(k) и Сн(k), полученные при таких разложениях (рис. 1.8), будут отличаться друг от друга тем, что спектр Cд(k) будет содержать только 4 (по числу степеней свободы дискретного сигнала), а спектр Сн(k) - бесконечное множество компонент, т. к. непрерывный сигнал S(t) имеет бесконечную размерность. Однако, поскольку сигнал S(t) задан на конечном интервале [0,T), его спектр будет дискретным. В отличие от спектра Cд(k), коэффициенты разложения Сн(k) будут бесконечно малыми, так как сигнал S(t) имеет бесконечно малую среднюю мощность (вследствие этого изображение спектра Сн(k) на рис. 1.8 является условным).

Чтобы продемонстрировать различие спектров Cд(k) и Сн(k), проведем следующий мысленный эксперимент. Опустим из этих спектров составляющую с одним и тем же номером. Это вызовет искажения сигнала (рис. 1.9), но в случае дискретного сигнала эти искажения будут выражаться только в изменении величин отсчетов (пунктирные линии), а в случае непрерывного сигнала помимо таких изменений в паузах между отсчетами еще появляются колебания.

Несмотря на указанное различие, спектры Cд(k) и Сн(k) принадлежат родственным сигналам и имеют некоторую общность, а именно: первые N коэффициентов разложения в этих спектрах совпадают с точностью до постоянного множителя.

Покажем, что это действительно так. Непрерывный сигнал S(t) может быть записан в виде

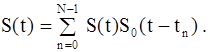
Перейдем к нормированному непрерывному времени t=t/Dt и нормированному дискретному времен и n=[t/Dt], где Dt - интервал дискретизации, а [b] обозначает целую часть числа b, и введем дельта-функцию:

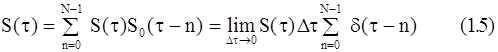
Спектр непрерывного сигнала S(t) будет определяться выражением

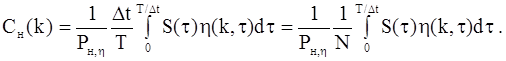
Подставим сюда выражение (1.5) для сигнала S(t) в виде ряда Фурье:

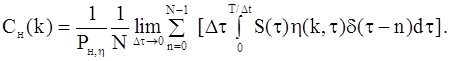
Учитывая фильтрующее свойство дельта-функции, получим

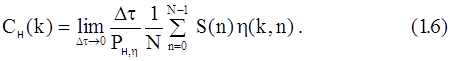
Ранее было показано, что разложение дискретного сигнала имеет вид:

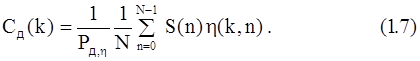
Сравнив (1.6) и (1.7), замечаем, что при kÎ[0,N-1] спектры Сн(k) и Cд(k) совпадают с точностью до масштабного коэффициента. Из этого результата следует также, что у всех непрерывных огибающих данного дискретного сигнала с N отсчетами первые N/2 составляющих спектра совпадают с точностью до постоянного множителя. Таким образом, спектр дискретного сигнала одновременно определяет ансамбль непрерывных сигналов, порождающих данный дискретный сигнал. Чтобы выбрать из этого ансамбля конкретный непрерывный сигнал, необходимо знать дополнительно составляющие спектра при k³N, которые отличают спектр непрерывной огибающей от спектра самого дискретного сигнала.

При разложении дискретного сигнала в ряд Фурье по системе комплексных экспоненциальных функций {ejkn2p/N} спектр является периодическим с периодом N. Другими словами, периодический дискретный сигнал S(n) и его спектр C(k) обладают свойством

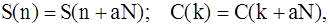
где N - период, а b - произвольное целое число.

Действительно, спектр периодического дискретного сигнала при разложении по системе функций {ejkn2p/N} может быть записан в виде

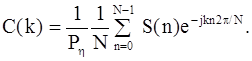Отсюда имеем

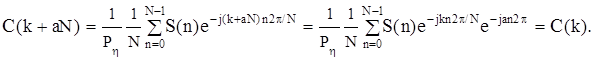
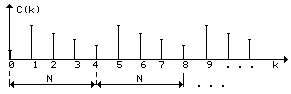Рис. 1.10

При переходе от дискретного сигнала к непрерывному число отсчетов в одном периоде N®¥, поэтому по мере приближения дискретного сигнала к непрерывному период его спектра будет неограниченно возрастать. В пределе, при N®¥ получим известную картину: периодический непрерывный сигнал имеет линейчатый, но непериодический спектр.

Дата добавления: 2015-05-09