Моделировании исследуемого сигнала 1 страница

Спектральный анализ, основанный на линейном

В разделах 3 - 5 СПМ была определена как дискретно-временное преобразование Фурье (ДВПФ) бесконечной автокорреляционной последовательности (АКП). Это соотношение между СПМ и АКП можно рассматривать как непараметрическое описание статистик второго порядка случайного процесса. Частным случаем такого описания можно считать оценку СПМ в одной точке z-плоскости (раздел 6).

К параметрическому описанию статистик второго порядка можно прийти, рассматривая модель временного ряда, соответствующего анализируемому случайному процессу. В этом случае СПМ модели временного ряда будет прежде всего некоторой функцией параметров этой модели, а не АКП. Методы, рассматриваемые в данном разделе, применимы только к частному классу моделей, возбуждаемых белым шумовым процессом и обладающих рациональной системной функцией. Этот класс включает модель авторегрессионного процесса (АР), модель процесса скользящего среднего (СС) и модель процесса авторегрессии-скользящего среднего (АРСС). Выходные процессы моделей этого класса имеют спектральные плотности мощности, которые полностью описываются с помощью парамет- ров модели и дисперсии белого шумового процесса. Значения этих парамет- ров и дисперсии белого шума определяются из выборки исследуемого процесса при помощи методов, основанных на линейном моделировании.

Причины применения параметрических моделей: возможность получения на их основе более точных оценок СПМ и более высокого спектрального разрешения, чем это возможно с помощью классических методов спектрального оценивания. Степень улучшения разрешения и повышения достоверности спектральных оценок определяется соответствием выбранной модели анализируемому процессу и возможностью аппроксимации исходных данных или АКП (известной или оцененной по этим данным) с помощью нескольких параметров модели.

Методика спектрального оценивания, основанная на моделировании исследуемого процесса, состоит из трех этапов: выбора параметрической модели фильтра; определения параметров модели; оценки СПМ модели процесса.

7.1. Модели случайных процессов

Многие последовательности, представляющие собой сумму детерминированных и случайных последовательностей, могут быть достаточно хорошо аппроксимированы выходным сигналом линейного дискретного фильтра с рациональной системной функцией, возбуждаемого белым шумом с нулевым средним и дисперсией s2.

При решении задачи моделирования требуется обеспечить устойчивость и (или) каузальность применяемого фильтра с тем, чтобы получить однозначно определенную модель.

Существует три типа моделей, описывающих такой фильтр.

1) Самая общая модель - модель авторегрессии-скользящего среднего(АРСС) описывается линейным разностным уравнением с комплексными коэффициентами

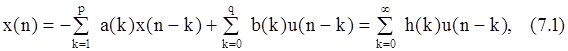
где x(n) - выходная последовательность моделирующего фильтра, u(n) - возбуждающая шумовая последовательность. Без потери общности можно положить b(0)=1 и суммировать с k=1, так как u(n) всегда можно соответствующим образом промасштабировать, чтобы учесть любой коэффициент усиления фильтра.

Функциональная схема АРСС-модели приведена на рис. 7.1, а. Здесь параметры a(k) характеризуют авторегрессионную часть модели, а b(k) - часть, соответствующую скользящему среднему.

Системная функция фильтра определяется выражением

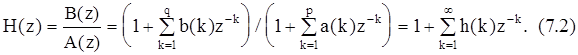
Предполагается, что нули полиномов A(z) и B(z) расположены внутри единичной окружности в z-плоскости, что гарантирует принадлежность функции H(z) устойчивому фильтру. Подставив сюда z=exp(j2pfT), после масштабирования интервалом отсчетов T получим СПМ для АРСС-модели:

где полиномы A(f) и B(f) определяются выражениями

а векторы параметров a и b имеют вид

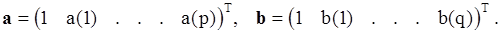
СПМ АРСС-процесса вычисляется в диапазоне частот -1/2£Tf£1/2T.

В литературе часто используется обозначение АРСС(p,q) - АРСС-модель с АР-параметрами порядка p и СС-параметрами порядка q. Задание АР-, СС-параметров и дисперсии белого шума s2полностью характеризует СПМ АРСС-процесса x(n).

а)

б)

в)

Рис. 7.1

2) Модель процесса скользящего среднего порядка q, или СС(q)- модель получается из АРСС-модели при нулевых (за исключением a(0)=1) АР-параметрах

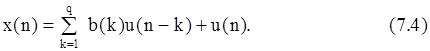СПМ СС-процесса

Функциональная схема СС-процесса показана на рис. 7.1, б.

3) Модель авторегрессионного процесса порядка p, или АР(p)-модель получается из АРСС-модели при нулевых (за исключением b(0)=1) СС- параметрах:

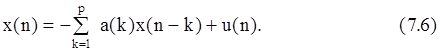СПМ АР-процесса

Функциональная схема АР-модели приведена на рис. 7.1, в.

На рис. 7.2 показаны спектры типичных АРСС-, СС- и АР-процессов. Выбор одной из трех моделей требует некоторых предварительных сведений о возможной форме спектральной оценки. Если необходимы спектры с острыми пиками, но без глубоких нулей, то подходит АР-модель. Если, наоборот, необходимы спектры с глубокими нулями, но без острых пиков, лучше взять СС-модель. АРСС-модель пригодна в обоих случаях. В спорных ситуациях следует использовать ту модель, которая имеет наименьшее число параметров. Этот принцип экономии был предложен Боксом и Дженкинсом и основан на том факте, что получить оценки с хорошими статистическими свойствами можно, как правило, тогда, когда число оцениваемых параметров минимально. В дальнейшем речь пойдет об АР-моделях, что обусловлено двумя причинами:

1) АР-спектры имеют острые пики, а это связано со спектральным разрешением;

2) оценки АР-параметров можно получить как решения линейных уравнений (в отличие от СС-параметров), следствием чего явилось множество хорошо разработанных алгоритмов их нахождения.

Рис. 7.2, а - АР-спектр, б - СС-спектр, в - АРСС-спектр.

Существует теорема декомпозиции:

Если задана АР-, СС- или АРСС-модель с конечным числом параметров, то ее можно выразить через две другие модели.

АРСС-и СС-процессы можно записать с помощью одной АР-модели в общем случае бесконечного порядка.

Так, пусть

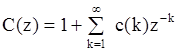
- полином знаменателя АР(¥)-модели, эквивалентной заданной АРСС(p,q)-модели. Параметры АР-модели находятся с помощью равенства системных функций АРСС(p,q)- и АР(¥)-моделей

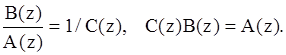
Отсюда параметры АР(¥)-модели с начальными условиями c(-1)=...=c(-q)=0:

Замечание.

Рассмотрим z-преобразование АР-процесса

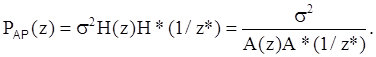
Полюсы PАР(z) будут комплексно-сопряженными взаимнообратными парами. С точки зрения оценки СПМ можно не требовать, чтобы полином A(z) являлся минимально-фазовым полиномом (все нули и полюсы которого лежат в единичной окружности в z-плоскости). Но так как для реализации фильтра нам приходится использовать оценки его коэффициентов, то встает вопрос об устойчивости и полином A(z) должен являться минимально-фазовым, что может быть сделано посредством инверсного переноса всех его полюсов, расположенных вне единичной окружности, внутрь ее.

7.2. Методы оценки параметров АР-моделей. Блочные алгоритмы

Методы оценки АР-параметров можно разбить на две категории: алгоритмы для обработки блоков данных и алгоритмы для обработки последовательных данных.

Алгоритмы блочной обработки предназначены для обработки целых блоков накопленных отсчетов данных некоторого фиксированного объема. Блочные методы можно кратко описать как алгортмы с фиксированным временем, рекурсивные относительно порядка в том смысле, что позволяют рекурсивным образом получать оценки параметров АР-модели более высокого порядка по оценкам параметров модели более низкого порядка. Такие алгоритмы целесообразно применять в тех случаях, когда порядок требуемой модели неизвестен и необходимо испытывать модели различных порядков и сравнивать результаты.

АР(p)-процесс имеет три экивалентных представления:

1) в виде бесконечно протяженной АКП;

2) в виде конечной последовательности АР-параметров;

3) в виде конечной последовательности коэффициентов отражения.

Коэффициентами отражения называют коэффициенты km=amf(m), 1£m£p фильтра линейного предсказания (ЛП) вперед.

Оценка и ошибка линейного предсказания вперед:

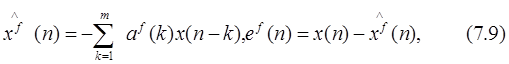
где ЛП вперед понимается в том смысле, что результат предсказания для текущего отсчета данных является взвешенной суммой из p предшествующих отсчетов.

Оценка и ошибка ЛП назад:

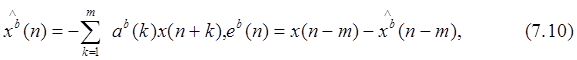
где ЛП назад понимается в том смысле, что результат предсказания для текущего отсчета данных являтся взвешенной суммой из p последующих отсчетов.

Коэффициенты kmявляются параметрами на каждой ступени решетчатого фильтра ЛП ошибки и интерпретируются как физические параметры акустической трубы, используемой в модели речи, или слоистых моделей Земли при обработке сейсмических данных. В структуре решетчатых фильтров одновременно распространяются ошибки ЛП вперед и назад, взаимно ортогональные на каждой ступени фильтра. Решетчатый фильтр мало чувствителен к шуму округления и флуктуациям значений коэффициентов.

Для того, чтобы все три отображения АР-процесса были возможны, необходимо, чтобы выполнялись следующие три эквивалентных условия:

1) rxx(0),..., rxx(p) являлась положительно-определенной АКП;

2) полином

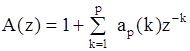являлся минимально-фазовым полиномом;

3) модуль коэффициента отражения ½km½<1 и дисперсия на m-й ступени s2m>0, 1£m£p.

Соответствующие этим представлениям методы оценки параметров представлены на рис. 7.3. В отдельную группу выделены методы, основанные на линейном предсказании по методу наименьших квадратов.

Рис.7.3

Рис.7.4

Если анализируется процесс x(t)=m(t)+n(t), где n(t) - стационарный случайный процесс со спектром, ширина которого значительно превышает ширину спектра детерминированной функции m(t), то фунция m(t) характеризует отклонение процесса x(t) от стационарности и называется трендом.

Блок-схема блочных алгоритмов АР-оценивания СПМ приведена на рис. 7.4.

7.3. Оценка параметров АР-моделей по автокореляционной

последовательности. Метод Юла-Уолкера

АР-модель описывается уравнением (7.6):

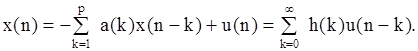
Умножая обе его части на x*(n-m) и усредняя (операция < >), получим

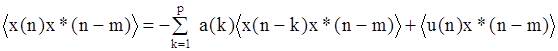или

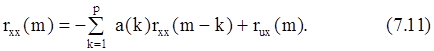
Взаимную корреляцию rux(m) найдем из второго равенства (7.6):

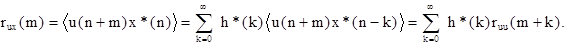
Т.к. u(n) - белый шум, то

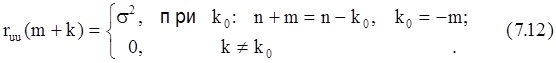
При m>0 k0<0, h(k0)=0 и rux(m)=0;

при m£0 k0³0, h(k0)=h*(-m) и rux(m)=s2h*(-m).

АКП при m<0 по определению rxx(m)=rxx*(-m). Подставляя значения rux(m) в (7.11), получим

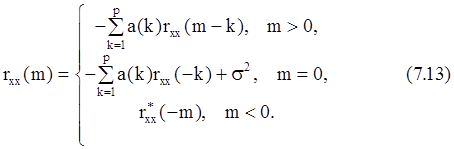Это выражение можно записать для p+1 значений индекса временного сдвига 0£m£p в матричной форме

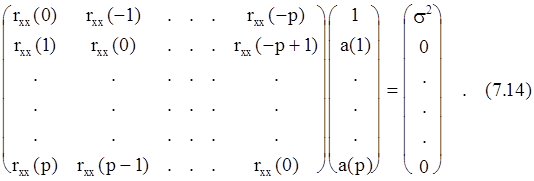
Таким образом, если задана АКП для 0£m£p, то АР-параметры можно найти в результате решения уравнений (7.14), которые называются уравнениями Юла-Yолкера для АР-процесса.

Процедура оценивания СПМ по АР-параметрам, получающимся в результате решения уравнений (7.14), называется алгоритмом Юла-Уолкера. Если задана последовательность данных, то в уравнения (7.14) вместо значений неизвестной автокорреляционной функции подставляются их оценки, смещенные или несмещенные. Гарантию устойчивости АР-фильтра дает использование смещенных автокорреляционных оценок.

Для решения системы (7.14) можно воспользоваться алгоритмом Левинсона [1, с. 189]. Количество необходимых для этого вычислительных операций пропорционально величине p2.

СПМ АР-процесса получается следующим образом:

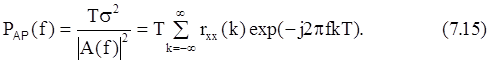
Заметим, что значения автокорреляции, соответствующие значениям индекса временного сдвига от 0 до p, однозначно описывают АР(p)-процесс, т. к. значения автокорреляции при ½k½>p получаются рекурсивно (см. формулу (7.13)).

7.4. Оценка параметров АР-моделей по последовательности оценок

коэффициентов отражения

Рекурсивное решение уравнений Юла-Уолкера методом Левинсона связывает АР-параметры порядка p с параметрами порядка p-1 выражениями [1, с. 239]

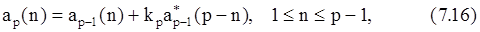
а коэффициент отражения определяется по известным значениям АКФ, соответствующим корреляционным сдвигам от 0 до p-1:

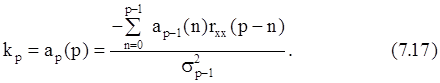
Рекурсивное выражение для дисперсии возбуждающего белого шума:

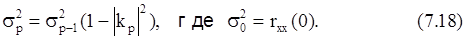
Одна из процедур получения АР-оценки СПМ в том случае, когда имеется некоторый блок отсчетов данных, может быть основана на оценивании коэффициента отражения по этим отсчетам на каждом шаге рекурсии Левинсона. Эта идея реализована в трех следующих методах.

7.4.1. Геометрический алгоритм

Ошибки ЛП вперед и назад определяются соответственно выражениями

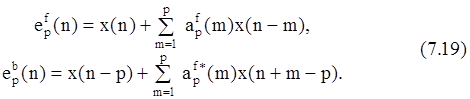Подставляя сюда значение ap(n) из (7.16), получаем рекурсивные соотношения

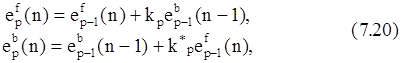
которые связывают ошибки предсказания порядка p с ошибками предсказания порядка p-1.

Коэффициент отражения можно рассматривать как взятый со знаком минус нормированный коэффициент корреляции между ошибками ЛП вперед и назад с единичным временным сдвигом [1, с. 241]:

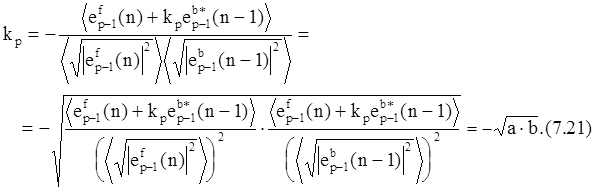
Это выражение определяет геометрическое среднее между нормированной корреляцией ошибки предсказания вперед (а) и нормированной корреляцией ошибки предсказания назад (b). Подставляя в (7.21) оценки взаимной корреляции и автокорреляции ошибок предсказания вперед и назад

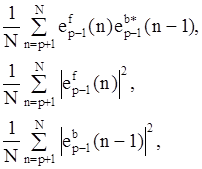
получим оценку коэффициентов отражения:

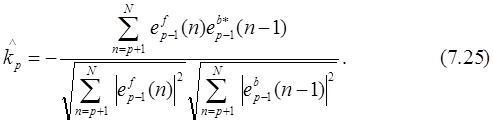
Заметим, что т. к. масштабирующий множитель 1/N сократился, то не имеет значения, используются смещенные или несмещенные оценки корреляции. Индексы ошибок предсказания лежат в диапазоне от n=p+1 до n=N, т. к. используются только имеющиеся отсчеты данных. Можно показать, что ½kp½£1, что гарантирует устойчивость АР-фильтра.

Алгоритм вычислений таков.

Оценки коэффициентов отражения находятся по формуле (7.22) с использованием рекурсий для ошибок предсказания (7.20), начиная с рекурсии нулевого порядка

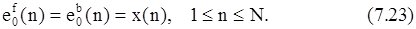
В качестве начального значения дисперсии ошибки ЛП используется оценка

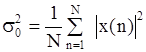
- мощность, содержащаяся в N отсчетах данных. Параметры модели находятся по оценкам коэффициентов отражения с помощью формул (7.16).

7.4.2. Гармонический алгоритм Берга

Один из самых первых и наиболее известных алгоритмов АР спектрального оценивания был предложен Дж. Бергом. Алгоритм Берга отличается от геометрического алгоритма лишь последним этапом: в нем используется другой тип оценки коэффициента отражения - оценка, определяемая по методу наименьших квадратов. При каждом значении p в нем минимизируется арифметическое среднее мощности ошибок ЛП вперед и назад (7.20) (выборочных дисперсий ошибок предсказания)

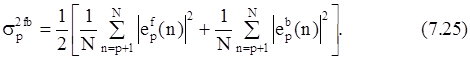
Суммирование ведется только по имеющимся отсчетам данных. Величина spfb является функцией только комплексного коэффициента отражения kp, т. к. ошибки предсказания, начиная с порядка p-1, известны.

Найдем минимум sp2fb, приравнивая комплексную производную от нее нулю:

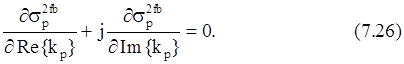
Решая это уравнение относительно kp, получим оценку по МНК

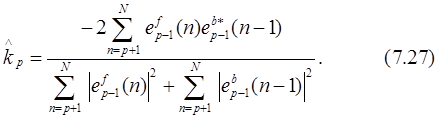
Эта оценка представляет собой гармоническое среднее (2ab/(a+b)) коэффициентов нормированной корреляции ошибок предсказания вперед (а) и назад (b). Модуль ½kp½£1, и АР-фильтр будет устойчив.

Н. Андерсен предложил следующее рекурсивное выражение, которое упрощает вычисление знаменателя (denominator, DEN) (7.27):

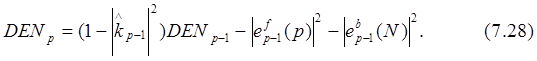
Реализация алгоритма Берга требует выполнения 3Np-p2комплексных сложений и умножений и p действительных делений плюс память для хранения 3N+p комплексных чисел.

Для уменьшения смещения оценки частоты был предложен ряд модификаций метода Берга, взвешивающих средний квадрат ошибки предсказания

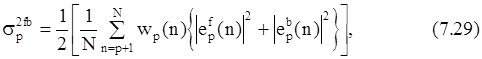
что дает оценку коэффициента отражения

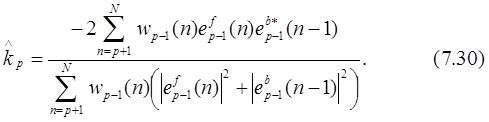
В алгоритме Берга использовалась равномерная весовая функция
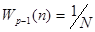. Д. Суинглер предложил использовать окно Хэмминга, М. Кавех и Дж. Липперт - специальное квадратичное окно, Б. Хелме и К. Никиас - адаптивную к данным весовую функцию вида

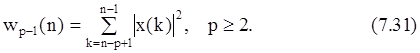
7.4.3. Рекурсивное оценивание по методу максимального

правдоподобия

Алгоритм для действительных данных разработан С. Кеем. В нем для получения коэффициентов отражения и обновления порядка АР-коэффициентов, получаемых с помощью рекурсии Левинсона, используется метод максимального правдоподобия.

Если плотность вероятности гауссовского АР-процесса с нулевым средним максимизируется относительно коэффициента отражения kpи дисперсии возбуждающего шума sp2в предположении, что АР-коэффициенты порядка p-1 уже вычислены, то оценки kpи sp2, максимизирующие эту плотность вероятности для заданной последовательности данных {x(0), x(1),..., x(N-1)}, получаются как решения кубического уравнения

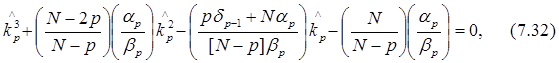
для которого определяется его действительный корень на интервале [-1,1], и линейных уравнений

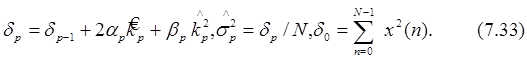
Действительные коэффициенты ap и bp определяются с помощью квадратичных форм

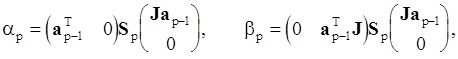
где a T=(1 ap-1(1)... ap-1(p-1))T- вектор авторегрессионных коэффициентов;

J - (pxp)-матрица отражения;

S p- (p+1)x(p+1)-матрица с элементами, определенными при 0£i,j£p:

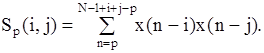
Алгоритм запускается вычислением d0. Найденные из (7.33) оценки Kpподставляются в рекурсию Левинсона (7.16) для определения АР-параметров.

7.5. Оценка параметров АР-моделей, основанная на линейном

предсказании по МНК

Налагая на АР-коэффициенты ограничения (их взаимосвязь по рекурсии Левинсона), Берг оптимизировал по МНК единственный параметр - коэффициента отражения. Отбросив данное ограничение, можно оптимизировать по МНК одновременно все коэффициенты ЛП.

Существует два типа алгоритмов спектрального оценивания по МНК.

1) Алгоритмы с раздельными оценками коэффициентов ЛП вперед и назад.

Предположим, что для оценивания АР-параметров порядка p имеется N-точечная последовательность данных {x(1),..., x(N)}. Ошибка ЛП вперед дается выражением

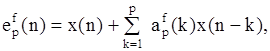
где epf(n) не является белым шумом, т. к. последовательность данных конечна. Поэтому, чтобы воспользоваться АР-моделью, будем полагать, что ошибка предсказания является отбеленным процессом, что позволит приравнять АР-параметры и коэффициенты ЛП.

Ошибку ЛП вперед можно определить в диапазоне временных индексов от n=1 до n=N+p, если предположить, что данные до первого и после последнего отсчетов равны нулю (x(n)=0 при n<1 и n>N).

Необходимо минимизировать модуль среднего квадрата ошибки ЛП

или sp2f/N - выборочную дисперсию.

Рассмотрим три случая спектрального оценивания.

а) Выбирая полный диапазон суммирования от epf(1) до epf(N+p), получаем так называемый взвешенный случай, т. к. он включает пред- и постобработку данных c помощью окна (приравнивание отсутствующих данных к нулю). Этот случай получил название автокорреляционного метода ЛП. Метод эквивалентен методу Юла-Уолкера для оценивания АР-параметров по смещенным корреляционным оценкам. Обработка данных с помощью окна ухудшает разрешение, поэтому в случае коротких записей данных метод редко применяется на практике.

б) Выбирая диапазон суммирования от epf(1) до epf(N), получаем предвзвешенный случай, т. к. полагается, что значения данных, предшествующих отсчету x(1), равны нулю. Метод предвзвешивания целесообразно использовать в процедурах ЛП по МНК, основанных на последовательной обработке данных.

в) Диапазон суммирования от epf(p+1) до epf(N) соответствует невзвешенному случаю, т. к. используются только имеющиеся отсчеты данных. Метод называется ковариационным. Для этого метода существенно ограничение: выбранный порядок модели не должен превышать половины записи данных: p£N/2. В случае гауссовских процессов ковариационный метод дает для АР-параметров оценку, приближающуюся к оценке максимального правдоподобия. Вычислительные затраты пропорциональны величине p2.

Все три метода могут быть рассмотрены и применительно к оценке ЛП назад.

Следует отметить, что коэффициенты ЛП вперед и назад, определяемые с помощью ковариационного метода, не гарантируют получение устойчивого фильтра. В задаче спектрального оценивания это не приводит к каким-либо затруднениям. Более того, спектральные оценки, получемые по оценкам АР-коэффициентов, определяемых с помощью ковариационного метода, обычно имеют меньшие искажения, чем спектральные оценки, получаемые с помощью методов, гарантирующих устойчивость фильтра ЛП, например, с помощью автокорреляционного метода.

В одном из вариантов ковариационного метода (К. Никиас и П. Скотт) коэффициенты ЛП вперед и назад выбираются на основе взвешенных квадратов ошибок

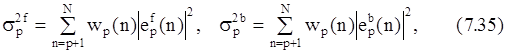
где веса характеризуют энергию отсчетов данных, используемых для формирования ошибок предсказания в пределах окна

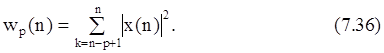
2) Комбинированные алгоритмы ЛП вперед и назад.

Поскольку оба направления предсказания обеспечивают получение одинаковой статистической информации, целесообразно объединить статистики ошибок ЛП вперед и назад, чтобы получить большее число точек, в которых определяются ошибки.

Минимизируется среднее значение квадратов ошибок предсказания вперед и назад

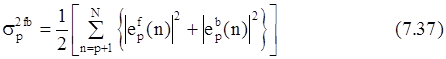
по имеющимся данным. Т. к. диапазон суммирования идентичен диапазону суммирования в ковариационном методе, то метод получил название модифицированного ковариационного метода. Метод был независимо разработан Бергом, Ульрихом, Клейтоном и Наттолом. Значение выбранного порядка модели не должно превышать двух третей длины записи данных: p£2N/3.

В отличие от метода Берга, модифицированный ковариационный метод не гарантирует получение устойчивого фильтра ЛП. Но модули коэффициентов отражения всегда не превосходят 1, поэтому мы будем получать устойчивые решетчатые фильтры.

7.6. Сравнительные характеристики СПМ, получаемых с помощью

блочных методов АР-оценивания

Если выбран большой порядок АР-модели относительно имеющегося числа отсчетов данных, то дополнительные полюсы, порожденные лишними АР-параметрами, приводят к появлению ложных спектральных пиков. Уменьшение же порядка модели снижает разрешение спектральной оценки. При заданном порядке модели более высокое разрешение обеспечивают метод Берга, ковариационный и модифицированный ковариационный методы. Это связано с отсутствием в них использования окон (существенного момента всех классических методов, см. главу 5) и всех сопутствующих им эффектов. Если в методах с использованием окна за пределами этого окна применяется нулевая, то в методе Берга и др. - ненулевая экстраполяция АКП, определяемая выражением

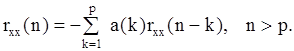
Это иллюстрируется рисунком 7.5.

Рис. 7.5. Экстраполяция автокорреляционной последовательности: а - исходная бесконечная АКП и истинный спектр процесса, состоящего из одной синусоиды в белом шуме; б - экстраполяция в коррелограммном методе; в - экстраполяция при АР-оценивании СПМ.

При использовании метода геометрического среднего, метода Берга и автокорреляционного метода может возникать расщепление спектральных линий (рис. 7.6). Фужер, впервые описавший это явление, отмечал, что при использовании метода Берга расщепление спектральных линий наиболее вероятно в тех слуях, когда

1) велико отношение сигнал/шум;

2) начальные фазы синусоидальных компонент нечетно кратны углу 45 градусов;

Дата добавления: 2015-05-09