Использование окон в спектральном анализе 2 страница

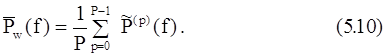
Множитель 1/U в (5.9) устраняет эффект влияния энергии окна на смещение в оценке СПМ PW(f). Можно показать (доказать это утверждение студентам предоставляется самостоятельно), что смещение периодограммы Уэлча представимо в следующем ви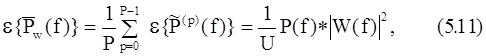де:

где

– дискретно-временное преобразование Фурье окна данных, а P(f) - истинная СПМ.

ОДВПФ функции (5.11) дает ожидаемое значение эффективной автокорреляционной после­довательности периодограмм Уэлча

– автокорреляционная последовательность окна данных.

Полная мощность в исходной последовательности отсчетов данных определяется членом автокорреляционной последовательности, соот­ветствующим нулевому временному сдвигу. Поскольку U=Ф(0), то

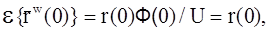
a это означает, что rW(0) - несмещенная оценка мощности.

До сих пор мы оценивали автоспектральную плотность, причем в обозначениях СПМ были опущены подстрочечные индексы xx. Процедура Уэлча для оценивания взаимной спектральной плотности во многом аналогична процедуре оценки спектральной плотности. В этом случае N-точечные последовательности x(n) и y(n) сначала сегментируются и взвешиваются, в результате чего получаются последовательности

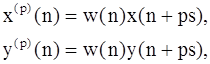
где 0£n£D-1, 0£p£P-1, по которым затем вычисляется выборочный взаимный спектр

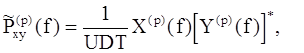где

– ДВПФ, а U – энергия дискретно-временного окна. Усреднение по периодограммам всех сегментов дает окончательную оценку периодограммы

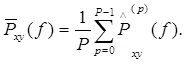
В случае гауссовских процессов характеристики среднего значения и дисперсии этой взаимной спектральной оценки во многом сходны с характеристиками аналогичных величин для cпектральной оценки.

Уэлч, в частности, предложил использовать окно Ханна и 50%-ное перекрытие сегментов, которое обеспечивало очень эффективные реализации его метода на основе алгоритма БПФ при вычислении оценки (5.10) на некоторой сетке частот. Кроме того, при 50%-ном пе­рекрытии сегментов все данные используются дважды, за исключением D/2 отсчетов на каждом конце исходной N-точечной последовательно­сти данных, а это выравнивает обработку большинства отсчетов дан­ных, поскольку те отсчеты, которые имеют малые веса на одном сег­менте, получают большие веса на следующем сегменте. Анализ поведе­ния дисперсии периодограммы Уэлча для гауссовских процессов пока­зал, что минимальная дисперсия для окна Ханна достигается при 65%-ном перекрытии, при этом величина дисперсии увеличивается прибли­зительно на 8% при использовании 50%-ного перекрытия сегментов. Так же как и дисперсия периодограммы Бартлетта, дисперсия перио­дограммы Уэлча примерно обратно пропорциональна числу сегментов, т. е.

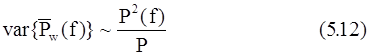
в предположении независимости сегментов (хотя перекрытие сегментов приводит, конечно, к некоторой их зависимости). Благодаря перекры­тию сегментов при одинаковой длине исходной последовательности данных, можно сформировать большее число сегментов, чем в методе Бартлетта, а это уменьшает величину дисперсии периодограммы Уэлча по сравнению с дисперсией периодограммы Бартлетта.

В ряде опубликованных исследований утверждается, что примене­ние окон данных лишь придает одним отсчетам большую значимость пе­ред другими отсчетами, а также ухудшает разрешение (уширяет глав­ный лепесток частотного окна) без какого-либо компенсирующего уменьшения дисперсии. Эти утверждения, несомненно, верны в отноше­нии выборочного спектра, получаемого сразу по всей последователь­ности отсчетов сигнала с относительно плоской спектральной харак­теристикой. Однако по отношению к периодограмме Уэлча они не верны, поскольку перекрытие сегментов как раз и используется для выравнивания обработки (т. е. выравнивания значимости отсчетов) данных, а увеличение числа сегментов - для уменьшения дисперсии оценки СПМ. Не верны они и в отношении спектров сигналов с большим различием амплитуд составляющих.

Рис.5.2

Рассмотренные периодограммные методы анализа отображены на рис. 5.2. Следует заметить, что при выборе того или иного метода необходимо учитывать его ограничения и особенности. Так, очевидно, метод Даньелла неприменим при значительных флуктуациях P(f). Однако, по-видимому, ему следует отдать предпочтение, если априорно известно, что P(f)=const в диапазоне анализа. В этом случае выражение (5.3) представимо в виде

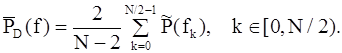
Сегментирование исходной последовательности x(n), используемое в методах Бартлетта и Уэлча, приводит к ухудшению разрешающей способности в P раз, поэтому при выборе числа элементов в сегменте также необходимо иметь априорную информацию о спектре флуктуаций P(f) в диапазоне анализа.

5.2. Корреляционный анализ и спектральная оценка

Одной из важнейших временных характеристик сигнала является автокорреляционная функция (АКФ), позволяющая судить о степени связи сигнала с его сдвинутой по времени копией. Для действительной последовательности х(n) АКФ определяется в единицах мощности:

При m=0 значение АКФ достигает максимума и равно средней мощности сигнала х(n):

Для оценки степени подобия двух сигналов х(n) и y(n) используется функция взаимной корреляции (ФВК):

При m=0 значение ФВК определяет взаимную мощность сигналов х(n) и y(n):

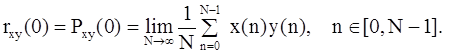
Функцию взаимной корреляции измеряют в случаях, когда последовательности х(n) и y(n) связаны операциями фильтрации и задержки. Например, в радиолокационных системах y(n) - это отфильтрованный, зашумленный и задержанный зондирующий сигнал х(n). В таких случаях положение максимума ФВК дает величину задержки входного сигнала, что является основой для решения многих задач радиолокации. Пусть, например, {х(n)}=(0,1,3,6,2,1,0,0) и y(n) сдвинута на два отсчета: {y(n)}=(3,6,2,1,0,0). Найдем ФВК: {z(m)}=(18/6, 36/6, 50/6, 32/6, 12/6, 3/6). Анализируя ФВК, находим ее максимум: z(2)=50/6. Номер (m=2) максимума соответствует сдвигу y(n) относительно х(n). На рис. 5.3 представлен пример двух сдвинутых на 28 отсчетов последовательностей и их функция взаимной корреляции.

Рис. 5.3

Спектральная плотность АКФ равна спектральной плотности мощности [6, с. 77]. Таким образом, спектральная плотность мощности (СПМ) определяется как ДВПФ автокорреляционной последовательности:

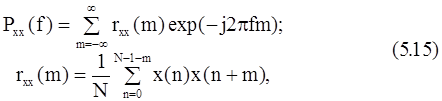
где rxx(m) - функция автокорреляции, а N - число выборок x(n), 0£n£N-1.

Взаимная СПМ двух процессов х(n) и y(n) определяется как ДВПФ взаимной корреляционной последовательности:

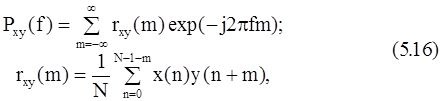
где rxy(m) - функция взаимной корреляции, а N - число выборок х(n) и y(n).

Функция СПМ описывает распределение мощности случайного процесса по частоте. В силу того, что функции АКФ и ВКФ имеют конечную длину, то бесконечные пределы суммирования заменяют на конечные. Если принять во внимание, что х(n) и y(n) имеют большое число выборок (N®¥), то основная формула для вычислений АКФ и ФВК:

Предельные выражения показывают, что средние значения оценок сходятся при больших N к некоторому определенному постоянному числу. Формулы (5.17) и (5.18) хорошо работают при N>1024. Однако дисперсия оценки Pxx(f) и Pxy(f) будет сходится к нулю лишь при выполнении дальнейшего усреднения этих оценок.

Рассмотрим более подробно

1) метод получения оценки функции корреляции;

2) метод получения статистически устойчивых оценок СПМ на основе функции корреляции, получивший название корреляционного или коррелограмного метода оценки СПМ.

5.2.1. Метод получения оценки ФВК

Рассмотрим последовательности х(n) и y(n). Их ДПФ:

Умножение X(k)Y(k) соответствует свертке х(n) и y(n):

Таким образом, ФВК можно найти как ОДПФ от произведения ДПФ исходных последовательностей:

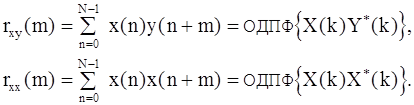
Причем х(n) и y(n) во всех выкладках считаются действительными.

Алгоритм получения оценки АКФ и ФВК опирается на метод быстрой свертки и для последовательностей х(n) и y(n) (0£n£N-1) выглядит следующим образом:

1) Вычислить x'(n)=x(n)w(n),

y'(n)=y(n)w(n).

2) Вычислить X(k)=БПФ{x'(n)},

Y(k)=БПФ{y'(n)}.

3) Вычислить оценку Sxy(k)=X(k)Y*(k).

4) Получить оценку ВКФ, выполнив rxy(m)=ОБПФ{Sxy(k)}.

Схема алгоритма изображена на рис. 5.4.

Рис. 5.4

В этом методе алгоритм БПФ используется непосредственно для вычисления спектральной плотности мощности Sxy(k) на L дискретных частотах. Для уменьшения эффектов просачивания каждая из последовательностей умножается на сглаживающее окно w(n). После выполнения ОБПФ имеем искомую ФВК.

5.2.2. Коррелограммный метод оценки СПМ

Суть алгоритма коррелограмного метода оценки СПМ заключается в усреднении функции корреляции. Вся реализация x(n) длиной N разбивается на M кусков с перекрытием. Для каждого куска вычисляется своя АКФ ri(m), далее производят суммирование по всем iÎ[1,M]:

Оценку СПМ определяют как ДПФ от rxx(m):

Для того, чтобы дисперсия оценки сходилась к нулю, необходимо выполнение соотношения L<<N. В результате оценка СПМ вычисляется через преобразование последовательности, усеченной во временной области. Усечение во временной области может вызвать большие пульсации в частотной области, для их подавления используются окна. На выбор окна накладываются некоторые ограничения. Если ДПФ окна не является положительной функцией, то возможно, что СПМ будет отрицательной, что лишено физического смысла. Существуют окна, ДПФ которых положительно на всех частотах, например, треугольные окна, симметричные относительно начальной точки отсчета. Если корреляционная последовательность определена на бесконечном интервале временных сдвигов, то окно следует определять симметричным относительно нулевого сдвига; если же - на положительной полуоси, то и окно определяется на этой полуоси.

Схема алгоритма коррелограммного метода приведена на рис. 5.5.

Рис. 5.5

Для корреляционного метода оценки СПМ были разработаны быстрые алгоритмы с применением БПФ. Рассмотрим первый алгоритм. Пусть имеется N-точечная последовательность x(n) (N=20) и необходимо найти первые L отсчетов АКФ (L=5). {x(n)}={x0,x1,x2,x3,x4,...,x17,x18,x19).

Алгоритм выглядит следующим образом:

1. Вычислить U0(k)=ДПФ{x0, x1, x2, x3, x4, x5, x6, x7, x8},

V0(k)=ДПФ{x0, x1, x2, x3, x4, 0, 0, 0, 0},

U1(k)=ДПФ{x5, x6, x7, x8, x9, x10, x11, x12, x13},

V1(k)=ДПФ{x5, x6, x7, x8, x9, 0, 0, 0, 0 },

U2(k)=ДПФ{x10, x11, x12, x13, x14, x15, x16, x17, x18},

V2(k)=ДПФ{x10, x11, x12, x13, x14, 0, 0, 0, 0 },

U3(k)=ДПФ{x15, x16, x17, x18, x19, 0, 0, 0, 0},

V3(k)=ДПФ{x15, x16, x17, x18, x19, 0, 0, 0, 0}.

2. Вычислить Xi(k)=Ui(k)V*(i), iÎ[0,3].

3. Вычислить X(k)=X0(k)+X1(k)+X2(k)+X3(k).

4. Вычислить r(m)=ОДПФ{X(k)}.

Первые 5 отсчетов будут искомым результатом. Из описанной методики видно, что ДПФ должно приблизительно в два раза превышать требуемое число отсчетов корреляционной функции. А требуемое число преобразований ДПФ равно 2К+1, где К=N/L (N - общее число отсчетов сигнала, а L - требуемое количество отсчетов функции корреляции). Затем, дополнив r(m) нулями и выполнив ДПФ, получим оценку СПМ с любым частотным разрешением.

Второй алгоритм эффективнее первого за счет того, что значение Ui(k) можно выразить через Vi(k) и Vi+1(k), но необходимо, чтобы интервал разбиения содержал четное число отсчетов, желательно кратное 2 и прекрытие интервалов было в точности равно 2:1. Для демонстрации алгоритма возьмем ту же последовательность: N=20.

1) Вычислить все Vi(k), где

V0(k)=ДПФ{x0, x1, x2, x3, 0, 0, 0, 0},

V1(k)=ДПФ{x4, x5, x6, x7, 0, 0, 0, 0},

V2(k)=ДПФ{x8, x9, x10, x11, 0, 0, 0, 0},

V3(k)=ДПФ{x12, x13, x14, x15, 0, 0, 0, 0},

V4(k)=ДПФ{x16, x17, x18, x19, 0, 0, 0, 0}.

2) Вычислить Xi(k)=Vi(k)(V*i(k)+(-1)kVi+1(k), причем X4(k)=V4(k)V4*(k).

3) Вычислить

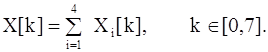
4) Вычислить r(m)=ОДПФ{X(k)}

5) Получить оценку СПМ, выполнив ДПФ от r(m)w(m).

Количество преобразований, которое необходимо выполнить равно К+1, где К - количество интервалов.

В заключение необходимо отметить, что в быстром алгоритме корреляционного метода применяют БПФ, причем необходимую длину последовательности получают дополнением ее нулями.

С увеличением числа значений автокорреляци корреляционный метод дает асимптотически несмещеные оценки СПМ. Блэкман и Тьюки рекомендовали использовать такое число значений оценки автокорреляций, чтобы стандартное отклонение оценки СПМ не превышало 1/3 ее среднего значения, т. е. число оцениваемых значений АКП должно быть равно примерно 10 процентам числа имеющихся отсчетов данных.

Для того, чтобы свести смещение оценок взаимной СПМ к минимуму, следует совместить ВКП и корреляционное окно так, чтобы пики взаимной корреляции соответствовали точке нулевого временного сдвига. Тогда статистические характеристики оценки взаимной СПМ будут аналогичны статистическим характеристикам автоспектральной оценки.

5.3. Критерии качества классической спектральной оценки

Статистический показатель качества оценки определяется как отношение дисперсии оценки СПМ к квадрату математического ожидания этой оценки

Показатель качества Q - это, по сути дела, инвертированное отношение сигнал/шум, которое непосредственно связано со статистической устойчивостью спектральной оценки. Значения Q, много меньшие единицы, соответствуют гладким спектральным оценкам с малыми флуктуациями (малой дисперсией). Зачения Q, много большие единицы, соответстуют весьма зашумленным спектральным оценкам с большой дисперсией.

Существует очень важное соотношение между следующими величинами.

Bs- эффективная статистическая ширина полосы, характеризует ширину полосы эквивалентного прямоугольного окна с тем же значением отношения дисперсии к квадрату среднего значения на его выходе, как и у используемого окна W(f) в том случае, когда на вход подан белый шумовой процесс, и равна

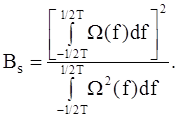
Полоса Bs связана с эквивалентной детерминированной шириной полосы Весоотношением Bs=aBe, где коэффициент а равен примерно 0.8 для прямоугольного окна, 1.3 для окна Ханна и 1.4 для окна Хэмминга.

Те=NT секунд - длительнсть временного сигнала.

Если значение произведения TeBsвыбрано значительно большим единицы, то для всех классических спектральных оценок будет выполняться соотношение

Произведение "устойчивость´длительность´ширина полосы" устанавливает взаимосвязь между тремя фундаментальными параметрами, от которых зависят характеристики спектральных оценок. Для данной записи данных продолжительностью Теневозможно получить оценки, которые одновременно обладают высоким разрешением (малыми значениями Bs) и высокой устойчивостью (малыми значениями Q). Заметим, что увеличение числа отсчетов за счет увеличения частоты дискретизации при неизменном интервале Тене будет влиять на максимально достижимое разрешение, так как на него влияет только длина записи данных, но не число отсчетов.

Если неизвестно, как выбирать компромиссное решение относительно устойчивости и разрешения оценок, то рекомендуется начать с выбора максимальной устойчивости, а это значит - с минимального разрешения, а затем постепенно увеличивать длину сегментов (в случае периодограммы) или число корреляционных членов (в случае коррелограммы). Следует продолжать эту процедуру до тех пор, пока достигнутое разрешение не позволит передать наиболее тонкие и важные детали спектра. Если информация о важности деталей отсутствует, то следует остановиться тогда, когда дальнейшее увеличение длины сегментов данных или величины временных сдвигов к существенным изменениям в спектральных оценках уже не приводит.

5.4. Комбинированные периодограммно-коррелограммные оценки

Основной комбинированный метод состоит из четырех этапов.

1) Вычисляется обычная периодограмма Уэлча Pw(f) с произвольным выбором перекрытия сегментов S и окна данных w(n).

2) Вычисляется ОДВПФ для Pw(f) с целью получения симметричной оценки АКФ rxxw(m) для 2D+1 временных сдвигов. Оценка АКФ rxxw(m) охватывает значения ½m½£D вследствие воздействия АКФ окна данных ф(m)=w(n)*w(n).

3) Эта оценка обрабатывается с помощью действительного симметричного корреляционного окна w(m) нечетной длины 2L+1 и получается взвешенная оценка АКФ:

Ширина этого корреляционного окна выбирается меньше ширины автокорреляционной функции Ф(m) окна данных (L<D).

4) Вычисляется ДВПФ для rxxс(m), что и дает искомую оценку СПМ:

где W(f) - преобразование Фурье корреляционного окна w(m).

Комбинированное временное и корреляционное взвешивание позволяют управлять уровнем боковых лепестков. Устойчивость оценки обеспечивается за счет усреднения по сегментам и частотного сглаживания (корреляционного взвешивания).

Среднее значение оценки СПМ

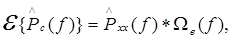
где We(f) - преобразование Фурье эффективного корреляционнного окна we(m):

Если эффективное корреляционное окно выбрано заранее, тогда при L<D окно данных можно выбирать произвольно, т. к. его влияние может быть скомпенсировано выбором корреляционного окна следующего вида:

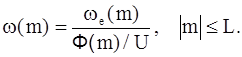
Чтобы оценка 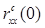была несмещенной оценкой полной мощности, нормируют корреляционные окна так, чтобы we(0)=1, w(0)=1.

Для получения с помощью этого метода оценки Блэкмана-Тьюки (крайний коррелограммный частный случай) используем один сегмент (P=1), корреляционное окно шириной много меньше числа отсчетов данных (L<<D=N), и прямоугольное окно данных (w(n)=1, n=0,..., N-1). Наттол показал, что в этом случае QteBs>>1.

Для получения периодограммы Уэлча (крайний периодограммный частный случай) используем P=2N/D-1 сегментов, 62-процентное перекрытие (S=0,38D), окно Ханна данных и не применяем корреляционного взвешивания (w(m)=1, ½m½£L=D). И в этом случае QteBs>>1. При использовании 50-процентного перекрытия QteBs>>1,08.

Очень интересен частный случай, называемый методом Наттола-Картера, использующий прямоугольное окно данных (w(n)=1) без перекрытия (S=D), число сегментов, вдвое меньшее, чем для периодограммы Уэлча, и корреляционное окно, подбираемое для получения эффективного корреляционного окна Ханна. Здесь QteBs>>1, метод имеет те же статистические характеристики, что и метод Уэлча. Однако вычислительные затраты для него вдвое ниже, чем для метода Уэлча, т. к. БПФ в нем вычисляется для вдвое меньшего числа сегментов, к тому же в нем отсутствуют операции умножения, связанные с обработкой сегментов с помощью окна данных.

Дата добавления: 2015-05-09