Соотношения между БПФ и цифровой фильтрацией 2 страница

Здесь fm(i) и fm(j) - входные числа базовой операции, fm+1(i) и fm+1(j) - выходные числа, Wp- поворотный множитель. Очевидно, что при переходе от этапа к этапу модули чисел, вообще говоря, увеличиваются и удовлетворяют неравенству

Следовательно, уровень сигнала на каждом этапе увеличивается не более, чем в 2 раза, т. е. не быстрее, чем на один двоичный разряд. Единственный способ бороться с этим - масштабировать числа (т. е. умножать их на какое-либо число, меньшее единицы).

Учитывая вышеизложенное, можно предложить три метода масштабирования:

1) Сдвиг вправо на один разряд на каждом этапе (это эквивалентно делению чисел на два). Если модуль f0(i) не превышает 0.5 для любых i и числа сдвигаются вправо на один разряд после каждого этапа, кроме последнего, то переполнения не будет.

2) Контроль последовательности, гарантирующий выполнение условия fm(i)£1/2 для всех i. На каждом этапе БПФ вычисляется массив fm(i) и, если хотя бы один отсчет массива превысит по модулю 0.5, весь массив масштабируется сдвигом вправо на один разряд.

3) Проверка на переполнение. Исходная последовательность масштабируется так, чтобы модули действительной и мнимой частей f0(i) были меньше 1 (а не 0.5, как в предыдущих методах). Если в ходе выполнения базовой операции фиксируется переполнение, то все числа последовательности, включая результаты уже выполненных на данном этапе (без переполнения) базовых операций, сдвигаются на один разряд вправо, после чего итерация продолжается с той базовой операции, где произошло переполнение. На каждом этапе может произойти более одного переполнения, но не более двух.

Первый метод связан с наименьшими затратами времени и наиболее прост для практической реализации. Однако, он дает наименьшую точность, т. к. масштабирование на каждом этапе приводит к ненужному ухудшению точности в случаях, когда его можно не производить. Второй метод требует больших затрат времени (поскольку на каждом этапе приходится вычислять модули всех чисел массива), и в то же время он не слишком точный, т. к. модули всех элементов массива не превышают 0.5 и, как следствие, один разряд памяти данных не используется. Третий метод является самым точным, но и самым медленным, т. к. приходится повторно обрабатывать всю последовательность всякий раз, когда обнаруживается переполнение.

Уэлч разработал довольно простую методику расчета граничных значений уровня шума округления, возникающего при БПФ. Наличие шума округления обусловлено двумя факторами:

1) Появлением погрешности при округлении произвдения Wpfm(j). Если Wpи fm(j) представлены b-разрядными числами (т. е. действительная и мнимая части Wpи fm(j) содержат по b разрядов, то после округления каждого из четырех действительных произведений, входящих в Wp*fm(j), до b-разрядного числа получается ошибка, равномерно распределенная на интервале [-2-b/2, 2-b/2] и имеющая нулевое среднее и дисперсию 2-2b/12.

2) Сдвигом суммы на один разряд вправо, если при сложении происходит переполнение. Если младший разряд, при сдвиге выходящий за пределы регистра, равен нулю, то ошибки не будет. Если же он равен единице, то в зависимости от знака числа возникает ошибка величиной ±2-b. Дисперсия этой ошибки равна 2-2b/2.

Верхнюю границу отношения дисперсии шума округления к дисперсии выходных гармоник можно получить, предположив, что переполнение происходит на каждом этапе, так что числа каждый раз приходится масштабировать. Если fk(j) - отсчеты, получаемые на k-м этапе, то D(fk) - их дисперсия, определяемая как

причем

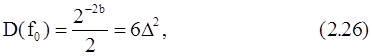
где D2=2-2b/12. Равенство (2.26) получается в предположении, что на первом же этапе может произойти переполнение, поэтому в числах нулевого этапа (т. е. в исходных отсчетах) один младший разряд отбрасывается. Базовая операция первого этапа содержит умножения только на ±1, поэтому шум округления произведений отсутствует.

На втором этапе, согласно предположению, также может произойти переполнение, поэтому массив f1(j) нужно предварительно промасштабировать сдвигом вправо каждого элемента на один разряд. Тогда дисперсия D(f1) будет равна

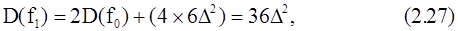
причем множитель 4 отражает тот факт, что ошибка при усечении выходных чисел на первом этапе будет вдвое больше ошибки, обусловленной усечением выходных чисел на нулевом этапе, поэтому дисперсия возрастает в четыре раза.

На втором этапе БПФ с прореживанием по времени выполняются умножения только на ±1 и ±j, поэтому ошибка, связанная с округлением произведений, опять будет равна нулю. Итак, в предположении, что числа f2(j) также масштабируются, получим следующую формулу для дисперсии ошибки на втором этапе БПФ:

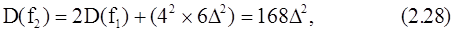
причем множитель 42указывает на удвоение ошибки усечения при переходе от первого этапа ко второму.

На последующих этапах в большинстве базовых операций выполняются нетривиальные умножения. Так, на третьем этапе половина базовых операций содержит такие умножения, на четвертом этапе - три четверти и т. д. Согласно формулам (2.23), общие выражения для действительной и мнимой частей результата базовой операции на m-ом этапе имеют вид:

Для тех базовых операций, где умножение на Wpне является тривиальным, дисперсия результата fm+1(включая шум округления произведений и шум усечения при масштабировании) имеет вид:

где D(emlm+1) - дисперсия шума округления умножения на m-ом этапе, а D(esm+1) - дисперсия шума масштабирования на том же этапе.

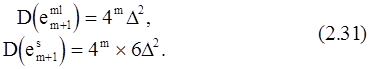
Третье слагаемое формулы (2.30) содержит произведение квадрата модуля Wpи D(fm). Поскольку Wp=1, это слагаемое совпадает с первым членом суммы. Второе слагаемое равно произведению D(Wp) на среднее значение квадарата модуля переменных, преобразуемых на m-ом этапе. Дисперсия Wpравна D2(поскольку Wpпредставляется b-разрядным числом с погрешностью). Чтобы определить среднее квадрата модуля переменных, обрабатываемых на m-м этапе, нужно знать величину К, представляющую собой среднее квадрата модуля исходного массива чисел, равное

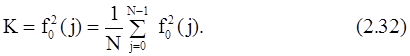
Учитывая, что среднее значение кадрата модуля увеличивается от этапа к этапу вдвое, получим, что на выходе m-го этапа оно будет равно 2mK. Тогда D(fm+1) становится равной

если во всех базовых операциях m-го этапа выполняются нетривиальные умножения. Если же ввести a - долю базовых операций с нетривиальными умножениями (0£a£1), то второе и третье слагаемые суммы (2.33) следует умножить на a. Так, если a=0 (как это имеет место на первом и втором этапах), то равенство (2.33) переходит в (2.27) (при m=0) или в (2.28) (при m=1). Если принять, что a=0.5 на третьем этапе и a=1 на всех последующих этапах, причем номер последнего этапа равен M, то получим

Поскольку среднее значение квадратов модулей элементов выходного массива {fm(j)} равно 2^Mk, то среднее квадрата их действительных (или мнимых) частей равно 2^МК/2. Таким образом, оценкой отношения дисперсии шума к дисперсии сигнала на выходе (в пределе при больших М) является величина

Итак, верхняя граница отношения ошибки к выходному сигналу возрастает как 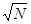, т. е. по 1/2 разряда на этап.

Формулу, аналогичную (2.35), можно получить и для нижней границы отношения ошибок шума и сигнала, если предположить что переполнений вообще не происходит, т. е. ошибки, связанные с масштабированием, отсутствуют. Следовательно, вплоть до третьего этапа эта ошибка вообще не возникает. Дисперсия разультата fMбудет иметь вид:

Таким образом, при большом числе этапов М нижняя граница отношения дисперсий ошибки и сигнала на выходе имеет вид

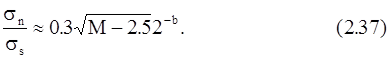
Рассмотренная модель возникновения ошибок была экспериментально подтверждена Уэлчем на многочисленных примерах. Результаты его экспериментов приведены в [2].

В подавляющем большинстве приложений задача измерения спектра сводится к нахождению значений z-преобразования конечной реализации сигнала для большого числа точек, равномерно распределенных по окружности единичного радиуса (рис. 1.4, в).

Пусть анализу подвергается последовательность x(n), положение аргумента которой на временной оси показано на рис. 3.1.

Рис. 3.1

Тогда спектральное измерение сводится к вычислению ДПФ последовательности x(n) и обычно наиболее эффективно выполняется с применением алгоритмов БПФ. С другой стороны, как было показано в главе 1, задача может быть решена с помощью цифровой фильтрации. Там же были приведены схемы, реализующие процедуру скользящего спектрального измерения (спектрального измерения в одной точке z-плоскости). В нашем случае придется повторять ее для каждой из точек z1, z2и т.д. на единичной окружности, в которых оценивается спектр сигнала.

Иногда желательно проводить измерения спектра, вычисляя значения z-преобразования последовательности в равноотстоящих точках, расположенных на окружности радиуса r<1. Задача сводится к предыдущей с помощью предварительного умножения массива сигнала на r-n.

3.1. Некоторые характеристики спектрального анализа на основе БПФ

Двумя наиболее важными характеристиками спектрального анализа являются:

- количество частот, на которых желательно измерить спектр;

- "разрешающая способность" измерения спектра.

Для анализа обеих характеристик лучше всего использовать отмеченную выше эквивалентность между спектральным измерением и фильтрацией.

Чтобы показать, какие факторы влияют на параметры спектрального анализа, рассмотрим пример, представленный на рис. 1.4, г, когда необходимо найти спектр сигнала в 16 точках, равномерно распределенных по единичной окружности. Пусть число L отсчетов сигнала, используемых при измерении спектра, равно 16. Спектральный анализ, удовлетворяющий этому условию, может быть выполнен двумя эквивалентными способами: либо с помощью 16-точечного БПФ, либо с помощью гребенки из 16 фильтров. Импульсная характеристика k-го фильтра, обеспечивающего измерения спектра в точке

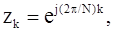равна

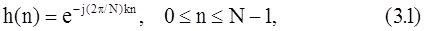
так что ее z-преобразование имеет вид

Вычислив значения H(z) на единичной окружности, получим

Рис. 3.2

На рис. 3.2, а изображены графики функций fN(w,k) для случая, соответствующего рис. 1.4, г, т. е. для 16 точек, равномерно распределенных на единичной окружности. Частотные характеристики фильтров с четными номерами k показаны на рис. 3.2, а вверху, а с нечетными значениями k - внизу. Чтобы избежать путаницы, для всех фильтров, за исключением 8-го, изображены лишь главные лепестки. Видно, что скользящее БПФ эквивалентно довольно грубому набору фильтров с относительно большими боковыми лепестками и существенным перекрытием между соседними фильтрами.

Предположим теперь, что число отсчетов сигнала L больше числа спектральных отсчетов N. Пусть, например, L=32 и N=16. Самый простой способ выполнения таких спектральных измерений состоит в том, что вычисляется 32-точечное скользящее БПФ и просто отбрасываются измерения, соответствующие фильтрам, следующим через один. В результате получится набор фильтров с характеристиками, изображенными на рис. 3.2, б.

Пусть теперь N=16, но имеется только L=8 отсчетов сигнала. В этом случае спектр можно найти, добавив к L отсчетам сигнала N-L нулевых отсчетов так, чтобы общее число преобразуемых отсчетов равнялось количеству спектральных отсчетов, и затем вычислив L-точечное БПФ. Результирующие частотные характеристики фильтров для случая L=8, N=16 приведены на рис. 3.2, в. Число каналов эквивалентной гребенки фильтров осталось прежним, но каждый фильтр стал шире. Таким образом, в рассматриваемом примере главное изменение состоит в ухудшении разрешающей способности по частоте.

Метод выполнения анализа при L=2N становится очевидным, если обратиться к направленному графу БПФ (см., например, рис. 2.9). Видно, что выходные отсчеты с четными номерами располагаются в верхней половине графа. Это означает, что в алгоритме БПФ, предназначенном для получения только четных отсчетов спектра, достаточно лишь частично обработать все L отсчетов, чтобы получить верхнюю половину выходных отсчетов первого этапа БПФ. Как видно из рис. 2.9, только эта половина отсчетов дает все четные коэффициенты ДПФ. Этот подход можно развивать дальше, отметив, например, что восемь верхних выходных коэффициентов дают каждый четвертый коэффициент ДПФ, причем их можно определить, выполнив половину операций на первом этапе, половину - на втором, а также четырехточечное БПФ полученных на втором этапе восьми отсчетов. Пусть в общем случае число отсчетов сигнала L равно MN, где N - требуемое число спектральных отсчетов, а M - целое число, большее единицы. Искомое преобразование равно

Из этой формулы следует, что фактически при вычислении спектра производится предварительное суммирование входных отсчетов, равноотстоящих друг от друга на N точек, после чего вычисляется ДПФ образованной новой последовательности. Смысл этой операции становится понятным, если вспомнить, что дискретизация в частотной области (ее и нужно было получить в данном случае) соответствует наложению во временной области, которое описывается формулой (3.4).

Обратное ДПФ от X(k) даст не исходную последовательность x(n), а набор ее сдвинутых на N отсчетов друг относительно друга копий xi(n), n=0,..., N-1. Пусть L/N=3. Тогда

Из рисунка видно, что неискаженным будет лишь участок n=0,..., N-1. Кроме того, общее число отсчетов увеличилось. Очевидно, что чем ближе значения N к L (М ближе к единице), тем меньше будут искажения, связанные с наложением результатов преобразования.

Из выше приведенных рассуждений следует, что использование последовательностей данных длиной L, большей числа спектральных отсчетов N, улучшает разрешение в N/L раз, но вносит большие искажения и, следовательно, неприменимо в случаях, когда полученная спектральная оценка затем обрабатывается при помощи ОДПФ.

3.2. Соотношение между "скачущим" БПФ и гребенкой фильтров

Выше было показано, что скользящее БПФ в точности эквивалентно анализу с использованием гребенки фильтров, поэтому возникает вопрос, какой из этих двух методов эффективнее с точки зрения объема вычислений. Не вдаваясь в детали, отметим, что при скользящем БПФ для каждого входного отсчета приходится вычислять полное БПФ, т. е. (N/2)log2N базовых операций на отсчет. При анализе с помощью гребенки фильтров, состоящей из гребенчатого фильтра, к выходу которого параллельно подключена группа цифровых резонаторов (рис. 3.3), число комплексных умножений на отсчет равно N. Таким образом, в большинстве случаев, представляющих интерес, гребенка фильтров оказывается эффективнее скользящего БПФ, поскольку в последнем случае не используются возможности итеративного расчета ДПФ. Однако ниже будет показано, что при определенных условиях алгоритм БПФ может оказаться эффективнее эквивалентной ему гребенки фильтров.

Рис. 3.3

Для стандартного метода, позволяющего использовать БПФ для приближенного вычисления текущего спектра, характерно то, что интервал вычисления БПФ не скользит, а скачет. Несколько вариантов скачущего БПФ приведено на рис. 3.4, а, где представлены три из возможных способов размещения интервалов вычисления БПФ: с шагом, равным размеру БПФ, половине и четверти размера БПФ.

Вычислительная эффективность скачущего БПФ растет пропорционально величине "скачка", однако важно представить, как такой подход влияет на характер спектральных измерений. Отметим прежде всего, что скачущие измерения являются всего лишь отсчетами скользящих измерений. Следовательно, эквивалентный результат можно было бы получить, отбрасывая часть отсчетов на выходах гребенки фильтров.

Эффекты такого прореживания можно проанализировать, используя стандартную трактовку наложения частот, вспомнив, что наложение во временой области соответствует дискретизации в частотной. На рис. 3.4, б приближенно представлены эффекты наложения частотных характеристик эквивалентных фильтров для трех случаев скачущего БПФ, приведенных на рис. 3.4, а. При отсутствии перекрытия интервалов вычисления БПФ наблюдается значительное наложение частотных характеристик, что может привести к серьезным искажениям спектральных измерений. При перекрытии 2:1 и особенно 4:1 эффект наложения значительно ослабляется, хотя и остается довольно заметным. Таким образом, при увеличении перекрытия интервалов анализа частотные характеристики эквивалентных фильтров анализатора оказываются более разнесенными по частоте. На практике для

Рис. 34

борьбы с наложениями используется метод взвешивания, который позволяет уменьшить уровень боковых лепестков и тем самым ослабить эффекты наложения. В качестве приближенной оценки этого эффекта можно использовать уровень наложенного спектра (он изображен пунктирной линией) в пределах главного лепестка фильтра.

Дата добавления: 2015-05-09