Список основных символов и сокращений

Список аббревиатур

Условные обозначения, принятые в книге

▀ Скалярные переменные и скалярные функции обозначаются строчными латинскими и греческими буквами. Для обозначения преобразований от скалярных функций используются соответствующие прописные буквы.

▀ Векторы обозначаются строчными полужирными латинскими и греческими буквами.

▀ Матрицы обозначаются прописными полужирными латинскими и греческими буквами.

▀ Специальные обозначения:

Т – транспозиция вектора или матрицы;

Н – комплексно-сопряженная транспозиция вектора или матрицы;

* – комплексная сопряженность скаляра, вектора или матрицы;

^ – "крышка", используется для обозначения оценки.

АКП – автокорреляционная последовательность;

АКФ – функция автокорреляции;

АПФК – критерий авторегрессионной передаточной функции;

АР – авторегрессионная модель (параметры);

АРСС – модель (параметры) авторегрессии – скользящего среднего;

БПФ – быстрое преобразование Фурье;

ВКП – взаимнокорреляционная последовательность;

ДВПФ – дискретно-временное преобразование Фурье;

ДПФ – дискретное преобразование Фурье;

ИКА – информационный критерий Акаике;

КИХ – конечная импульсная характеристика;

ЛП – линейное предсказание;

ЛЧМ – линейная частотная модуляция;

МНСК – метод наименьших средних квадратов;

ОБПФ – обратное быстрое преобразование Фурье;

ОДПФ – обратное дискретное преобразование Фурье;

ООП – окончательная ошибка предсказания;

ОПФ – обратное преобразование Фурье;

ПФ – преобразование Фурье;

РНК – рекурсивный алгоритм наименьших квадратов;

СПМ – спектральная плотность мощности;

СС – модель (параметры) скользящего среднего;

ФВК – функция взаимной корреляции;

ЦСА – цифровой спектральный анализ.

Ap – параметр авторегрессии p-го порядка;

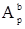– коэффициент ЛП назад р-го порядка;

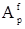– коэффициент ЛП вперед р-го порядка;

b – число разрядов цифрового числа;

Be – эквивалентная ширина полосы в герцах;

Bs – эффективная статистическая ширина полосы в Гц;

bq – параметр скользящего среднего q-го порядка;

C(k) – спектральные коэффициенты;

D{x} – дисперсия случайной переменной х;

DN(f) – дискретная функция sinc, или ядро Дирихле;

Е – энергия сигнала;

e{x(n)} – математическое ожидание случайного процесса x(n);

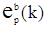– ошибка ЛП назад р-го порядка;

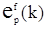– ошибка ЛП вперед р-го порядка;

f – частота в Гц;

F – интервал дискретизации по частоте в Гц;

h(n) – импульсная характеристика фильтра;

H(z) – системная функция фильтра;

Im{x} – мнимая часть комплексной переменной х;

J – матрица отражения;

k – дискретная частота;

kp=ap(p) – коэффициент отражения порядка р;

L – размер ДПФ (число спектральных отсчетов);

n – дискретное время;

N – число отсчетов данных;

{h(k,n)} – система дискретных базисных функций;

{h(k,t)} – система непрерывных базисных функций;

p – порядок АР-модели или число периодограмм;

PB(f) – оценка СПМ периодограммой Бартлетта;

PD(f) – оценка СПМ периодограммой Даньелла;

PW(f) – оценка СПМ периодограммой Уэлча;

Pxx(f) – спектральная плотность мощности;

Pxy(f) – взаимная спектральная плотность мощности;

Pxx(m) – дискретная СПМ;

q – порядок модели скользящего среднего;

Q – статистический критерий качества оценки;

rect(n) – прямоугольный импульс единичной высоты;

rxx(m) – значение АКП при временном сдвиге m;

rxy(m) – значение ВКП при временном сдвиге m;

Re{x} – вещественная часть комплексной переменной х;

SNR – линейное отношение сигнал/шум;

t – непрерывная временная переменная, секунды;

Т – интервал дискретизации по времени в секундах;

Те – эквивалентная временная протяженность в секундах;

w(n) – окно данных;

W(f) – преобразование Фурье окна данных;

Wk=Wp – коэффициенты БПФ (поворотные множители);

x(n) – функция дискретного времени;

x(t) – функция непрерывного времени;

u(n) – возбуждающий случайный процесс;

U – энергия дискретно-временного окна данных;

var{ 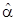} – дисперсия оценки параметра a;

z – комплексная переменная;

d(t) – дельта-функция Дирака;

d(n) – единичная импульсная функция;

Ф(m) – автокорреляционная последовательность временного окна;

sb – среднеквадратичная ошибка (дисперсия) ЛП назад;

sf – дисперсия ЛП вперед;

sfb – дисперсия ЛП вперед и назад;

– дисперсия белого шума;

w(m) – корреляционное окно;

we(m) – эффективное корреляционное окно;

W(f) – ДВПФ корреляционного окна;

We(f) – ДВПФ эффективного корреляционного окна;

Литература

1. Марпл-мл. С. Л. Цифровой спектральный анализ и его приложения: Пер. с англ. - М.: Мир, 1990.

2. Рабинер Л., Гоулд Б. Теория и применение цифровой обработки сигналов: Пер. с англ. - М.: Мир, 1978.

3. Гольденберг Л. М., Матюшкин Б. Д., Поляк М.Н. Цифровая обработка сигналов: Учеб. пособие для вузов. - М.: Радио и связь, 1990.

4. Трахтман А. М. Введение в обобщенную спектральную теорию сигналов. М.: Сов. радио, 1972.

5. Брюханов Ю. А., Кренев А. Н. Теория дискретных и цифровых сигналов и цепей: Учеб. пособие. Яросл. гос. ун-т. Ярославль, 1991.

6. Гоноровский И. С. Радиотехнические цепи и сигналы: Учебник для вузов. - М.: Радио и и связь, 1986.

7. Трахтман А. М., Трахтман В. А. Основы теории дискретных сигналов на конечных интервалах. - М.: Сов. радио, 1975.

8. Кренев А. Н. Описание сигналов с помощью разрывных функций: методические указания. Яросл. гос. ун-т. Ярославль, 1989.

Дата добавления: 2015-05-09