Моделировании исследуемого сигнала 2 страница

3) протяженность последовательности данных во времени такова, что синусоидальные компоненты имеют нечетное число четвертей периодов;

4) процентное соотношение между числом оцениваемых АР-параметров и числом используемых для этой цели отсчетов данных относительно велико.

Рис. 7.6. а - оценка методом Берга; б - оценка модифицированным ковариационным методом.

Расщепление спектральных линий отмечалось при использовании как действительных, так и комплексных данных. Спектры с расщеплением линий, как правило, содержат много ложных спектральных пиков. С ростом длины записи данных вероятность расщепления спектральных линий быстро уменьшается. Устранить расщепление линий в случае метода Юла-Уолкера можно, используя смещенную оценку АКП; в случае метода Берга - используя взвешенные квадраты ошибок. Р. Херринг полагает, что данное явление обусловлено смещением между положительными и отрицательными компонентами действительных синусоид. Не дает расщепления модифицированный ковариационный метод.

В случае процесса, состоящего из смеси одной или двух синусоид и аддитивного шума, спектральные пики авторегрессионной спектральной оценки по методу Берга оказываются сдвинутыми, причем величина их сдвига зависит от начальной фазы этих синусоид примерно по синусоидальному закону (рис. 7.7). Суинглер показал, что смещение спектральных пиков может достигать 16% величины ячейки частотного разрешения (она равна 1/NT Гц); ослабляет фазовую зависимость частотных оценок по методу Берга использование взвешенных квадратов ошибок и комплексного сигнала.

Рис. 7.7. Зависимости среднего по ансамблю положения спектральных пиков от начальной фазы косинусоидального сигнала в белом шуме.

Проведенные Наттолом исследования показали, что в случае несинусоидальных процессов лишь метод Берга и модифицированный ковариационный метод дают оценки СПМ и частоты с минимальной дисперсией. Из рис. 7.8 видно, что спектральные оценки, получаемые с помощью методов, основанных на ЛП, в целом характеризуются меньшей вариабельностью склонов, но большей амплитудой выбросов вблизи частот, соответствующих истинным пикам спектра. Они дают оценки с несколько меньшей дисперсией частоты, но с большей дисперсией СПМ, чем методы, основанные на оценивании коэффициента отражения. Большая дисперсия СПМ объясняется тем, что в случае методов, основанных на оценивании коэффициента отражения, фильтр должен быть устойчивым, а в случае методов ЛП это необязательно. Наихудшую оценку спектра АР-процесса дает метод Юла-Уолкера.

Если сигналы имеют большие уровни постоянных составляющих или же храктеризуются заметным линейным трендом, то их АР СПМ будут искажены, особенно в НЧ области спектра. Поэтому такие составляющие должны оцениваться и удаляться до выполнения процедуры АР-спектрального оценивания.

Х. Сакаи и Р. Килер показали, что дисперсия частоты АР спектральной оценки оказывается обратно пропорциональной длине записи и либо квадрату отношения сигнал/шум (для аддитивной смеси синусоид и шума), либо отношению сигнал/шум (для несинусоидальных процессов).

Г. Акаике, Р. Кроумер и К. Берк показали, что среднее значение АР-оценки СПМ оказывается в пределе равным истинному среднему значению этой оценки, а ее дисперсия стремится к значению, пропорциональному величине (4p/N)P2AP(f).

7.7. Авторегрессионное спектральное оценивание: алгоритмы

обработки последовательных данных

Алгоритмы последовательной обработки данных по мере их поступления можно рассматривать как алгоритмы с фиксированным порядком, рекурсивные относительно времени в том смысле, что они применяются для последовательной обработки данных с целью обновления оценок параметров АР-модели фиксированного порядка. Такие алгоритмы целесообразно применять в тех случаях, когда необходимо осуществлять слежение за спектром, медленно изменяющимся во времени, т. е. адаптироваться к нему, поэтому их иногда называют адаптивными алгоритмами.

Последовательные алгоритмы делятся на две категории.

1) Простейшие алгоритмы на основе градиентной аппроксимации, в том числе и метод наименьших средних квадратов (МНСК), в котором градиентная адаптивная процедура наискорейшего спуска позволяет рекурсивно оценивать p-компонентный вектор АР-параметров apT=(ap(1),..., ap(p)) в момент времени, соответствующий индексу N+1, по предыдущей его оценке, соответствующей временному индексу N. Входными параметрами являются порядок модели p и постоянная времени адаптации m. Скорость сходимости в среднем адаптивной процедуры обратно пропорциональна вличине m. Компромисс между скоростью сходимости алгоритма и точностью оценок АР-параметров достигается выбором m.

Адаптивный НСК-алгоритм был предложен Л. Гриффитсом. Он может использоваться для слежения за изменениями во времени статистик входного сигнала, если они изменяются достаточно медленно по сравнению со скоростью сходимости алгоритма. Алгоритм более функционально устойчив и менее чувствителен к квантованию, чем РНК-алгоритм. Вычислительные затраты пропорциональны p.

2) Рекурсивные алгоритмы наименьших квадратов (РНК).

Обеспечивают более высокие характеристики, чем алгоритмы НСК, но за счет дополнительных вычислительных затрат.

РНК-алгоритм позволяет по мере поступления каждого нового отсчета данных получать точное рекурсивное решение наименьших квадратов для коэффициентов ЛП. Он отличается от НСК-алгоритма тем, что адаптивный коэффициент усиления является уже не постоянной скалярной величиной, а изменяющейся во времени матрицей.

Для того, чтобы начать рекурсию, необходимо задать начальные значения вектора АР-параметров a0 и матрицы коэффициентов усиления P 0. Квадраты ошибок взвешиваются экспоненциально с коэффициентом затухания w.

Оказалось, что при продолжительной работе РНК-алгоритма в адаптивном режиме его характеристики расходятся. Это обусловлено накоплением ошибок квантования. Вычислительные затраты пропорциональны p2. Для нормальной работы РНК-алгоритма для представления чисел необходимо использовать не менее 10 двоичных разрядов, тогда как для НСК-алгоритма достаточно 7 двоичных разрядов.

Последовательные алгоритмы позволяют сразу обновлять АР параметры, а не коэффициенты отражения, что исключает необходимость применения алгоритма Левинсона и уменьшает вычислительные затраты.

Блок-схема алгоритмов последовательного во времени АР-оценивания СПМ приведена на рис. 7.9.

Рис.7.9

7.8. Некоторые практические вопросы спектрального оценивания,

основанного на линейном моделировании

7.8.1. Выбор порядка модели

Поскольку наилучшее значение порядка фильтра заранее, как правило, не известно, на практике обычно приходится испытывать несколько порядков модели. Если порядок модели выбран слишком малым, получаются сильно сглаженные спектральные оценки, если излишне большим - увеличивается разрешение, но в оценке появляются ложные спектральные пики. Дисперсия ошибки предсказания уменьшается с увеличением порядка модели монотонно и поэтому не может служить достаточным критерием окончания процедуры изменения порядка модели, пока неизвестно некоторое значение этого порядка, при дальнейшем изменении которого скорость изменения дисперсии ошибки резко снижается.

Для выбора порядка АР-модели предложено много различных критериев. Два критерия были предложены Акаике.

1) Окончательная ошибка предсказания (ООП). Согласно этому критерию, выбор порядка модели осуществляется таким образом, чтобы минимизировать среднюю дисперсию ошибки на каждом шаге предсказания. Акаике рассматривает ошибку предсказания как сумму мощностей в непредсказуемой части анализируемого процесса и как некоторую величину, характеризующую неточность оценивания АР-параметров. ООП для АР-процесса определяется выражением

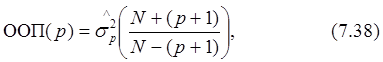
где N - число отсчетов данных, p - порядок АР-процесса и s2p- оценочное значение дисперсии белого шума, которая будет использоваться в качестве ошибки ЛП. Предполагается, что из данных вычтено выборочное среднее значение. Член в круглых скобках растет с увеличением порядка, характеризуя тем самым увеличение неопределенности оценки s2pдля дисперсии ошибки предсказания. Выбирается такое значение порядка, при котором велчина ООП минимальна. Для идеальных АР-процессов критерий ООП обеспечивает идеальные результаты.

2) Информационный критерий Акаике (ИКА) основан на методике максимального правдоподобия. Согласно этому критерию, порядок модели определяется посредством минимизации некоторой теоретико-информационной функции. Если предположить, что исследуемый АР-процесс имеет гауссовы статистики, то ИКА будет определяться следующим выражением

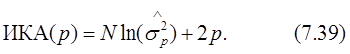
Член 2p характеризует плату за использование дополнительных АР-коэффициентов, но это не приводит к значительному уменьшению дисперсии ошибки предсказания. Выбирается порядок модели, который минимизирует значение ИКА. При N®¥ первый и второй критерии Акаике асимптотически эквивалентны.

М. Кавех и С. Бруццоне предложили вариант ИКА, который учитывает начальные условия при формулировке оценки максимального правдоподобия для АР-параметров. Отметим, что Р. Кашьяп считает ИКА статистически несостоятельным критерием в том смысле, что вероятность ошибки при выборе правильного порядка модели не стремится к нулю при N®¥, а это приводит к завышению порядка модели в том случае, когда длина записи данных возрастает. Для устранения этого недостатка Дж. Риссанен разработал другой вариант ИКА, который имеет следующую форму

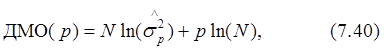
где ДМО - длина минимального описания, о которой можно сказать, что она статистически состоятельна, поскольку величина pln(N) растет с увеличением N быстрее, чем в случае с p.

3) Критерий авторегрессионной передаточной функции (АПФК) предложен Э. Парзеном. Порядок модели выбирается в этом случае равным порядку, при котором оценка разности среднего квадрата ошибок между истинным фильтром предсказания ошибки (его длина может быть бесконечной) и оцениваемым фильтром минимальна. Парзен показал, что эту разность можно вычислить, даже если истинный фильтр предсказания ошибки точно не известен

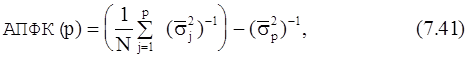
где s2j=[N/(N-j)]s2j. Значение p выбирается так, чтобы минимизировать АПФК(p).

Результаты оценивания спектра при использовании критериев ООП, ИКА и АПФК мало отличаются друг от друга, особенно в случае реальных данных, а не моделируемых АР-процессов. Т. Ульрих и Р. Клейтон показали, что в случае коротких записей данных ни один из этих критериев не обеспечивает удовлетворительных результатов. Для гармонических процессов в присутствии шума использование ООП и ИКА приводит к заниженной оценке порядка модели, особенно в тех случаях, когда отношение сигнал/шум велико. Ульрих и М. Уи экспериментально установили, что если при анализе коротких отрезков гармонических процессов с помощью ковариационного и модифицированного ковариационного методов порядок модели выбирать на интервале значений от N/3 до N/2, то во многих случаях будут получаться удовлетворительные результаты. С. Ланг и Дж. Макклеллан показали, что при использовании модифицированного ковариационного метода дисперсия положений спектральных пиков для случаев одной синусоиды или нескольких с хорошо различающимися частотами приближается к нижней границе, если порядок модели составляет примерно 1/3 длины записи данных. Тем не менее окончательный выбор порядка модели для данных, получаемых из реальных записей неизвестных процессов, пока еще носит субъективный, а не точный научный характер. Поэтому все описанные критерии целесообразно использовать лишь для выбора начального значения порядка модели, поскольку они обеспечивают хорошие результаты в случае искусственных АР-сигналов, синтезированных с помощью ЭВМ, а в случае действительных данных результаты их применения зависят от того, насколько точно эти данные могут моделироваться с помощью того или иного АР-процесса.

7.8.2. Авторегрессионные процессы с шумом наблюдения

На практике отсчеты данных очень часто искажены шумом наблюдения, что приводит к ухудшению характеристик и разрешения спектральных оценок. Это ухудшение обусловлено тем, что используемая при спектральном анализе модель с одними лишь полюсами (чисто полюсная модель) при наличии шума наблюдения оказывается уже непригодной. Пусть y(k)=x(k)+n(k) - искаженный шумом АР-процесс, где x(k) - АР(р)-процесс, а n(k) - шум наблюдения. Если n(k) - белый шум с дисперсией s2nи если он не коррелирован с x(k), то

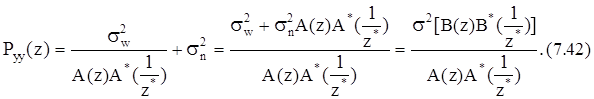
Отсюда следует, что z-преобразование АКФ выходного процесса характеризуется как полюсами, так и нулями, а это означает, что y(k) является АРСС(p,q)-процессом. Поэтому процессы этого типа следует анализировать с помощью методов на основе АРСС-моделей. Применительно к случаю, когда шум наблюдения является белым шумом, предложен ряд схем компенсации мощности этого шума, которые позволяют уменьшить связанное с ним смещение спектральных оценок. Поскольку мощность шума наблюдения влияет лишь на член АКП, соответствующий нулевому временному сдвигу,

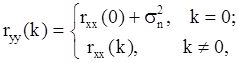
то, удаляя из оценки автокорреляционного члена ryy(0) оценку дисперсии s2n, можно устранить эффекты, обусловленные шумом наблюдения. Можно использовать метод гармонического разложения Писаренко. Аналогичные схемы компенсации можно разработать и для коэффициентов отражения. Следует, однако, отметить, что схемы компенсации шума, уменьшая смещение спектральных оценок, одновременно увеличивают дисперсию этих оценок. Основной их недостаток состоит в том, что заранее неизвестно, какую долю мощности шума следует удалить; если оценка s2nслишком велика, то оцененный АР-спектр будет иметь более острые спектральне пики, чем истинный спектр.

7.8.3. Оценивание мощности синусоидальных компонент

АР-метод оценивания СПМ часто используется для того, чтобы выявить в данных наличие синусоидальных компонент. Мощности, соответствующие компонентам в оценке СПМ, можно точно вычислить, интегрируя площадь под кривой этой оценки. Однако это связано с большими вычислительными затратами. Для классических спектральных оценок надежным показателем относительной мощности служит высота пиков, т. к. в случае, когда анализируемый процесс состоит из аддитивной смеси синусоид и белого шума, высота спектральных пиков прямо пропорциональна мощности этих синусоид. Но для АР-оценок СПМ такой метод не применим. Р. Лакосс показал, что авторегрессионная m-го порядка СПМ для процесса, состоящего из одной синусоиды и белого шума, достигает своего максимума при f=f0

где SNR=P/s2 и предполагается mSNR>>1 (т. е. что отношение сигнал/шум велико). Таким образом, высота пика оказывается пропорциональной квадрату мощности, а следовательно, площадь под пиком прямо пропорциональна этой мощности.

Метод оценки мощности нескольких действительных синусоид по пикам в АР-спектре был предложен С. Джонсоном и Н. Андерсеном. Однако он дает хорошие результаты только в случае достаточно разнесенных спектральных пиков синусоид с высоким отношением сигнал/шум. Если АР-СПМ записать в виде z-преобразования

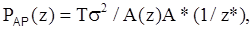
то мощность пика, наблюдаемого в АР-спектре на частоте fk, будет оцениваться следующей величиной:

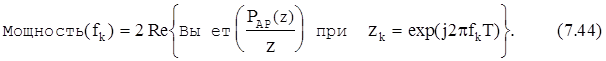
7.8.4. Частотное разрешение

Следует заметить, что степень улучшения разрешения оценки АР СПМ в случае процессов, состоящих из смеси синусоид и белого шума, зависит от величины отношения сигнал/шум. Степень разрешения синусоид равной мощости в случае известной автокорреляционной последовательности можно определить с помощью приближенной формулы С. Л. Марпла-мл.:

где F - разрешение в Гц,

Т - интервал отсчетов в секундах,

р - максимальное значение индекса временного сдвига для АКП,

SNR - линейное отношение сигнал/шум для отдельной синусоиды.

7.9. Метод Прони

Метод Прони - метод моделирования выборочных данных в виде линейной комбинации экспоненциальных функций. С помощью метода Прони осуществляется аппроксимация данных с использованием некоторой детерминированной экспоненциальной модели, в противоположность АР-методам, с помощью которых стремятся приспособить вероятностные модели представления статистик 2-го порядка для имеющихся данных.

В оригинальной статье Г. Прони описан метод точной подгонки, основанный на использовании такого большого числа полностью затухающих экспонент, сколько их необходимо для аппроксимации N имеющихся точек данных. Современный вариант метода Прони обобщен и на модели, состоящие из затухающих синусоид. В нем также используется анализ по методу наименьших квадратов для приближенной подгонки экспоненциальной модели в тех случаях, когда число точек данных превышает их число, необходимое для подгонки с помощью предполагаемого числа экспоненциальных членов. Одна из модификаций современного метода Прони позволяет использовать чисто синусоидальную модель с незатухающими компонентами.

Предположим, что имеется N комплексных отсчетов данных {x(1),..., x(N)}. Тогда метод Прони позволяет оценить x(n) с помощью некоторой p-членной модели комплексных экспонент

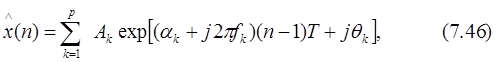
где 1£n£N, T - интервал отсчетов в секундах, Akи ak- амплитуда и коэффициент затухания (в с-1) k-й комплексной экспоненты, fkи qk- частота (в Гц) и начальная фаза (в рад) k-й синусоиды. Значения всех этих параметров полностью произвольны. В случае отсчетов действительных данных комплексные экспоненты должны появляться комплексно-сопряженными парами равной амплитуды, что сводит экспоненциальное представление к

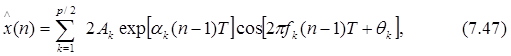
где 1£n£N. Если число p комплексных экспонент четно, то будем иметь p/2 затухающих косинусоид. Если p нечетно, то будем иметь (p-1)/2 затухающих косинусоид и одну полностью затухающую экспоненту.

7.9.1 Исходный метод Прони

Если число используемых отсчетов данных равно числу экспоненциальных параметров, то возможна точная подгонка экспонент под имеющиеся данные. Рассмотрим функцию дискретного времени, представляющую собой сумму p экспонент:

где комплексные константы hkи zkопределяются выражениями

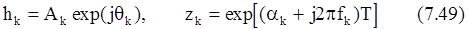или в матричной форме

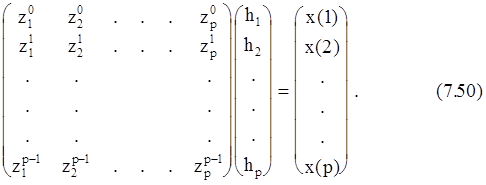
Эти уравнения можно разделить по параметрам hkи zk, т. к. уравнение (7.50) является решением некоторого однородного линейного разностного уравнения с постоянными коэффициентами. Определим сначала полином ф(z) с комплексными коэффициентами a(m), a(0)=1, корнями которого являются экспоненты zk

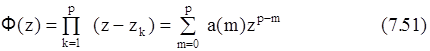
Осуществляя сдвиг индекса от n к n-m и умножая обе его части на параметр a(m), получаем

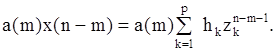
Записывая аналогичные произведения a(0)x(n),..., a(m-1)x(n-m+1) и осуществляя суммирование, получим

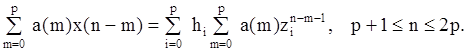
Осуществляя подстановку zin-m-1=zin-pzip-m-1, получим

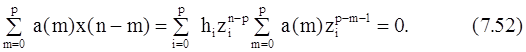
Сумму в правой части (7.52) можно рассматривать как полином, определяемый уравнением (7.51), который записан через свои корни, что и обеспечивает в (7.52) равенство нулю. Уравнение (7.52) - это линейное разностное уравнение, однородное решение которого выражается формулой (7.48). Полином (7.51), ассоциированный с этим линейным разностным уравнением, называется характеристическим.

p уравнений, представляющих истинные значения коэффициентов a(m), удовлетворяющих уравнению (7.52), можно записать в виде следующего (pхp)-матричного уравнения

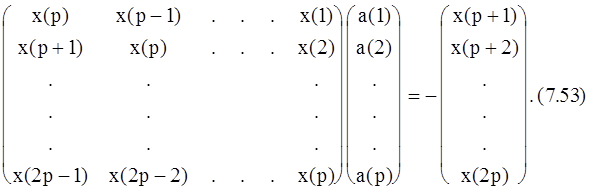
Процедуру Прони для подгонки p экспонент к 2p отсчетам можно теперь представить в виде следующих трех этапов. На первом этапе получается решение уравнения (7.53) для коэффициентов полинома. На втором этапе вычисляются корни полинома, определяемого уравнением (7.51). Используя корень zi, можно определить коэффициент затухания aiи частоту синусоиды fiс помощью соотношений

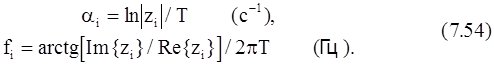
На третьем этапе корни полинома, вычисленные на втором этапе, используются для формирования элемементов матрицы уравнения (7.50), которое затем решается относительно p комплексных параметров h1,..., hp. Амплитуда Aiи начальная фаза qi

находятся как:

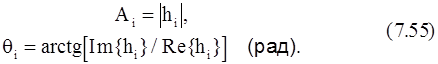
Краткая запись метода экспоненциального оценивания Прони и вычисления СПЭ по методу Прони приведена на рис. 7.10.

Рис. 7.10

7.9.2. Метод наименьших квадратов Прони

На практике число отсчетов данных N обычно превышает то минимальное их количество, которое необходимо для подгонки модели из p экспонент, т. е. N>2p. В этом переопределенном случае последовательность отсчетов данных может быть аппроксимирована лишь приблизительно с ошибкой аппроксимации e(n)=x(n)-x(n).

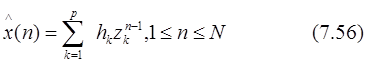
Одновременное отыскание порядка p и параметров {hk,zk}, 1£k£p, минимизирующих сумму квадратов ошибки

представляет собой трудную нелинейную задачу. Используя на первом и втором этапах метода Прони линейные процедуры НК, получим обобщенный метод Прони. В переопределенном случае линейное разностное уравнение (7.52) имеет вид:

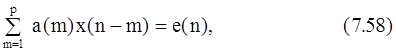
где p+1£n£N. Член e(n) характеризует ошибку аппроксимации на основе ЛП в отличие от ошибки экспоненциальной аппроксимации e(n). Уравнение (7.58) идентично уравнению для ошибки ЛП вперед, и тепрь парамеры a(m) из уравнения (7.52) можно выбирать как параметры, которые минимизируют не сумму (7.57), а сумму квадратов ошибок ЛП

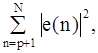
Получим ковариационный метод ЛП. Существенно ограничение порядка: p£N/2.

Метод Прони не позволяет получить оценку шума отдельную от сигнала. Модель Прони, учитывающая присутствие аддитивного шума, будет иметь форму

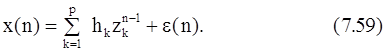
Если в исходной процедуре Прони вместо x(n) использовать x(n)-e(n), то линейное разностное уравнение, которое описывает процесс, состоящий из суммы экспонент и аддитивного белого шума, будет иметь вид

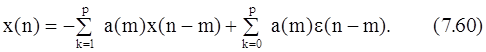
На первом этапе метода Прони используется уравнение линейного предсказания

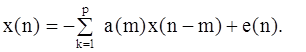
и попытка "отбеливания" e(n). Сравнивая два последних уравнения, видим, что отбеленный процесс e(n) совершенно не соответствует небелому СС-процессу, представленному выражением

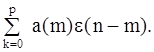
Рис. 7.11. а - обобщенный метод Прони, р=15; б - модифицированный метод Прони, p=16.

Метод Прони не позволяет учесть наличие небелого шума в анализируемом процессе, поэтому при наличии сильного аддитивного шума получаются очень неточные, завышенные оценки коэффициентов затухания. Использование значений p, превышающих число действительно имеющихся полюсов, упрощает моделирование и позволяет учесть наличие шума.

Обычный МНК Прони может быть модифицирован для аппроксимации последовательности комплексных данных с помощью модели, состоящей из незатухающих комплексных синусоид - модифицированный метод Прони.

На рис. 7.11 показаны оценки по методу Прони СПЭ, полученные для 64-точечной тест-последовательности данных. Модифицированный метод Прони дает линейчатый спектр, т. к. в нем используется допущение о синусоидальной модели. Получаются очень точные оценки четырех действительных синусоид сигнала, но неточное представление окрашенного шума.

Дата добавления: 2015-05-09