Моменты второго порядка (среднее значение квадрата и дисперсия)

Эргодические случайные процессы

В предыдущем разделе был рассмотрен вопрос об определении свойств случайного процесса путем осреднения по ансамблю в отдельные моменты времени. Однако в большинстве случаев, возможно, также описать свойства стационарного случайного процесса путем осреднения по времени отдельных выборочных функций ансамбля. Рассмотрим, например, k-ю выборочную функцию случайного процесса, изображенного на рис. 7. Среднее значение m_x(k) и автокорреляционная функция R_x(t, k)этой выборочной функции определяются выражениями:

Если случайный процесс {x(t)} стационарен и определенные данными формулами m_x(k) и R_x(t, k)одинаковы для различных выбороч­ных функций, то случайный процесс {x(t)} называется эргодическим. Для эргодического случайного процесса среднее значение и автокорреляционная функция (а также и другие моменты, полученные осреднением по времени) равны соответствующим средним по ансамблю: m_x(k) = m_x и R_x(t, k) =R_x(t). Следует заметить, что только стационарные процессы могут обладать свойством эргодичности.

Элементарное представление о суммарной интенсивности лю­бого случайного процесса дает среднее значение квадрата, которое представляет собой просто среднее из всех значений квадрата процесса в пределах данной реализации. Среднее значение квад­рата Y² данной реализации x(t) определяется в виде:

Абсолютная величина корня квадратного из среднего значения квадрата называется среднеквадратичным значением.

Зачастую удобно рассматривать физический процесс в виде суммы статической, т. е. не зависящей от времени, составляющей и динамической, или флуктуационной, составляющей. Статиче­скую составляющую можно получить, вычисляя среднее значение, которое представляет собой просто среднее из всех значений процесса. Среднее значение равно:

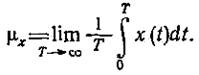
Динамическая составляющая определяется дисперсией процесса - величиной, равной просто среднему квадрату отклонений его ординат от среднего значения. Дисперсия процесса равна:

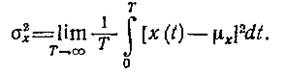
Положительное значение корня квадратного из дисперсии называется среднеквадратичным отклонением.

Раскрывая скобки в подынтегральной функции данной формулы находим, что дисперсия равна разности между средним значением квадрата и квадратом среднего значения

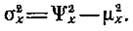
Дата добавления: 2015-05-09