Автокорреляционная функция

Автокорреляционная функция случайного процесса характеризует общую зависимость значений процесса в некоторый данный момент времени от значений в другой момент. Рассмотрим реализацию x(t), приведенную на рис. 8.

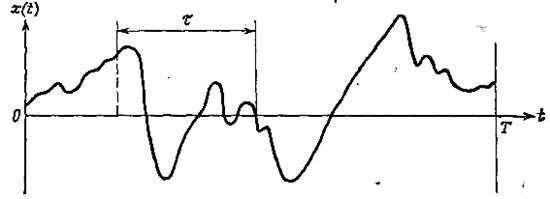
Рис. 8. Определение автокорреляционной функции

Оценку величины автокорреляционной функции, связывающей значения x(t) в моменты времени t и t₁ + t,можно получить, вычисляя произведение этих ординат и осредняя величину произведения в пределах времени наблюдения Т. Найденное среднее значение произведения приближается к точному значению автокорреляционной функции при стремлении Т к бесконечности:

Величина R_x(t) — всегда действительная четная функция с мак­симумом в точке t =0; она может быть как положительной, так и отрицательной. Запишем эти утверждения в виде формул:

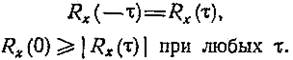
Среднее значение функции x(t) выражается через автокорреляционную функцию (исключая некоторые особые случаи, как, например, гармоническое колебание) выражается:

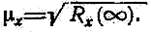
Таким образом, среднее значение функции x(t) равно положительному значению корня квадратного из автокорреляционной функции, взятой при очень большом сдвиге. Аналогично среднее значение квадрата функции равно:

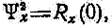
т. е. среднее значение квадрата равно значению автокорреляцион­ной функции при нулевом сдвиге.

Примеры. На рис. 9 показаны типичные графики автокорреляционных функций (зависимости R от сдвига t). Эти гра­фики называются автокоррелограммами. Имеющая вид косинусоиды автокоррелограмма гармонического колебания (рис. 9,а) описывается соотношением:

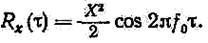
Важная особенность этой автокоррелограммы заключается в том, что форма ее периодически повторяется во времени с тем же периодом, что и период рассматриваемого гармонического колебания, но информация о фазе теряется.

Автокоррелограмма, имеющая вид крутого пика с быстрым спаданием к нулю (рис. 9, г), типична для широкополосного случайного процесса с нулевым средним значением (если среднее значение не равно нулю, автокорреляционная функция стремится к величине m_x²). В предельном гипотетическом случае белого шума (случайный процесс, энергия которого равномерно распределена по всем частотам) автокоррелограмма имеет вид дельта-функции Дирака при нулевом значении сдвига (t =0).

Автокоррелограмма суммы гармонического колебания и случайного шума представляет собой просто сумму автокоррелограмм гармонического колебания и случайного шума (рис. 9, б). С другой стороны, автокоррелограмма узкополосного случайного шума (рис. 9, в)напоминает автокоррелограмму гармонического колебания с затухающей амплитудой. Важной ее особенностью является то, что она стремится к нулю при больших значениях сдвига (если m_x =0). Четыре графика на рис. 9 показывают, как меняется вид автокоррелограмм при переходе от гармонического процесса к широкополосному случайному процессу.

Рис. 9. Графики автокорреляционных функций (автокоррелограммы)

а - гармонический процесс; б - сумма гармонического процесса и случайного шума; в - узкополосный случайный шум; г - широкополосный случайный шум.

Дата добавления: 2015-05-09