Оценка входных величин и их стандартных отклонений (неопределенностей)

Пусть имеются результаты n_i измерений входной величины X_i, где i = 1…m. Как известно, при нормальном распределении наилучшей оценкой этой величины является среднее арифметическое

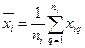(2)

Стандартную неопределенность типа А определяют как среднеквадратическое отклонение по формуле:

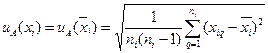(3)

Для вычисления стандартной неопределенности по типу В используют:

- данные о предыдущих измерений величин, входящих в уравнение измерения;

- сведения, имеющиеся в метрологических документах по поверки, калибровки и сведения изготовителя о приборе;

- сведения о предполагаемом вероятностном распределении значений величин, имеющихся в научно-технических отчетах и литературных источниках;

- данные, основанные на опыте исследователя или общих знаниях о поведении и свойствах соответствующих (подобных) СИ и материалов;

- неопределенность используемых констант и справочных данных;

- нормы точности измерений, указанные в технической документации на методы и СИ;

- другие сведения об источниках неопределенностей, влияющих на результат измерения.

Неопределенности этих данных обычно представляют в виде границ отклонения значения величины от ее оценки. Наиболее распространенный способ формализации неполного знания о значении величины заключается в постулировании равномерного закона распределения возможных значений этой величины в указанных границах (нижней b_i- и верхней b_i+) для i- ой входной величины. При этом стандартную неопределенность по типу В определяют по известной формуле для среднеквадратического отклонения результатов измерений, имеющих равномерный закон распределения:

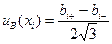, (4)

а для симметричных границ 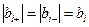, по формуле

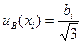(5)

В случае других законов распределений формулы для вычисления неопределенности по типу В будут другие. В частности, если известно одно значение величины X_i, то это значение принимается в качестве оценки. При этом стандартную неопределенность вычисляют по формуле

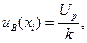(6)

где U_p – расширенная неопределенность, k – коэффициент охвата. Если коэффициент охвата не указан, то, с учетом имеющихся сведений, принимают предположение о вероятностном распределении неопределенности величины X_i. Если такие сведения отсутствуют, то для определения коэффициента охвата можно воспользоваться данными таблицы 2 [1,3].

Таблица 2

Предполагаемое распределение неопределенности входной величины	Вероятность охвата Р, которой соответствует U(xi)	Коэффициент охвата k
Равномерное распределение	0,99 – 1,0	1,71 - 1,73
0,95	1,65
Нормальное распределение	1,0 (предел допускаемых значений)
0,997
0,99	2,6
0,95
Неизвестное распределение

Примечание к таблице 2. Коэффициенты охвата для равномерного распределения определены следующим образом. Для симметричных границ окончательного равномерного распределения СКО вычисляется по формуле (5). Тогда расширенную неопределенность можно записать в виде 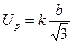. При расширенной неопределенности, соответствующей вероятности P=0,95 и границе равномерного распределения b=1, коэффициент k=0,95 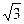= 1,65, при расширенной неопределенности, соответствующей вероятности P=0,99, коэффициент k= 0,9995 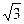= 1,71. При расчетах принималось, что 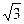=1,73 и площадь под равномерным распределением соответствует единице и, соответственно, при Р=1, k=1,73.

Если известны граница суммы неисключенных систематических погрешностей, распределенных по равномерному (равновероятному) закону θ(Р) или расширенная неопределенность в терминах концепции неопределенности U_p, то коэффициенты охвата при числе неисключенных систематических погрешностей m>4, зависит от доверительной вероятности. Коэффициент охвата k=1,1 при Р=0,95; k=1,4 при Р=0,99 [1,3].

Неопределенности входных величин могут быть коррелированны. Для вычисления коэффициента корреляции r(x_i, x_q) используют согласованные пары результатов измерений 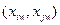, где w = 1, 2, …n_ij ; n_ij – число согласованных пар результатов измерений 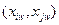Вычисления проводят по известной формуле из статистики и теории вероятности

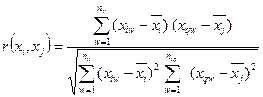(7)

Значимость коэффициента корреляции определяется критерием отсутствия или наличия связи между аргументами [3].

Дата добавления: 2015-05-26