Метод циліндричних шарів

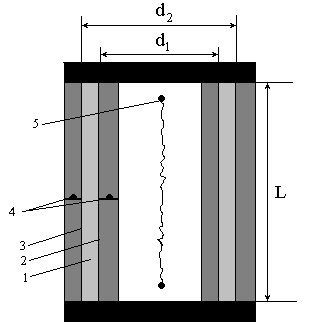
Останнім часом широко використовується метод циліндричного шару (рис. 2.5), особливо при дослідженні теплопровідності роз­плавлених металів і напівпровідників. Речовина 1 заповнює про­міжок між коаксіальними циліндрами 2 і 3, де створюється сталий градієнт температури, який вимірюють термопарами 4.

Рис. 2.5. Метод коаксіальних циліндрів: 1 – досліджувана речовина; 2,3 – коаксіальні циліндри; 4 – термопари; 5 – нагрівач.

Кількість теплоти, що проходить за одиницю часу в стаціонарному стані через бокову поверхню довільного циліндру між внутрішнім і зовнішнім циліндрами дорівнює:

.

І ця кількість теплоти постійна для довільного циліндричного шару.

Граничні умови для цієї задачі:

1) , Т = Т₂,

2) r = d₁ / 2, T = T₁.

В результаті розв’язку крайової задачі коефіцієнт теплопровідності визначають за формулою для циліндричного шару:

де — кількість теплоти, яку виділяє нагрівник 5 у внутрішньо­му циліндрі за одиницю часу; — довжина твірної циліндра; d₁, d₂ — внутрішній діаметри циліндричного шару зразка; T₁, T₂ — температури внутрішнього і зовнішнього шарів зразка.

2.5. Визначення коефіцієнта теплопровідності металевого стержня (Метод Бората-Вінера)

Розглянемо розповсюдження теплоти в прямому однорідному стержні з постійним поперечним перерізом, будь якої геометричної конфігурації (прямокутник, коло, трикутник, та інше). На одному з кінців стержня знаходиться джерело тепла з постійною температурою Т₀. Сам стержень, і його другий кінець знаходяться у середовищі з температурою Т_g, яка також не змінюється (Т_g<Т₀). Обмін теплом між нагрітим стержнем і відносно холодним середовищем відбувається через бічну поверхню стержня.

При невеликій різниці температур стержня й середовища (Т-Т_g), цей процес теплообміну з достатньою точністю може бути описаний за допомогою закону Ньютона-Ріхмана:

.

Тут - кількість теплоти, якою із середовищем за одиницю часу, α – коефіцієнт теплообміну, S_side – площа бічної поверхні стержня. Рівняння має інтегральний характер. Узагалі, температура стержню є функцією координат стержню Т(x,y,z). Якщо вважати, що коефіцієнт теплообміну не залежить від температури α=const (зазвичай коефіцієнт теплообміну α зростає із підвищенням температури). Саме вид цієї функції визначає, як відбувається обмін тепла між стержнем і середовищем в будь-якій точці на бічній поверхні стержню.

Пошук розподілу температури у стержні значно спроститься, якщо не враховувати зміну температури впоперек стержню, тобто вважати, що температура стержню змінюється тільки вздовж вісі Ox. Це припущення буде тим більш справедливим, чим менше критерій Bi<<1 для стержня (Критерій уявляє з себе відношення величин, які характеризують інтенсивність потоку тепла з поверхні стержня у навколишню середу порівняно з інтенсивністю потоку тепла до поверхні стержню з його маси.).

Виділимо довільний елемент стержню довжиною dx на відстані x від місця контакту стержня з джерелом тепла, і складемо для нього рівняння теплового балансу:

.

Тут – кількість тепла, що входить через площу поперечного перерізу S у ліву грань елементу за одиницю часу, - кількість тепла, що виходить із протилежної грані елементу за той же час, – кількість тепла, яким обмінюється за одиницю часу елемент стержню з навколишнім середовищем через бічну поверхню елементу.

Останню величину, можна знайти, використовуючи вже згаданий закон Ньютона-Ріхмана: . Тут враховано, що для елементу стержня S_side=pdx, де p - периметр поперечного перерізу стержню, і для зручності подальших розрахунків відлік температури встановлено від температури середи T_g. Отримана таким чином надлишкова температура позначена як .

Величини і можуть бути визначені за допомогою закону Фур’є:

Прирівніючи їх, одержуємо стаціонарне диференційне рівняння теплопровідності стержню: , або

причому , де T₀ – температура зовнішнього середовища; а – коефіцієнт тепловіддачі; p –периметр поперечного перерізу стержня; S – площа поперечного перерізу стержня; l – коефіцієнт теплопровід­ності. Розв'язок рівняння має вигляд

.

Припустивши, що при x = 0, T = T₁, а стержень нескінченно довгий, тобто при x = ¥, Т=Т₀ отримаємо

,

звідки

.

Кількість теплоти, що розсіюється бічною поверхнею стержня,

(2.9)

можна записати у вигляді

.

Проінтегрувавши вираз у межах від 0 до ¥, отримаємо

. (2.10)

Згадавши, що є коефіцієнт а можна знайти вираз для коефіцієнту теплопровідності:

; . (2.11)

Для визначення теплопровідності за даною формулою необхідно знати кількість тепла q,що віддається стержнем при стаціонар­ному режимі через поверхню, температуру нагрітого кінця стерж­ня T₁,температуру Ту будь-якій точці х стержня, віддаленій від нагрітого кінця, площу поперечного перерізу стержня S і темпера­туру зовнішнього середовища T₀.

Звичайно, практично неможливо мати нескінченно довгий стер­жень, однак чим він довший, тим точніше можна визначити коефі­цієнт теплопровідності. Знайдемо похибку Dq, вважаючи, що стер­жень має довжину L.Проінтегрувавши рівняння (2.19) у межах від x = Lдо x = ¥, отримаємо:

Розділивши це співвідношення на вираз (2.10), отримаємо

.

Даний вираз і дає величину похибки за рахунок скінченої дов­жини стержня L.

Визначимо теплопровідність латунного стержня, кінець якого нагрівають в електропечі (рис. 2.6.). Кількість теплоти, що від­дає нагрівальний елемент за одиницю часу, обчислюють за формулою Q=I₀U₀, температуру T₁печі — за допомогою термопари 6. Теп­лота частково витрачається на утворення теплового потоку qза рахунок теплопровідності, частково – виводиться в зовнішнє середовище q₁:

Q = q + q₁.

Якщо витягнути стержень із печі, не допускаючи зміни темпе­ратури T₁(температура печі зі стержнем), можна визначити кіль­кість теплоти, що видаляєтеся в зовнішнє середовище:

q₁ =I₁U₁,

де I₁ і U₁ – сила струму і напруги на печі без стержня. Таким чином,

q = I₀U₀ – I₁U₁.

Для зменшення похибки при визначенні qнеобхідно, щоб q₁ << q,тому піч поміщають у посудину Дьюара. Температура сте­ржня Tвимірюється термопарами 1 – 5. Температура зовнішнього середовища Т₀ототожнюється з температурою води, яка циркулює у кожусі. Оскільки не потрібно визначати абсолютні значення тем­ператур у різних точках стержня (у формулу входять лише різ­ниці їх), то один кінець кожної термопари поміщають у проточну воду.

Рис. 2.6. Експериментальна установка для реалізації методу Барата-Вінера

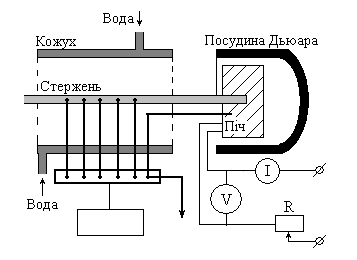
При вимірюванні визначають площу поперечного перерізу S досліджуваного стержня, для чого вимірюють масштабною ліній­кою його довжину L, а також відстань xвід кінця стержня, що зна­ходиться в печі, до кожної з п'яти термопар, мікрометром – діа­метр. Після цього кінець стержня встановлюють так, щоб він щіль­но входив в отвір печі, включають піч і відкривають водопровідний кран. Вимірювання здійснюють після встановлення теплової рів­новага, тобто коли показання всіх термопар не міняються. Потім відтягують піч і, зменшуючи силу струму, добиваються поперед­ніх показів термопари печі 6; одночасно записують покази вольт­метра й амперметра:

Q = l (I₀U₀ – I₁U₁).

По осі xвідкладають відстані від термопар до гарячого кінцястержня, по осі y – величини , що утворюють пряму, що утворюють пряму, яка описується рівнянням

.

За цими точками знаходять кутовий коефіцієнт а даної пря­мої і, підставивши його значення у формулу (2.11), одержують коефіцієнт теплопровідності стержня.

Дата добавления: 2015-05-26