Кодирование факторов

Полный факторный эксперимент

К оптимизации приступают при наличии некоторых результатов предварительных исследований изучаемого объекта. После выбора критерия оптимизации, отсеивания несуществующих факторов выбирают область эксперимента. Выбор этой области производят на основе анализа априорной информации. В области эксперимента устанавливают основные уровни и интервалы варьирования.

Для удобства записи условий эксперимента и обработки данных уровни факторов кодируют. Кодирование производят исходя из соотношения (13.5):

X_i = (X_{(i max (min))} – X_oi) / E_i, (13.5)

где X_i - кодированное значение i–го фактора; X_{i max (min)} - натуральное значение i–го фактора соответственно на верхнем и нижнем уровнях; X_oi - натуральное значение i–го фактора в нулевой точке; E_i - интервал варьирования i–го фактора.

В кодированном виде верхний уровень обозначают +1, нижний -1, а основной – 0. Материал, иллюстрирующий кодирование факторов, приведён в табл. 13.1.

Таблица 13.1

Наименование фактора	Единица измерения	Значение нулевого (основного) уровня	Интервал варьирования	Значение верхнего уровня	Значение нижнего уровня
натураль-ное	кодированное	натуральное	Кодирован-ное
натуральное	кодирован-ное
Температура	град.					+1		-1
Давление	мПа			0.5	5.5	+1	4.5	-1
Время	сек.					+1		-1

Например, пусть фактором будет температура и натуральное значение его в нулевой точке X_io = 160⁰. При интервале варьирования

Е = 10⁰ верхний уровень фактора имеет значение:

X_{i max} = X_io + E = 160 + 10 = 170⁰;

и нижний его уровень:

X_{i min} = X_io – E = 160 –10 = 150⁰.

Тогда кодированные значения фактора будут:

X_i^В = (170 – 160)/10 = +1;

X_i^Н = (150 – 160)/10 = -1.

Эксперимент, в котором реализуются все возможные сочетания факторов на выбранных уровнях, называется полным факторным экспериментом (ПФЭ).

Число опытов N в полном факторном эксперименте определяется выражением:

N = m^k, (13.6)

где m – число уровней каждого фактора; k – число факторов.

Первый этап планирования эксперимента для получения линейной модели основан на варьировании факторов на двух уровнях, следовательно:

N = 2^k.

Факторный эксперимент осуществляют с помощью матрицы планирования, которая даёт максимальную информацию о действии факторов и их взаимодействиях на параметры оптимизации. При построении матрицы ПФЭ следует учитывать следующее. Число строк равно количеству опытов N. Уровни факторов обозначаются кодированными значениями (+1; -1). Для упрощения записи условий эксперимента в матрице планирования вместо «+1» и «-1» пишут только «+» или «-». Значения функции отклика, полученные при выполнении опытов обозначаются через у₁, у₂, …, у_п.

Моделью объекта будет уравнение (13.7):

y = b₀ + b₁x₁ + b₂x₂ + … + b₁₂x₁x₂ + … + b₁₂₃x₁x₂x₃ + …. (13.7)

Значения коэффициентов в этом уравнении определяют с помощью значений функции отклика, полученных в результате опытов. Величина и знак коэффициента указывают на вклад данного фактора в общий результат при переходе с нулевого на верхний или нижний уровень фактора. Коэффициенты при факторах учитывают непосредственное воздействие фактора на параметр оптимизации, а коэффициенты при произведениях факторов учитывают тот факт, что влияние одного фактора может зависеть от уровня, на котором находятся другой или другие. Линейным называют эффект, характеризующий линейную зависимость параметра оптимизации от соответствующего фактора. Эффектом взаимодействия называют эффект, характеризующий совместное влияние нескольких факторов на параметр оптимизации.

Взаимодействие называется парным (первого порядка), если взаимодействуют два фактора (модель содержит произведения двух факторов); тройным (второго порядка), если взаимодействуют три фактора и т. д. ПФЭ даёт возможность количественно оценить линейные эффекты и все эффекты взаимодействия, получая при этом несмешанные оценки коэффициентов.

Смешанной называют оценку, когда какой-либо коэффициент (или коэффициенты) учитывают влияние не только фактора (или взаимодействия) при котором он стоит, но и влияние других факторов и (или) взаимодействий. При отсутствии этого оценка коэффициента называется несмешанной.

Рассмотрим на примере ПФЭ 2³ построение матрицы планирования. Уравнение регрессии для трёхфакторного эксперимента имеет следующий вид:

y = b₀ + b₁x₁ + b₂x₂ + b₃x₃ + b₁₂x₁x₂ + b₁₃x₁x₃ + b₂₃x₂x₃ + b₁₂₃x₁х₂ х₃. (13.8)

Матрица этого эксперимента приведена в табл. 13.2, где в первом столбце проставлены номера опытов, второй – представляет собой значения фиктивного фактора X₀ (он введён для оценки свободного члена b₀ и находится всегда на верхнем уровне), третий, четвёртый и пятый столбцы представляют собой матрицу ПФЭ 2³.

Таблица 13.2

План ПФЭ 2³ с взаимодействиями

№ опыта	Х0	Х1	Х2	Х3	Х1Х2	Х1Х3	Х2Х3	Х1Х2Х3	У
	+	-	-	-	+	+	+	-	у1
	+	+	-	-	-	-	+	+	у2
	+	-	+	-	-	+	-	+	у3
	+	+	+	-	+	-	-	-	у4
	+	-	-	+	+	-	-	+	у5
	+	+	-	+	-	+	-	-	у6
	+	-	+	+	-	-	+	-	у7
	+	+	+	+	+	+	+	+	у8

Для построения матрицы, т.е. для определения всех возможных сочетаний уровней факторов, существуют различные методики. Рассмотрим наиболее простую. Согласно этой методике элементы первой строки матрицы имеют отрицательный знак, знак элементов первого столбца (х₁) чередуется через один, второго – через два, третьего – через четыре, четвёртого – через восемь и т.д. по степеням двойки (см. табл. 13.3).

Шестой, седьмой, восьмой и девятый столбцы отведены под взаимодействия всех возможных вариантов. Знаки в этих столбцах получены путём перемножения столбцов соответствующих факторов.

Третий, четвёртый и пятый столбцы используют как для проведения эксперимента (ибо они содержат уровни факторов в опытах), так и для расчёта оценок коэффициентов модели, а второй, шестой, седьмой, восьмой и девятый только для расчёта коэффициентов модели.

Расположение экспериментальных точек в факторном пространстве для ПФЭ при к = 2 и к = 3 показано на рис. 13.6. Как видим, точки плана 2² задаются координатами вершин квадрата, а точки 2³ – вершин куба.

Таблица 13.3

Схема построения матрицы при увеличении

числа факторов от 2 до 4

	Х1	Х2	Х3	Х4
	-	-	-	-
	+	-	-	-
	-	+	-	-
	+	+	-	-
	-	-	+	-
	+	-	+	-
	-	+	+	-
	+	+	+	-
	-	-	-	+
	+	-	-	+
	-	+	-	+
	+	+	-	+
	-	-	+	+
	+	-	+	+
	-	+	+	+
	+	+	+	+

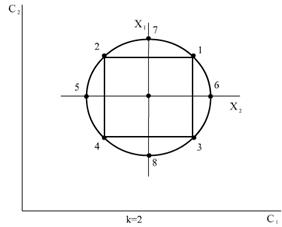
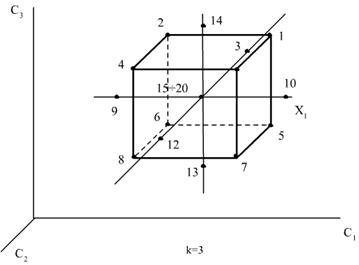
Рис. 13.6. Расположение точек в факторном пространстве

Дата добавления: 2015-05-26