Обработка результатов эксперимента

Рандомизация

Перед проведением эксперимента следует оценить условия, в которых он будет проходить. Под условиями в данном случае понимается наличие возмущающих и контролируемых входных параметров объекта, таких, как температура окружающей среды, её влажность, изменение характеристик образцов, используемых в эксперименте,

и т.п. Если условия могут изменяться непредсказуемым образом, то исключить их влияние можно с помощью приёма, называемого рандомизацией, которая заключается в реализации плана эксперимента таким путём, чтобы влиянию условий придать случайный характер.

Для исключения систематических ошибок рекомендуется опыты, предусмотренные матрицей, проводить в случайной последовательности. Порядок проведения опытов следует выбирать по таблице случайных чисел или путём обычной жеребьёвки.

Для компенсации влияния случайных погрешностей каждый опыт необходимо проводить n раз. Опыты, проводимые несколько раз при одних и тех же значениях факторов, называются параллельными. Под дублированием понимают постановку параллельных опытов. Обычное число параллельных опытов принимают равным 2-3, иногда 4-5. Существует три варианта дублирования опытов: 1 – равномерное, 2 – неравномерное, 3 – без дублирования.

При равномерном дублировании все строки матрицы планирования имеют одинаковое число параллельных опытов. В случае неравномерного дублирования числа параллельных опытов неодинаковы. При отсутствии дублирования параллельные опыты не проводятся. Наиболее предпочтительным является первый вариант, при котором эксперимент отличается повышенной точностью, а математическая обработка данных – простотой.

Использование приёма рандомизации покажем на примере. Допустим, необходимо провести ПФЭ 2², причём в каждом опыте предполагается осуществить два наблюдения. ПФЭ 2² предполагает проведение четырёх опытов, а с учётом параллельных опытов в нашем примере – 8. Теперь выберем в таблице случайных чисел (прил. 6) ряд чисел с 1 по 8, допустим следующий: 4, 2, 5, 6, 7, 3, 8 и 1 (ряд не должен иметь повторений). Следовательно, именно такую последовательность должны иметь наблюдения (табл. 13.6).Это значит, что по времени будут начинать с опыта № 4 (порядковый номер 8), затем выполнять опыт № 1 (порядковый номер 2) и т. д.

Таблица 13.6

Рандомизированная матрица планирования

№ опыта	Х0	Х1	Х2	Порядковый № опыта и его повторения	Случайная последовательность выполнения опытов
	+	-	-
	+	+	-
	+	-	+
	+	+	+

Обработку результатов эксперимента при равномерном дублировании опытов можно представить следующей схемой.

1. Для каждой строки матрицы планирования вычисляют среднее арифметическое значение у_j параметра оптимизации:

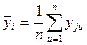, (13.14)

где 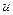– номер параллельного опыта; 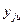– значение параметра оптимизации в 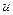-м параллельном опыте 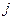-й строки матрицы.

2. Определяют дисперсию каждого опыта матрицы планирования:

. (13.15)

3. Используя 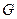– критерий Кохрена, проверяют гипотезу однородности дисперсий опытов:

. (13.16)

Дисперсии однородны, если расчётное значение – критерия не превышает табличного значения 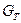– критерия (прил. 7).

4. Если дисперсии опытов однородны, то вычисляют дисперсию воспроизводимости эксперимента:

. (13.17)

5. Определяют коэффициенты уравнения регрессии:

свободный член

; (13.18)

коэффициенты регрессии, характеризующие линейные эффекты:

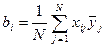; (13.19)

коэффициенты регрессии, характеризующие эффекты взаимодействия:

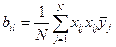, (13.20)

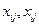где - номера факторов; - кодированные значения факторов 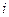и в 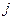-м опыте.

6. Вычислив коэффициенты регрессии, проверяют их значимость. Одним из способов является оценка с помощью -критерия Стьюдента. Расчётное значение 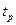критерия Стьюдента вычисляют по выражению:

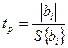, (13.21)

где - ошибка в определении 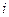–го коэффициента;

, (13.22)

где 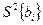- дисперсия 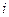–коэффициента регрессии (она одинакова для всех коэффициентов модели).

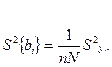(13.23)

Полученный 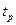-критерий сравнивают с табличным (прил. 2). Коэффициент регрессии значим, если .

Критерий Стьюдента вычисляют для каждого коэффициента регрессии. Статистически незначимые коэффициенты исключаются из уравнения регрессии.

7. Определяют дисперсию адекватности (остаточную дисперсию) , которая характеризует рассеяние эмпирических значений у относительно расчётных у, определяемых по уравнению регрессии:

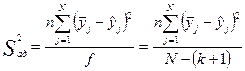, (13.24)

где 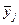– среднее арифметическое значение параметра оптимизации в -м опыте; 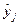– значение параметра оптимизации, вычисленное по модели для условий -го опыта; 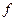– число степеней свободы равное N-(k+1), k – число факторов.

8. Проверка гипотезы адекватности найденной модели по – критерию Фишера:

. (13.25)

Табличное значение критерия отыскивается (прил. 8) по числам степеней свободы j_g = N(n-1) и j_m = N-(k +1). Условие адекватности модели > .

Поясним изложенное примером. В табл. 13.7 приведена матрица планирования ПФЭ 2³ и его результаты. Для расчёта дисперсии воспроизводимости в эксперименте проводилось равномерное дублирование наблюдений (n=2), поэтому в табл. 13.7. приведены два значения параметра оптимизации у_j и у_j. Рассчитаем средние значения параметра оптимизации для каждого опыта. Для первого опыта имеем:

у₁ = (80.23 + 81.93)/2 = 81.08,

и аналогично находим искомые значения для остальных опытов, помещая их в соответствующий столбец (см. табл. 13.7).

Далее находим y_ju = y_ju – y_j, которые для первого опыта имеют величины:

у₁₁ = 80.23 – 81.08 = -0.85; у₁₂ = 81.93 – 81.08 = 0.85.

Аналогично находим значения для остальных опытов и результаты заносим в соответствующие столбцы, как и величины ( у_j1)²=( у_j2)².

Теперь можно найти дисперсии опытов. В первом опыте имеем:

,

а остальные значения приведены в соответствующем столбце табл.13.7. Подсчитаем сумму этого столбца (она равна 5.214) и выделим в нём максимальную дисперсию S₄² = 1.620. Теперь можно найти расчётное значение критерия Кохрена:

.

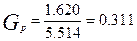Табличное значение критерия Кохрена при N = 8 и j = n –1 = 1 составляет 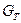= 0.7945, следовательно, можно сделать вывод о том, что дисперсии однородны (прил. 7).

Поскольку в рассматриваемом примере n_j = const = 2, дисперсию воспроизводимости находим по формуле:

.

Таблица 13.7

Матрица планирования и результаты обработки ПФЭ 2³

N	X0	X1	X2	X3	Параметр Оптимизации	∆уj1	∆yj2	(∆yj1)^2= (∆yj2)^2	Sj^2	yj	∆уj	(∆yj)^2
yj	yj	yj
	+	-	-	-	80.23	81.93	81.08	-0.85	0.85	0.722	1.444	80.88	0.2	0.040
	+	+	-	-	86.50	84.80	85.65	0.85	-0.85	0.732	1.144	85.84	-0.19	0.036
	+	-	+	-	82.45	82.10	82.27	0.18	-0.18	0.031	0.062	82.46	-0.19	0.036
	+	+	+	-	89.50	91.30	90.40	-0.90	0.90	0.810	1.620	90.22	0.18	0.032
	+	-	-	+	85.10	84.30	84.95	0.15	-0.15	0.023	0.046	84.76	0.19	0.036
	+	+	-	+	90.30	89.60	89.95	0.35	-0.35	0.123	0.246	90.16	-0.21	0.044
	+	-	+	+	85.60	84.90	85.25	0.35	-0.35	0.123	0.246	85.46	-0.21	0.044
	+	+	+	+	88.02	88.48	88.25	-0.23	0.23	0.053	0.106	88.06	0.19	0.036
å										2.607	5.214			0.304

Возникает вопрос: что делать, если дисперсии неоднородны? В этом случае надо либо отсеять выделяющиеся значения параметра оптимизации, полученные в ходе эксперимента в результате так называемых «промахов», либо, если установлено, что «промахов» допущено не было, следует увеличить число наблюдений в опыте.

Уравнение регрессии ПФЭ 2³ имеет вид:

у = b₀ + b₁x₁ + b₂x₂ + b₃x₃ + b₁₂x₁x₂ + b₁₃x₁x₃ + b₂₃x₂x₃ + b₁₂₃x₁x₂x₃.Поэтому рассчитаем коэффициенты уравнения:

b₀ = 1/8((+1)81.08+(+1)85.65+(+1)82.27+(+1)90.40+

+(+1)84.95+(+1)89.95+(+1)85.25+(+1)88.25) = 85.98

b₁ = 1/8((-1)81.08+(+1)85.65+(-1)82.27+(+1)90.40+

+(-1)84.95+(+1)89.95+(-1)85.25+(+1)88.25) = 2.59;

b₂ = 0.57, b₃ = 1.13

b₁₂ = 1/8((-1)(-1)81.08+(+1)(-1)85.65+(-1)(+1)82.27+(+1)(+1)90.4+

+(-1)(-1)84.95+(+1)(-1)89.95+(-1)(+1)85.25+(+1)(+1)88.25) = 0.20;

b₁₃ = -0.59; b₂₃ = -0.92; b₁₂₃ = -0.70.

Следовательно модель имеет следующий вид:

у = 85.98+2.59X₁+0.57X₂+1.13X₃+0.20X₁X₂–0.59X₁X₃–0.92X₂X₃-

–0.70X₁X₂X₃.

Далее нужно проверить значимость оценок коэффициентов. Найдём дисперсию оценок коэффициентов:

,

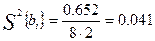и их квадратичную ошибку:

.

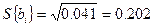Табличное значение критерия Стьюдента при доверительной вероятности 0.95 и числе степеней свободы j = N(n-1) = 8 составляет t_табл = 2.306 (прил. 2).

Вычислим расчётные значения t_p-критерия Стьюдента и сравним с t_табл:

;

t_p2 = 2.821; t_p3 = 5.594; t_p12 = 0.99; t_p13 = 2.92; t_p23 = 4.554; t₁₂₃= 3.441.

Очевидно, что все оценки, за исключением b₁₂, оказались значимыми. Тогда модель объекта будет иметь вид:

y = 85.98+2.59X₁+0.57X₂+1.13X₃–0.59X₁X₃–0.92X₂X₃–0.70X₁X₂X₃.

Далее находим дисперсию адекватности:

,

а следовательно, расчётное значение критерия Фишера:

.

Табличное значение критерия при j_g = 8 и j_m = 4 составляет (прил. 8) F_T=6.04 (при 1-L=0.95).

Расчётное значение критерия существенно меньше табличного, и следовательно, модель является адекватной.

Дата добавления: 2015-05-26