С помощью симплекс-метода 2 страница

Найдя число 160/40=4, мы тем самым с экономической точки зрения определили, какое количество изделий В предприятие может изготовлять с учетом норм расхода и имеющихся объемов сырья каждого вида. Так как сырья данного вида соответственно имеется 400, 120 и 160 кг, а на одно изделие В требуется затратить сырья каждого вида соответственно 10, 20 и 40 кг, то максимальное число изделии В, которое может быть изготовлено предприятием, равно θ₀ =min(400/10; 120/20; 160/40)=160/40=4, т.е. ограничивающим фактором для производства изделий В является имеющийся объем сырья III вида. С учетом его наличия предприятие может изготовить 4 изделия В. При этом сырье III вида будет полностью использовано.

Следовательно, вектор 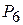подлежит исключению из базиса. Столбец вектора 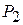и 3-я строка являются направляющими. Составляем вторую симплкс-таблицу (таблица 2.8).

Таблица 2.8. Вторая симплекс-таблица для примера 2.7

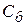
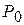
i	Базис			21	42	25	0	0	0
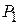
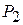
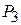
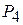
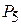
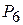
1		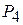		35/2					-1/4
2		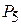		7					-1/2
3		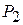		1/4		2/5			1/40
4		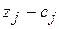	-21/2		-41/5			21/20

Сначала заполняем строку вектора, вновь введенного в базис, т. е. строку, номер которой совпадает с номером направляющей строки. Здесь направляющей является 3-я строка. Элементы этой строки таблицы 2.8 получаются из соответствующих элементов таблицы 2.7 делением их на разрешающий элемент (т.е. на 40). При этом в столбце 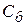записываем коэффициент 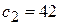, стоящий в столбце вводимого в базис вектора .

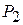Для определения остальных элементов таблицы 2.8 применяем метод исключения неизвестных Жордана-Гаусса. Затем заполняем 4-ю строку таблицы.

По окончании расчета всех элементов таблицы 2.8 в ней получены новый опорный план и коэффициенты разложения векторов 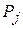(j =1,2,…,6) через базисные векторы 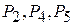и значения 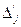и 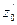. Новым опорным планом задачи является план X =(0; 4; 0; 360; 40; 0). При данном плане производства изготовляется 4 изделия В и остается неиспользованным 360 кг сырья I вида и 40 кг сырья II вида. Стоимость всей производимой при этом плане продукции равна 168 руб. Указанные числа записаны в столбце вектора P₀ таблицы 3.8. Возьмем данные столбца вектора 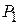. Число 1/4 в 3-й строке этого столбца показывает, на сколько следует уменьшить изготовление изделий В, если запланировать выпуск одного изделия А. Числа 35/2 и 7 в 1-й и 2-й строках вектора 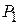показывают соответственно, сколько потребуется сырья I и II вида при включении в план производства одного изделия А, а число -21/2 в 4-й строке показывает, что если будет запланирован выпуск одного изделия А, то это обеспечит увеличение выпуска продукции в стоимостном выражении на 21/2 руб. Иными словами, если включить в план производства продукции одно изделие А, то это потребует уменьшения выпуска изделия В на 1/4 ед. и потребует дополнительных затрат 35/2 кг сырья I вида и 7 кг сырья II вида, а общая стоимость изготовляемой продукции в соответствии с новым оптимальным планом возрастет на 21/2 руб. Таким образом, числа 35/2 и 7 выступают как бы новыми «нормами» затрат сырья I и II вида на изготовление одного изделия А (как показано в таблице 2.7, ранее они были равны 20 и 12), что объясняется уменьшением выпуска изделий В.

Такой же экономический смысл имеют и данные столбца вектора 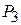таблицы 2.8. Несколько иное экономическое содержание имеют числа, записанные в столбце вектора 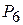. Число 1/40 в 3-й строке этого столбца, показывает, что увеличение объемов сырья III вида на 1 кг позволило бы увеличить выпуск изделий В па 1/40 ед. Одновременно потребовалось бы дополнительно 1/4 кг сырья I вида и 1/2 кг сырья II вида. Увеличение выпуска изделий В на 1/40 ед. приведет к росту выпуска продукции на 21/20 руб.

Из изложенного выше экономического содержания данных таблицы 3.8 следует, что найденный на II итерации план задачи не является оптимальным. Об этом можно судить и по 4-й строке таблицы 2.8, поскольку в столбце вектора 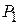этой строки стоит отрицательное число -21/2. Значит, в базис следует ввести вектор 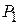, т. е. в новом плане следует предусмотреть выпуск изделий А. При определении возможного числа изготовления изделий А следует учитывать имеющееся количество сырья каждого вида, а именно: возможный выпуск изделии А определяется min (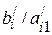), т. е. находим

θ₀ = min (360/(35/2); 40/7; 4/(1/4))=40/7.

Следовательно, исключению из базиса подлежит вектор 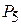, иными словами, выпуск изделий А ограничен имеющимся в распоряжении предприятия сырьем II вида. С учетом имеющихся объемов этого сырья предприятию следует изготовить 40/7 изделий А. Число 7 является разрешающим элементом, а столбец вектора 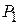и 2-я строка таблицы 3.8 являются направляющими. Составляем третью симплекс-таблицу:

Таблица 2.9. Третья симплекс-таблица для примера 2.7

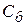
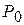
i	Базис			21	42	25	0	0	0
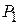
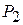
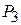
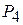
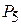
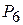
1		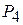				-19		-5/2
2		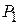	40/7			22/7		1/7	-1/14
3		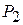	18/7			-27/70		-1/28	3/70
4		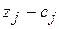			124/5		3/2	3/10

В результате в таблице 2.9 получаем новый опорный план X =(40/7; 18/7; 0; 260; 0; 0) и коэффициенты разложения векторов 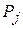(j =1,2,…,6) через базисные векторы 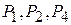и соответствующие значения 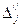и .

Т.к. в 4-ой строке таблицы 3.9 нет отрицательных чисел, то найденный опорный план является оптимальным и .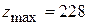

Следовательно, план выпуска продукции, включающий изготовление 40/7 изделий А и 18/7 изделии В, является оптимальным. При данном плане выпуска изделий полностью используется сырье II и III видов и остается неиспользованным 260 кг сырья I вида, а стоимость производимой продукции равна 228 руб.

Таблица 2.10. Сводная симплекс-таблица для примера 2.7

i	Базис			21	42	25	0	0	0
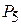
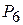
1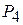
2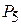
3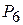
4		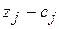	-21	-42	-25
1		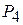		35/2					-1/4
2		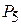							-1/2
3		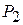		1/4		2/5			1/40
4		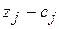	-21/2		-41/5			21/20
1		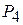				-19		-5/2
2		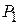	40/7			22/7		1/7	-1/14
3		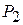	18/7			-27/70		-1/28	3/70
4		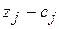			124/5		3/2	3/10

Оптимальным планом производства продукции не предусматривается изготовление изделии С. Введение в план выпуска продукции изделий вида С привело бы к уменьшению указанной общей стоимости. Это видно из 4-й строки таблицы 2.9 столбца вектора 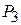, где число 124/5 показывает, что при данном плане включение в него выпуска единицы изделия С приводит лишь к уменьшению общей величины стоимости на 124/5 руб.

Решение данного примера можно было бы проводить, используя лишь одну симплекс-таблицу (таблица 2.10), в которой последовательно записаны одна за другой все три итерации вычислительного процесса.

Пример 2.8. Найти максимум функции 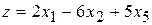при условиях

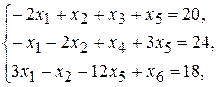
x_j 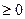(j =1,2,…,6).

Решение. Систему уравнений запишем в векторной форме:

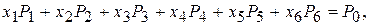
где

, , , , , , .

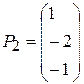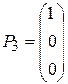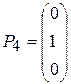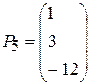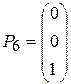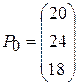Так как среди векторов 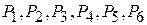имеется три единичных вектора, то для данной задачи можно непосредственно найти опорный план. Таковым является план Х =(0; 0; 20; 24; 0; 18). Составляем симплексную таблицу 2.11 и проверяем, является ли данный опорный план оптимальным.

На основе данных таблицы 2.11 делаем вывод, что исходный опорный план не является оптимальным. Поэтому переходим к новому опорному плану. Это можно сделать, так как в столбцах векторов 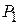и 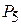4-я строка которых содержит отрицательные числа, имеются положительные элементы.

Таблица 2.11. Первая симплекс-таблица для примера 2.8

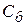
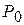
i	Базис			2	-6	0	0	5	0
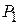
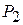
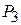
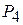
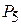
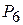
1		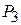		-2
2		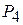		-1	-2
3		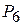			-1			-12
4		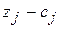	-2				-5

Для перехода к новому опорному плану введем в базис вектор 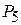и исключим из базиса вектор 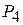. Составляем таблицу II итерации.

Таблица 2.12. Вторая симплекс-таблица для примера 2.8

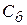
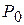
i	Базис			2	-6	0	0	5	0
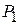
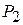
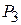
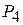
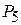
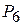
1		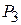		-5/3	5/3		-1/3
2		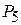		-1/3	-2/3		1/3
3		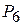		-1	-9
4		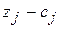	-11/3	8/3		5/3

Согласно данным таблицы 2.12, новый опорный план задачи не является оптимальным, так как в 4-й строке столбца вектора 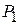стоит отрицательное число -11/3. Поскольку в столбце этого вектора нет положительных элементов, данная задача не имеет оптимального плана.

Пример 2.9. Решим с помощью симплексного метода следующую задачу линейного программирования.

Найти минимальное значение линейной функции

при ограничениях

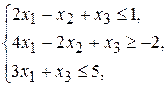
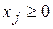(j =1,2,3).

Решение. Первоначальный опорный план рассмотренным методом находится сразу только при неотрицательных правых частях системы ограничений, поэтому умножим второе неравенство на (-1):

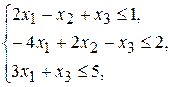
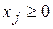(j =1,2,3).

Перейдем от неравенств к равенствам, прибавляя к левым частям неотрицательные дополнительные переменные (напомним, что дополнительным переменным в линейной функции соответствуют коэффициенты, равные нулю):

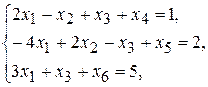
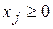(j =1,2,…,6).

Запишем систему в векторной форме:

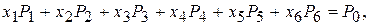
где

, , , , , , .

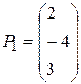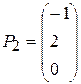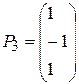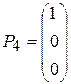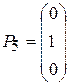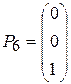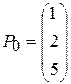Единичные векторы выберем за базис первоначального опорного плана, свободные неизвестные 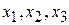приравниваем нулю. В результате получим первоначальный опорный план X =(0; 0; 0; 1; 2; 5).

Для проверки данного плана на оптимальность составляем первую симплексную таблицу (таблица 2.13) и подсчитываем значение 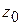и оценок 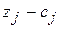. Имеем: 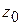=0; ; ; .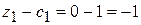

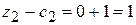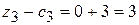Для векторов базиса оценки равны нулю. Среди полученных оценок имеются две положительные: 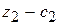=1>0; 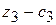=3>0. Это означает, что первоначальный опорный план не является оптимальным и его можно улучшить, включив в базис вектор 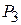, которому соответствует наибольшая положительная оценка (3).

Таблица 2.13. Первая симплекс-таблица для примера 2.9

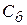
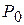
i	Базис			1	-1	-3	0	0	0
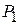
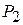
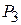
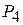
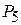
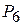
1		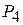			-1
2		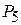		-4		-1
3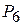
4		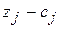	-1

Для того, чтобы определить какой вектор нужно исключить из базиса, найдем θ₀ = min (1/1; 5/1)=1/1=1. Таким образом, разрешающим элементом является число 1, стоящее на пересечении первой строки и третьего столбца, первая строка и третий столбец являются направляющими; необходимо вектор 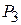включить в базис, а вектор 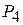исключить.

Составим вторую симплексную таблицу (таблица 2.14).

Таблица 2.14. Вторая симплекс-таблица для примера 2.9

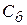
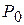
i	Базис			1	-1	-3	0	0	0
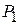
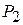
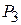
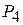
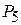
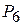
1		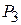-3			-1
2		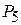		-2
3		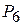					-1
4		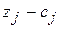-3	-7			-3

Дата добавления: 2015-05-26