
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
С помощью симплекс-метода 1 страница
|
|
|
|
Методика решения задач линейной оптимизации
Оптимизации
Симплекс-метод решения задач линейной
Лабораторная работа № 1
Задания №№ 1-10. Построить на плоскости область решений линейных неравенств и геометрически найти максимальное и минимальное значения целевой функции в этой области.
1. 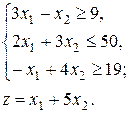 2.
2. 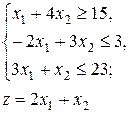
3. 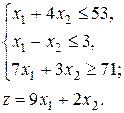 4.
4. 
5. 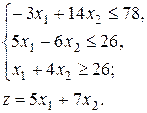 6.
6. 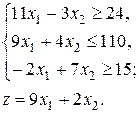
7. 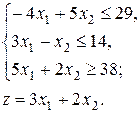 8.
8. 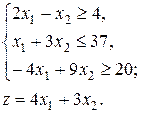
9. 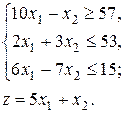 10.
10. 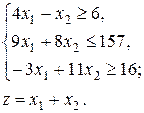
Симплекс-метод предназначен для решения канонической задачи линейного программирования.
Итак, рассмотрим задачу линейного программирования с ограничениями в форме уравнений. Дана система ограничений
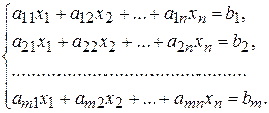 (2.25)
(2.25)
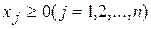 ,
, 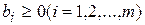 (2.26)
(2.26)
и целевая функция
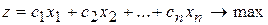 . (2.27)
. (2.27)
Для начала работы по симплекс-методу требуется, чтобы заданная система уравнений была приведена к допустимому виду. Это означает, что какие-то из неизвестных должны быть выражены через остальные, причем свободные члены этих выражений неотрицательны.
Пример 2.6. Рассмотрим пример допустимой системы:
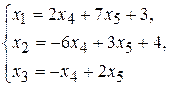
Здесь свободные члены равны соответственно 3, 4, 0.
После того как выделен допустимый базис неизвестных, можно в выражении для целевой функции заменить каждое базисное неизвестное его выражением через свободные неизвестные.
Симплексный метод решения задачи линейного программирования основан на переходе от одного опорного плана к другому, при котором значение целевой функции возрастает (при условии, что данная задача имеет оптимальный план и каждый ее опорный план является невырожденным). Указанный переход возможен, если известен какой-нибудь исходный опорный план. Рассмотрим задачу, для которой этот план можно непосредственно записать.
Пусть требуется найти максимальное значение функции
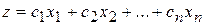
при условиях
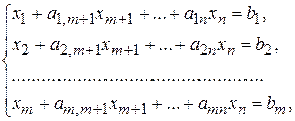 (2.28)
(2.28)
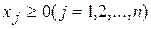 .
.
Здесь 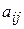 ,
, 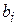 и
и 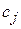 (i =1,2,…, m; j =1,2,…, n) – заданные постоянные числа, причем
(i =1,2,…, m; j =1,2,…, n) – заданные постоянные числа, причем 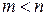 и
и 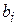 > 0.
> 0.
|
|
|
Векторная форма данной задачи имеет следующий вид: найти максимум функции
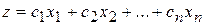
при условиях
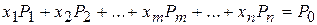 , (2.29)
, (2.29)
где
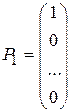 ,
, 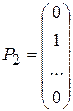 ,…,
,…, 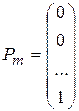 ,
,
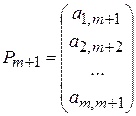 ,…,
,…, 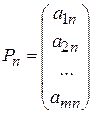 ,
, 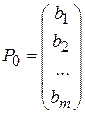 .
.
Т.к.  то план X =(
то план X =(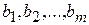 , 0, …, 0) является опорным планом данной задачи. Этот план определяется системой единичных векторов
, 0, …, 0) является опорным планом данной задачи. Этот план определяется системой единичных векторов 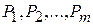 , которые образуют базис m -мерного пространства. Поэтому каждый из векторов
, которые образуют базис m -мерного пространства. Поэтому каждый из векторов 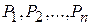 , а также вектор
, а также вектор 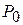 могут быть представлены в виде линейной комбинации векторов данного базиса. Пусть
могут быть представлены в виде линейной комбинации векторов данного базиса. Пусть
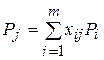 (j =0, 1,…, n).
(j =0, 1,…, n).
Положим 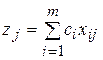 ;
;  .
.
Т.к. векторы P1, P2,…, Pm – единичные, то 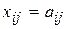 и
и 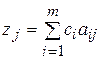 , а
, а 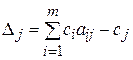 .
.
Теорема 2.2 (признак оптимальности опорного плана). Опорный план X =(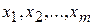 , 0, …, 0) является оптимальным, если
, 0, …, 0) является оптимальным, если 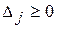 для любого j (j =1, 2,…, n).
для любого j (j =1, 2,…, n).
Замечание. Если требуется найти минимальное значение, которое принимает целевая функция, то опорный план X =(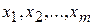 , 0, …, 0) будет являться оптимальным, если
, 0, …, 0) будет являться оптимальным, если 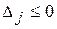 для любого j (j =1, 2,…, n).
для любого j (j =1, 2,…, n).
Теорема 2.3. Если 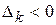 для некоторого j=k и среди чисел
для некоторого j=k и среди чисел 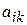 нет положительных, то целевая функция не ограничена на множестве ее планов.
нет положительных, то целевая функция не ограничена на множестве ее планов.
Замечание. В задаче на минимум если 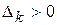 для некоторого j=k и среди чисел
для некоторого j=k и среди чисел 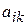 нет положительных, то целевая функция не ограничена на множестве ее планов.
нет положительных, то целевая функция не ограничена на множестве ее планов.
Теорема 2.4. Если опорный план X не вырожден и 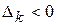 , но среди чисел
, но среди чисел 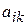 есть положительные, то существует опорный план X* такой, что
есть положительные, то существует опорный план X* такой, что 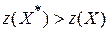 .
.
Замечание. В задаче на отыскание минимального значения целевой функции если опорный план X не вырожден и 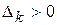 , но среди чисел
, но среди чисел 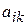 есть положительные, то существует опорный план X* такой, что
есть положительные, то существует опорный план X* такой, что 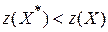 .
.
Сформулированные теоремы позволяют проверить, является ли найденный опорный план оптимальным, и выявить целесообразность перехода к новому опорному плану.
Исследование опорного плана на оптимальность, а также дальнейший вычислительный процесс удобнее вести, если условия задачи и первоначальные данные, полученные после определения исходного опорного плана, записать так, как показано в таблице 2.5.
Таблица 2.5. Симплекс-таблица
| i | Базис | 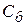
| 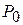
| 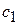
| 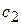
| … | 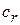
| … | 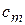
| 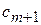
| … | 
| … | 
|
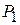
| 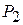
| … | 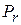
| … | 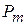
| 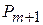
| … | 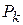
| … | 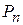
| ||||
| 1 | 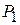
| 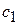
| 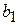
| … | … | 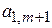
| … | 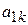
| ... | 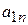
| ||||
| 2 | 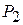
| 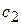
| 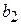
| … | … | 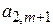
| … | 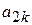
| … | 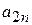
| ||||
| … | … | … | … | … | … | … | … | … | … | … | … | … | … | … |
| r | 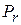
| 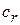
| 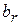
| … | … | 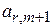
| … | 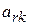
| … | 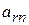
| ||||
| … | … | … | … | … | … | … | … | … | … | … | … | … | … | … |
| m | 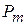
| 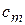
| 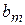
| … | … | 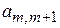
| … | 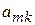
| … | 
| ||||
| m+1 | 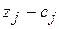
| 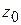
| … | … | 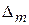
| … | 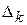
| … | 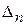
|
|
|
|
В таблице 3.5 первые m строк определяются исходными данными задачи, а показатели (m +1)-й строки вычисляют. В этой строке в столбце вектора 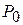 записывают значение целевой функции, которое она принимает при данном опорном плане, а в столбце вектора
записывают значение целевой функции, которое она принимает при данном опорном плане, а в столбце вектора 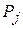 -значение
-значение  .
.
Значение 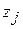 находится как скалярное произведение вектора
находится как скалярное произведение вектора 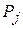 (j =1,2,…, m) на вектор
(j =1,2,…, m) на вектор 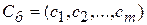 :
:
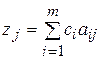 .
.
Значение z0 равно скалярному произведению вектора P0 на вектор 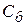 :
:
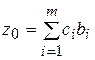 .
.
После заполнения таблицы 3.5 исходный опорный план проверяют на оптимальность. Для этого просматривают элементы (m+1)-й строки таблицы. В результате может иметь место один из следующих трех случаев:
1) 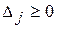 для j = m+ 1, m+ 2,…, n (j =1,2,…, m,
для j = m+ 1, m+ 2,…, n (j =1,2,…, m,  ). Поэтому в данном случае числа
). Поэтому в данном случае числа 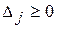 для всех j от 1 до n;
для всех j от 1 до n;
2) 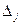 <0 для некоторого j, и все соответствующие этому индексу величины
<0 для некоторого j, и все соответствующие этому индексу величины 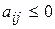 (i =1,2,…, m);
(i =1,2,…, m);
3) 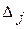 <0 для некоторых индексов j, и для каждого такого j по крайней мере одно из чисел
<0 для некоторых индексов j, и для каждого такого j по крайней мере одно из чисел 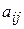 положительно.
положительно.
В первом случае на основании признака оптимальности исходный опорный план является оптимальным. Во втором случае целевая функция не ограничена сверху на множестве планов, а в третьем случае можно перейти от исходного плана к новому опорному плану, при котором значение целевой функции увеличится. Этот переход от одного опорного плана к другому осуществляется исключением из исходного базиса какого-нибудь из векторов и введением в него нового вектора. В качестве вектора, вводимого в базис, можно взять любой из векторов 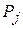 , имеющий индекс j, для которого
, имеющий индекс j, для которого 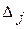 <0. Пусть, например,
<0. Пусть, например, 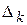 <0 и решено ввести в базис вектор
<0 и решено ввести в базис вектор 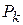 .
.
Для определения вектора, подлежащего исключению из базиса, находят 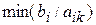 для всех
для всех 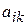 >0. Пусть этот минимум достигается при i=r. Тогда из базиса исключают вектор
>0. Пусть этот минимум достигается при i=r. Тогда из базиса исключают вектор 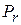 , а число
, а число 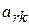 называют разрешающим элементом.
называют разрешающим элементом.
Замечание. C целью упрощения вычислительного процесса в дальнейшем будем вектор, вводимый в базис, определять, исходя из максимальной абсолютной величины отрицательных чисел 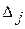 . Если же таких чисел несколько, то в базис будем вводить вектор, имеющий такой же индекс, как и максимальное из чисел
. Если же таких чисел несколько, то в базис будем вводить вектор, имеющий такой же индекс, как и максимальное из чисел 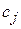 , определяемых данными числами
, определяемых данными числами 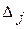 (
(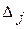 <0).
<0).
|
|
|
Столбец и строку, на пересечении которых находится разрешающий элемент, называют направляющими.
После выделения направляющей строки и направляющего столбца находят новый опорный план и коэффициенты разложения векторов 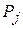 через векторы нового базиса, соответствующего новому опорному плану. Это легко реализовать, если воспользоваться методом Жордана - Гаусса.
через векторы нового базиса, соответствующего новому опорному плану. Это легко реализовать, если воспользоваться методом Жордана - Гаусса.
После вычисления 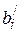 и
и 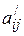 их значения заносят в следующую таблицу (II итерация).
их значения заносят в следующую таблицу (II итерация).
После заполнения новой симплекс-таблицы просматривают элементы (m +1) - й строки. Если все 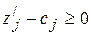 , то новый опорный план является оптимальным. Если же среди указанных чисел имеются отрицательные, то находят новый опорный план. Этот процесс продолжают до тех нор, пока либо не получают оптимальный план задачи, либо не устанавливают ее неразрешимость.
, то новый опорный план является оптимальным. Если же среди указанных чисел имеются отрицательные, то находят новый опорный план. Этот процесс продолжают до тех нор, пока либо не получают оптимальный план задачи, либо не устанавливают ее неразрешимость.
Пример 2.7. Для изготовления различных изделий А, В и С предприятие использует три различных вида сырья. Нормы расхода сырья на производство одного изделия каждого вида, цена одного изделия А, В и С, а также общее количество сырья каждого вида, которое может быть использовано предприятием, приведены в таблице 3.6.
Таблица 2.6. Исходные данные для примера 2.7
| Вид сырья | Нормы затрат сырья (кг) на одно изделие | Общее количество сырья (кг) | ||
| A | В | С | ||
| I | ||||
| II | ||||
| III | ||||
| Цена одного изделия (руб.) |
Изделия А, В и С могут производиться в любых соотношениях (сбыт обеспечен), но производство ограничено выделенным предприятию сырьем каждого вида.
Составить план производства изделий, при котором общая стоимость всей произведенной предприятием продукции является максимальной.
Решение. Составим математическую модель задачи. Искомый выпуск изделий А обозначим через 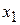 , изделий В - через
, изделий В - через 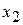 , изделий С - через
, изделий С - через 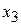 . Поскольку имеются ограничения на выделенный предприятию фонд сырья каждого вида, переменные
. Поскольку имеются ограничения на выделенный предприятию фонд сырья каждого вида, переменные 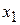 ,
, 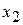 ,
, 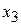 должны удовлетворять следующей системе неравенств:
должны удовлетворять следующей системе неравенств:
|
|
|
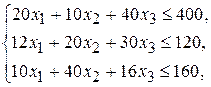 (2.30)
(2.30)
Общая стоимость произведенной предприятием продукции при условии выпуска 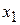 изделий А,
изделий А, 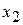 изделий В и
изделий В и 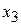 изделий С составляет
изделий С составляет
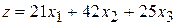 . (2.31)
. (2.31)
По своему экономическому содержанию переменные 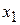 ,
, 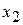 ,
, 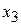 могут принимать только лишь неотрицательные значения:
могут принимать только лишь неотрицательные значения:
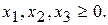 (2.32)
(2.32)
Таким образом, приходим к следующей математической задаче: среди всех неотрицательных решений системы неравенств (2.30) требуется найти
такое, при котором функция (2.31) принимает максимальное значение.
Запишем эту задачу в форме основной задачи линейного программирования. Для этого перейдем от ограничений-неравенств к ограничениям-равенствам. Введем три дополнительные переменные, в результате чего ограничения запишутся в виде системы уравнений
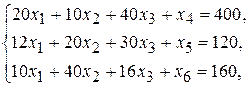
Эти дополнительные переменные по экономическому смыслу означают не используемое при данном плане производства количество сырья того или иного вида. Например, 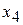 - это неиспользуемое количество сырья I вида.
- это неиспользуемое количество сырья I вида.
Преобразованную систему уравнений запишем в векторной форме:
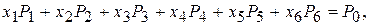
где
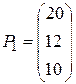 ,
, 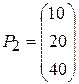 ,
,  ,
, 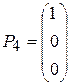 ,
, 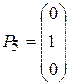 ,
, 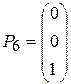 ,
, 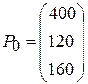 .
.
Поскольку среди данных векторов имеются три единичных вектора, для данной задачи можно непосредственно записать опорный план. Таковым является план X =(0; 0; 0; 400; 120; 160), определяемый системой трехмерных единичных векторов  , которые образуют базис трехмерного векторного пространства.
, которые образуют базис трехмерного векторного пространства.
Составляем симплексную таблицу (таблица 3.7), подсчитываем значения 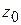 ,
, 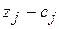 и проверяем исходный опорный план на оптимальность:
и проверяем исходный опорный план на оптимальность:
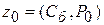 =
= 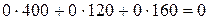 ;
;  =
= 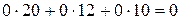 ;
;
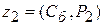 =
= 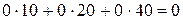 ;
;
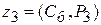 =
= 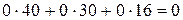 ;
;
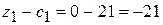 ;
; 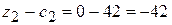 ;
; 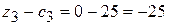 .
.
Для векторов базиса 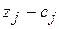 =0.
=0.
Таблица 2.7. Первая симплекс-таблица для примера 2.7
| i | Базис | 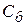
| 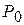
| 21 | 42 | 25 | 0 | 0 | 0 |
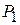
| 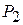
| 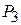
| 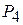
| 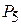
| 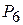
| ||||
| 1 | 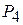
| ||||||||
| 2 | 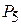
| ||||||||
| 3 | 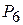
| 40 | |||||||
| 4 | 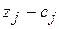
| -21 | -42 | -25 |
Согласно данным таблицы 2.7, значения всех основных переменных 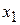 ,
, 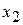 ,
, 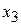 равны нулю, а дополнительные переменные принимают свои значения в соответствии с ограничениями задачи. Эти значения переменных отвечают такому «плану», при котором ничего не производится, сырье не используется и значение целевой функции равно нулю (т.е. стоимость произведенной продукции отсутствует).
равны нулю, а дополнительные переменные принимают свои значения в соответствии с ограничениями задачи. Эти значения переменных отвечают такому «плану», при котором ничего не производится, сырье не используется и значение целевой функции равно нулю (т.е. стоимость произведенной продукции отсутствует).
Данный план не является оптимальным, т.к. в 4-й строке таблицы 2.7 имеется три отрицательных числа: -21, -42, -25. Отрицательные числа не только свидетельствуют о возможности увеличения общей стоимости производимой продукции, но и показывают, на сколько увеличится эта сумма при введении в план единицы того или другого вида продукции.
Так, число -21 означает, что при включении в план производства одного изделия А обеспечивается увеличение выпуска продукции на 21 руб. Если включить в план производства по одному изделию В и С, то общая стоимость изготовляемой продукции возрастет соответственно на 42 и 25 руб. Поэтому с экономической точки зрения наиболее целесообразным является включение в план производства изделий В. Это же необходимо сделать и на основании формального признака симплексного метода, поскольку максимальное по абсолютной величине отрицательное число 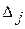 стоит в 4-й строке столбца вектора
стоит в 4-й строке столбца вектора 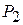 . Следовательно, в базис введем вектор
. Следовательно, в базис введем вектор 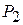 . Определяем вектор, подлежащий исключению из базиса. Для этого находим θ0 =
. Определяем вектор, подлежащий исключению из базиса. Для этого находим θ0 = 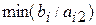 для
для 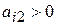 , т. е. θ0 =min(400/10; 120/20; 160/40)=160/40=4.
, т. е. θ0 =min(400/10; 120/20; 160/40)=160/40=4.
|
|
|
|
|
Дата добавления: 2015-05-26; Просмотров: 641; Нарушение авторских прав?; Мы поможем в написании вашей работы!