
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Программирования
|
|
|
|
Общая и основная задачи линейного
Общей задачей линейного программирования называется задача, которая состоит в определении максимального (минимального) значения функции
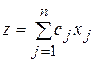 (2.8)
(2.8)
при условиях
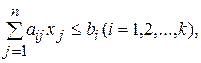 (2.9)
(2.9)
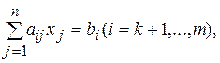 (2.10)
(2.10)
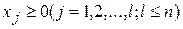 . (2.11)
. (2.11)
где 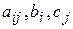 - заданные постоянные величины и
- заданные постоянные величины и 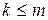 .
.
Функция (2.8) называется целевой функцией (линейной формой) задачи (2.8)-(2.11), а условия (2.9)-(2.11) – ограничениями данной задачи.
Стандартной (симметричной) задачей линейного программирования называется задача, которая состоит в определении максимального значения функции (2.8) при условиях (2.9) и (2.11), где k=m и l=n.
Канонической (основной) задачей линейного программирования называется задача, которая состоит в определении максимального значения функции (2.8) при условиях (2.10) и (2.11), где k= 0 и l=n.
Совокупность чисел 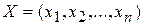 , удовлетворяющих ограничениям (2.9)-(2.11), называется допустимым решением (планом).
, удовлетворяющих ограничениям (2.9)-(2.11), называется допустимым решением (планом).
План 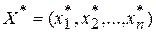 , при котором целевая функция (2.8) принимает свое максимальное (минимальное) значение, называется оптимальным.
, при котором целевая функция (2.8) принимает свое максимальное (минимальное) значение, называется оптимальным.
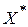 - оптимальный план задачи, если
- оптимальный план задачи, если 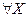
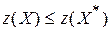 (в задаче на максимум) и
(в задаче на максимум) и 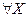
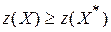 (в задаче на минимум).
(в задаче на минимум).
Замечание. Все 3 формы задачи линейного программирования эквивалентны:
1) Если требуется найти минимум функции
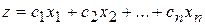 ,
,
можно перейти к нахождению максимума функции
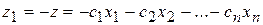 ,
,
т.к. min z=-max(-z).
2) От знака «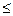 » в ограничениях можно перейти к «=» добавлением к левой части ограничения дополнительной переменной, а от знака «
» в ограничениях можно перейти к «=» добавлением к левой части ограничения дополнительной переменной, а от знака «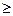 » - вычитанием дополнительной неотрицательной переменной.
» - вычитанием дополнительной неотрицательной переменной.
3) Число вводимых дополнительных переменных равно числу преобразуемых неравенств.
Пример 2.1. Записать в форме основной задачи линейного программирования следующую задачу: найти максимум функции
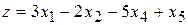 (2.12)
(2.12)
при условиях
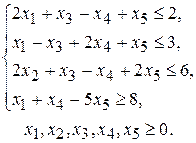 (2.13)
(2.13)
Решение. Чтобы записать в форме основной задачи нужно перейти к ограничениям-равенствам:
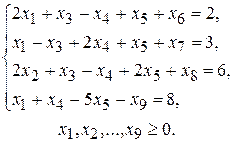 (2.14)
(2.14)
Данная задача может быть записана в форме основной таким образом: максимизировать функцию (2.12) при условиях (2.14).
Пример 2.2. Записать задачу, состоящую в минимизации функции
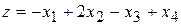 (2.15)
(2.15)
при условиях
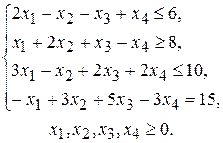 (2.16)
(2.16)
в форме основной задачи линейного программирования.
Решение. Вместо нахождения минимума функции z нужно найти максимум функции 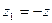 при ограничениях, получающихся из исходных добавлением к левым частям неравенств «
при ограничениях, получающихся из исходных добавлением к левым частям неравенств «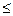 », и вычитанием из левых частей неравенств со знаком «
», и вычитанием из левых частей неравенств со знаком «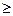 » дополнительных переменных. Тогда исходная задача может быть записана в форме основной задачи линейного программирования так:
» дополнительных переменных. Тогда исходная задача может быть записана в форме основной задачи линейного программирования так:
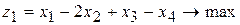
при условиях
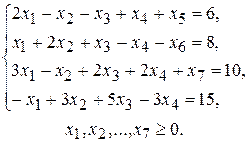
Пример 2.3. Записать следующую задачу в стандартной форме линейного программирования: найти максимум функции
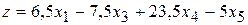 (2.17)
(2.17)
при условиях
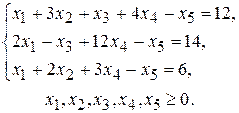 (2.18)
(2.18)
Решение. Выпишем расширенную матрицу системы и с помощью метода исключения неизвестных Жордана-Гаусса приведем ее к ступенчатой форме:
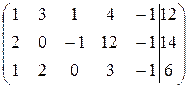 ~
~ 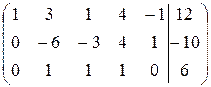 ~
~ 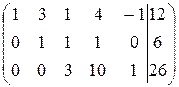 ~
~ 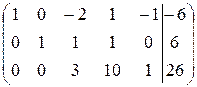 ~
~ 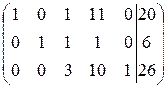 .
.
Таким образом, исходную систему мы свели к следующей:
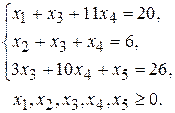
Выразим 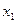 и
и 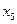 через
через 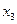 и
и 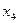 и подставим в z
и подставим в z
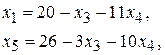
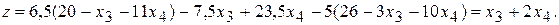
Тогда задача будет состоять в нахождении максимального значения функции
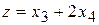
при условиях
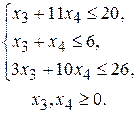
Замечание. Вводимые дополнительные переменные имеют вполне экономический смысл. Так, если в ограничениях исходной задачи отражается расход и наличие производственных ресурсов, то числовое значение дополнительной переменной в плане задачи, записанной в форме основной, равно объему неиспользуемого соответствующего ресурса.
|
|
|
|
|
Дата добавления: 2015-05-26; Просмотров: 372; Нарушение авторских прав?; Мы поможем в написании вашей работы!